1. Analiza Fouriera

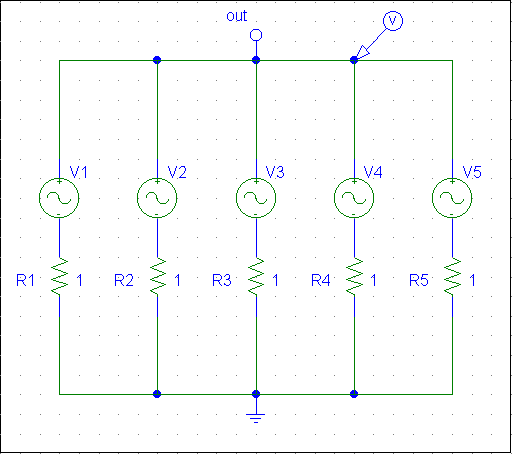
1. W układzie jak na rysunku mierzymy napięcie na wyjściu , zadając w

parametrach źródła te same wartości amplitudy , przy czym wartość

częstotliwości każdego kolejnego źródła jest wielokrotnością

częstotliwości 50 Hz :

Wyniki obliczeń programu analizującego :

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(out)

DC COMPONENT = 1.070982E-06

HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED

NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)

1 5.000E+01 1.000E+01 1.000E+00 1.195E-05 0.000E+00

2 1.000E+02 1.000E+01 1.000E+00 1.281E-05 -1.110E-05

3 1.500E+02 1.000E+01 1.000E+00 1.283E-05 -2.303E-05

4 2.000E+02 1.000E+01 1.000E+00 8.647E-06 -3.916E-05

5 2.500E+02 1.000E+01 1.000E+00 -5.589E-06 -6.535E-05

TOTAL HARMONIC DISTORTION = 1.999970E+02 PERCENT

JOB CONCLUDED

TOTAL JOB TIME 1.07

Wyniki otrzymane z programu porównujemy z wartościami

zadanymi do analizy oczekując że będą one zgodne.

Wykres uzyskany z symulacji powyższego układu przedstawiony jest

jako „wykres 1 - analiza Fouriera dla tych samych wartoÅ›ci amplitudy”

2. W tym samym układzie co powyżej przeprowadzamy symulację dla różnych wartości amplitudy źródeł zasilających .

Wyniki obliczeń programu analizującego :

FOURIER COMPONENTS OF TRANSIENT RESPONSE V(out)

DC COMPONENT = 3.053222E-06

HARMONIC FREQUENCY FOURIER NORMALIZED PHASE NORMALIZED

NO (HZ) COMPONENT COMPONENT (DEG) PHASE (DEG)

1 5.000E+01 4.000E-01 1.000E+00 1.001E-03 0.000E+00

2 1.000E+02 1.000E+01 2.500E+01 5.670E-05 -1.945E-03

3 1.500E+02 1.000E+02 2.500E+02 2.402E-06 -3.000E-03

4 2.000E+02 2.000E+01 5.000E+01 -1.014E-05 -4.013E-03

5 2.500E+02 1.000E+01 2.500E+01 -2.225E-05 -5.025E-03

TOTAL HARMONIC DISTORTION = 2.573876E+04 PERCENT

JOB CONCLUDED

TOTAL JOB TIME .90

Wykres z powyższej symulacji przedstawiony jest jako „wykres 2 -

analiza Fouriera dla różnych wartoÅ›ci amplitudy”

2. Analiza FFT

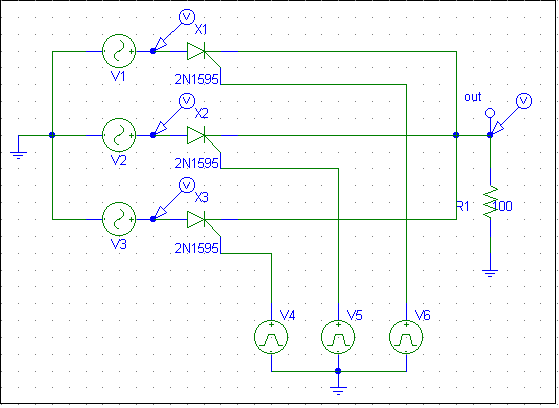
1. W układzie jak na rysunku dla prostownika tyrystorowego

trójpulsowego mierzymy napięcie wyjściowe . Parametry analizy i

źródeł sterujących są tak ustawione aby tyrystory były załączane po

pierwszej ćwiartce przebiegu wejściowego .

Wykres z powyższej symulacji przedstawiony jest jako

„wykres 3 - analiza FFT ”.

2. W tym samym układzie zmieniamy parametr TD w źródłach

sterowanych VPULSE.

Wykres z tej symulacji przedstawiony jest jako

„wykres 4 - analiza FFT ”.

3. Korzystając z tego samego układu zmieniamy parametr V1 w

źródłach sterowanych VPULSE.

Wykres z tej symulacji przedstawiony jest jako

„wykres 5 - analiza FFT ”.

3. Wnioski:

• w analizie Fouriera przy zadanej amplitudzie którÄ… możemy nazwać

amplitudą odniesienia , podczas symulacji wyniki pomiarów są

odnoszone do tejże wÅ‚aÅ›nie amplitudy np. tak jak widać to w „tabelce”

powyżej , gdy na źródle ustawimy amplitudę 2 , a w parametrach analizy

50 (amplituda odniesienia) to w wynikach obliczeń dla tego źródła

otrzymamy 0,4

• zmieniajÄ…c parametr TD źródeÅ‚ sterowanych powodujemy że tyrystory

wyzwalane są nieco później niż po ćwiartce przebiegu wejściowego

• zmiana z kolei parametru V1 źródeÅ‚ powoduje wczeÅ›niejsze wyzwalanie

tyrystorów

---