1. Przykłady zastosowań modeli decyzyjnych w działalności przedsiębiorstwa

Modele decyzyjne w przygotowaniu działalności przedsiębiorstwa

• strategia wyboru produktu (co wytwarzać)

• strategia wyboru technologii (ile produkować)

• strategia wyboru miejsca lokalizacji (gdzie wytwarzać)

• strategia rozmieszczenia obiektów

• strategia organizacji zaopatrzenia (niezbędne czynniki produkcji i ich ilość)

• strategia wykorzystania czynnika ludzkiego

Modele decyzyjne w planowaniu działalności produkcyjnej przedsiębiorstwa:

• problem przydziału zadań w czasie

• problem harmonogramowania zadań na urządzeniach

• problem planowania i kontroli przedsięwzięć złożonych z wielu zadań elementarnych

Modele decyzyjne w planowaniu działalności marketingowej

Modele decyzyjne w planowaniu działalności finansowej przedsiębiorstwa

2. Cechy metody badań operacyjnych

• ukierunkowanie na podejmowanie decyzji

• interdyscyplinarny charakter badań operacyjnych - konieczność tworzenia zespołów specjalistów z wielu dziedzin w celu formułowania i rozwiązywania modeli badań operacyjnych

• podejmowanie decyzji na podstawie modelu analizowanych systemów, a nie bezpośrednio na podstawie analizy systemów

• konieczność budowy modelu decyzyjnego i eksperymentowanie na nim według określonych reguł

• lepsze poznanie procesu decyzyjnego i jego specyfiki dzięki metodzie budowy modelu decyzyjnego

• konieczność wykorzystywania techniki komputerowej

3. Etapy procedury rozwiązującej problemy decyzyjne za pomocą badań operacyjnych

• rozpoznanie sytuacji decyzyjnej i wynikającego z niej problemu decyzyjnego

• budowa modelu decyzyjnego

• rozwiązanie modelu decyzyjnego

• ocena poprawności i weryfikacja modelu

• przygotowaniu decyzji i opracowanie systemu kontroli realizacji

4. Rodzaje modeli decyzyjnych

• model konceptualny

• model formalny (matematyczny)

• model optymalizacyjny

• model komputerowy

5. Klasyfikacja modeli decyzyjnych

• według liczby kryteriów (jednokryteriowe, wielokryteriowe)

• według postaci funkcji celu i ograniczeń (liniowe, nieliniowe)

• według postaci zmiennych decyzyjnych (ciągłe, dyskretne)

• według charakteru parametrów modelu (deterministyczne, stochastyczne)

• według liczby etapów opisu procesu decyzyjnego

6. Działy badań operacyjnych

• programowanie liniowe, optymalizacja dyskretna

• zagadnienie transportowe

• programowanie wielokryterialne

• programowanie dynamiczne

• teoria grafów i sieci

• teoria gier strategicznych

• teoria masowej obsługi

• modele decyzyjne gospodarki zapasami

7. Układ wektorów liniowo niezależnych, liniowo zależnych

• układ wektorów jest liniowo zależny, jeżeli chociaż jeden z nich jest kombinacją pozostałych

• w układzie wektorów niezależnych żadnego z tych wektorów nie można przedstawić jako kombinacji liniowej pozostałych

8. Czy wektory jednostkowe tworzą układ wektorów liniowo zależny, czy liniowo niezależny?

Wektory jednostkowe w przestrzeni Rⁿ stanowią układ liniowo niezależny

9. Liczba wektorów liniowo niezależnych w przestrzeni n-wymiarowej

Maksymalna liczba liniowo niezależnych wektorów w przestrzeni Rⁿ wynosi n.

10. Baza zbioru, liczność wektorów liniowo niezależnych, tworzących bazę.

• bazą zbioru S nazywamy liniowo niezależny układ wektorów b₁..b_k należących do S, rozpinający zbiór S

• liczba wektorów stanowiących bazę zbioru S jest równa maksymalnej liczbie wektorów liniowo niezależnych należących do S.

11. Czy dowolny element zbioru można przedstawić w sposób jednoznaczny jako kombinację liniową wektorów bazowych tego zbioru?

Dla ustalonej bazy B zbioru S dowolny element a należący do S można przedstawić w sposób jednoznaczny jako kombinację liniową wektorów bazy.

12. Rozwiązanie bazowe układu równań

• rozwiązaniem bazowym układu równań nazywamy takie rozwiązanie x(B) należące do Rⁿ w którym wszystkie zmienne niebazowe są równe zeru (xR=0)

13. Wartości zmiennych niebazowych w rozwiązaniu bazowym

• jw. = 0

14. Rozwiązanie bazowe zdegenerowane

• rozwiązanie bazowe nazywamy zdegenerowanym, jeżeli chociaż jedna ze składowych części bazowej (tzn. x_B) jest równa 0

15. Maksymalna liczba rozwiązań bazowych układu równań o macierzy m x n.

• maksymalna liczba rozwiązań bazowych układu Ax = b, w którym A jest typu mx n, r (A) =m, m<=n, wynosi
  

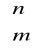
• m równań, n niewiadomych

16. Postać klasyczna zadania programowania liniowego

• postać f-ji celu:
  

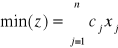
• warunki ograniczające:
  

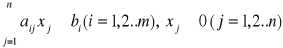
• gdzie:

• (x₁, x₂...x_n) należące do Rⁿ - wektor zmiennych decyzyjnych

• z należące do R - wartość f-ji celu

• (c₁...c_n) należące do Rⁿ - wektor kosztów (cen jednostkowych) ?????????????

• A = |a_ij| macierz współczynników nakładów

• B = |b_i| wektor ograniczeń nakładów

17. Postać standardowa zdania programowania liniowego

• postać f-ji celu:
  

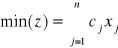
• warunki ograniczające:
  

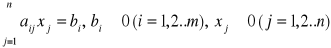
• gdzie:

• (x₁, x₂...x_n) należące do Rⁿ - wektor zmiennych decyzyjnych

• z należące do R - wartość f-ji celu

• (c₁...c_n) należące do Rⁿ - wektor kosztów (cen jednostkowych) ??????

• A = |a_ij| macierz współczynników nakładów

• B = |b_i| wektor ograniczeń nakładów

18. Rozwiązanie dopuszczalne zadania programowania liniowego

• dowolny wektor spełniający warunki ograniczające

19. Rozwiązanie bazowe zadania programowania liniowego

• jw. - wszystkie zmienne niebazowe = 0

• jeśli dla każdego
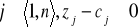
  , to takie rozwiązanie nazywamy optymalnym

20. Rozwiązanie optymalne zadania programowania liniowego

• dla dowolnego rozwiązania dopuszczalnego x_o jeśli x<>x₀ f(x)<=f(x₀) ???????????

• ich ilość może być >1, może ich nie być w ogóle (nieograniczona wartość f-cji celu)

21. Kiedy zadanie programowania liniowego nazywamy sprzecznym

• kiedy zadanie nie ma rozwiązań dopuszczalnych (metoda simpleks: w rozwiązaniu optymalnym występują niezerowe zmienne sztuczne)

22. Liczba zmiennych bazowych rozwiązania bazowego dopuszczalnego zadania programowania liniowego

• il. warunków ograniczających?

23. Zbiory wypukłe, wierzchołki zbioru wypukłego

• zbiór C należący do Rⁿ nazywamy wypukłym, jeżeli dla dowolnych x₁,x₂ należących do C oraz dla dowolnego 0<=λ<=1 zachodzi: (λ *x₁ + (1 - λ)*x₂) należy do C.

Wierzchołkiem zbioru wypukłego nazywamy p-t, dla którego nie istnieją dwa różne p-ty x₁<> x₂<>x, że x=ax₁+(1-a)x₂

24. Jaki zbiór w przestrzeni (interpretacja geometryczna) tworzy zbiór rozwiązań dopuszczalnych zadania programowego liniowego?

• figura geometryczne zawarta między wykresami funkcji ograniczających - może być zbiorem pustym lub być nieograniczona ZBIÓR WYPUKŁY

25. Gdzie w zbiorze rozwiązań dopuszczalnych zadania programowania liniowego znajdują się rozwiązania bazowe dopuszczalne?

• Jest punktem wierzchołkowym zbioru rozwiązań dopuszczalnych.

26. Gdzie w przestrzeni należy poszukiwać rozwiązania optymalnego zadania programowania liniowego?

• Rozwiązań optymalnych zadania programowania liniowego należy szukać wśród dopuszczalnych rozwiązań bazowych układu ograniczeń. (w wierzchołkach zbioru rozwiązań dopuszczalnych)

27. Liczba rozwiązań optymalnych zadania programowania liniowego.

• zero - zadanie sprzeczne

• 1

• wiele

• brak skończonego rozwiązania optymalnego

28. Zmienne osłabiające w zadaniach programowania liniowego

• Zmienne osłabiające (bilansujące) służą do usunięcia nierówności < (dodanie zmiennej) lub > (odjęcie zmiennej) w ograniczeniach ZPL (podczas doprowadzania do postaci standardowej)

• postać standardową uzyskuje się poprzez wprowadzenie zmiennych osłabiających (wektora zmiennych dodatkowych)

• Ax+x^d=b, b>=0

• X>=0, x^d>=0

Wtedy początkowym rozwiązaniem bazowym jest: x=0, x^d=b ???????????????????????????????

29. Zmienne sztucznej bazy w zadaniach programowania liniowego

• są to sztuczne wektory jednostkowe, dodawane, gdy nie mamy wystarczającej ilości wektorów, mogących być bazowymi (rozwiązaniem dopuszczalnym jest rozwiązanie, którym nie wstępują niezerowe zmienne sztuczne)

30. Przyczyny i konsekwencje wprowadzania zmiennych osłabiających i zmiennych sztucznej bazy do warunków ograniczających zadania programowania liniowego

• osłabiające: wprowadzane, gdy warunki ogr. są wyrażone w postaci nierówności

• sztuczna baza: wprowadzane. Gdy po uzyskaniu postaci standardowej nie mamy podmacierzy jednostkowej m-tego stopnia

• konsekwencje: modyfikacja f-ji celu tylko w przypadku zmiennych sztucznej bazy

31. Idea algorytmu simplex

• metoda simpleks po znalezieniu początkowego rozwiązania bazowego dopuszczalnego wyznacza następne (sąsiednie) dopuszczalne rozwiązania bazowe zależne od poprzedniego, polepszające wartość funkcji celu. Przez sąsiednie rozwiązanie bazowe przyjmuje się rozwiązanie różniące się od niego tylko jedną zmienną bazową. (przeskakiwanie do sąsiedniego wierzchołka zbioru)

32. Wyznaczanie początkowego rozwiązania bazowego dopuszczalnego zadania programowania liniowego

• sprowadzenie zadania do postaci standardowej

• wyodrębnienie lub stworzenie podmacierzy jednostkowej (wprowadzenie wektorów sztucznej bazy)

33. Interpretacja elementów wektora wskaźników optymalności w tablicy simpleksowej

• wskaźniki optymalności informują nas:

1. czy dane rozwiązanie jest rozwiązaniem optymalnym

2. czy wprowadzenie danej zmiennej do bazy zwiększy czy zmniejszy wartość f-cji celu

34. Wyznaczanie elementu centralnego w tablicy simpleksowej

• obliczenie wskaźników optymalności

• sprawdzenie, czy dane rozwiązanie nie jest rozwiązaniem optymalnym

• wybranie wskaźnika optymalności o najwyższej wartości. Element centralny znajduje się w kolumnie nad tym wskaźnikiem. Sprawdzenie, czy nie mamy do czynienia z funkcją celu o nieograniczonej wartości

• kontrola, czy wszystkie elementy w wybranej kolumnie nie są <=0

• obliczenie ilorazu elementów x_b / x, wybór najmniejszego dodatniego ilorazu. EC znajduje się w tym wierszu

35. Kiedy aktualne dopuszczalne rozwiązanie bazowe zadania programowania linowego jest rozwiązaniem optymalnym (opisz etap algorytmu simpleks)

• wtedy, kiedy wskaźniki optymalności są <=0

36. Kiedy zadanie programowania liniowego nie ma skończonego rozwiązania optymalnego (opisz etap algorytmu simpleks)

• jeżeli istnieje j takie, że z_j-c_j>0 przy którym a_ij<=0 dla wszystkich i należące do B to zadanie nie ma skończonego rozwiązania optymalnego

37. Zadanie pierwotne, a zadanie poszerzone w metodzie simpleks

• funkcję celu modyfikujemy o współczynniki M przy dodatkowych wektorach sztucznej bazy

• modyfikujemy ograniczenia o wektory sztucznej bazy i osłabiające

• dodajemy kolejny wiersz w tabeli simpleksowej, obrazujący ilość współczynników M w danej kolumnie K

38. Wyznaczanie rozwiązania optymalnego zadania pierwotnego na podstawie rozwiązania optymalnego zadania poszerzonego

• gdy wśród zmiennych bazowych do rozwiązania optymalnego występują niezerowe zmienne sztuczne - zadanie wyjściowe jest sprzeczne

• gdy wśród zmiennych bazowych do rozwiązania optymalnego występując zerowe zmienne sztuczne - odrzucamy je i otrzymujemy rozwiązanie pierwotne

• gdy wśród zmiennych losowych nie ma zmiennych sztucznych - mamy rozwiązanie optymalne zadania wyjściowego

39. Postępowanie w przypadku degeneracji rozwiązania zadania programowania liniowego - metoda perturbacji

• występuje niezwykle rzadko w rzeczywistości

• degeneracja może prowadzić do cykliczności

• Jeśli zachodzi alternatywa wyboru nr-u wiersza zmiennej do usunięcia, to obliczamy ilorazy dla pozostałych wierszy, poczynając od 1 szukamy ilorazów x_i/x_k o najmniejszej nieujemnej wartości. Jeśli znaleźliśmy, to tę zmienną usuwamy z bazy, jeśli nie, to liczymy tak aż do końca tablicy sympleksowej i załamujemy się, bo wtedy nie wiemy, którą zmienną wprowadzić do bazy.

• Istnieje jeszcze kilka innych metod postępowania w przypadku degeneracji

40. Symetryczne / niesymetryczne pierwotne / dualne zadania programowania liniowego

• niesymetryczne zadanie dualne

• zadanie pierwotne: min f(x)=c^T X, AX=b, X>=0

• zadanie dualne: max g(w)=b^T X, A^T W <=c, brak wymagań, aby w_i>=0

symetryczne zadanie dualne

• zadanie pierwotne: min f(x)=c^T X, AX>=b. X>=0

• zadanie dualne: max g(w)=b^T X, A^T W<=c, W>=0

41. Postać ogólna zagadnienia transportowego

Niech x_ij (i=1..m, j=1..n) oznacza wielkość przewozu od i-tego dostawcy do j-tego odbiorcy

Sformułowane zadanie można zapisać w następującej postaci:

Postać funkcji celu

Warunki ograniczające:

(warunki bilansowe dostawców): „suma od j=1..n” xij<=ai, i=1..m

(warunki bilansowe odbiorców) „suma od i=1 do m” xij=bj j=1..n

xij>=0, i=1..m, j=1.n

gdzie:

X - macierz zmiennych decyzyjnych

z - wartość f-ji celu

C - macierz kosztów

a - wektor dostawy

b - wektor odbioru

42. Interpretacja warunków ograniczających zagadnienia transportowego

1. suma towarów wysyłanych do odbiorców musi być <= zasobom, które posiadają

2. suma towarów przyjmowanych przez odbiorców musi być równa zapotrzebowaniu odbiorców

43. Zadanie transportowe zbilansowane, niezbilansowane.

Zadanie zbilansowane:

tj. suma zasobów towarów jest równa sumie zapotrzebowań

Zadanie niezbilansowane - sumy te nie są sobie równe

44. Metody sprowadzania zadania transportowego do postaci zbilansowanej

• wprowadzenie fikcyjnego odbiorcy lub fikcyjnego dostawcy:

• fikcyjny odbiorca ma zapotrzebowanie
  

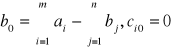
• fikcyjny dostawca ma zapas
  

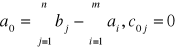
45. Czy zadanie transportowe zawsze posiada rozwiązanie optymalne?

Tak, jeśli jest to zadanie zbilansowane, a do takiej postaci możemy zawsze doprowadzić.

46. Czy zadanie transportowe zawsze posiada skończone rozwiązanie optymalne?

Jw - tak, jeśli jest to zadanie zbilansowane, a do takiej postaci możemy zawsze doprowadzić.

47. Warunki otrzymania rozwiązania zadania transportowego o wartościach całkowitych

Jeśli wszystkie a_i i b_j w zadaniu transportowym zbilansowanym są liczbami całkowitymi, to każde rozwiązanie bazowe (także optymalne) jest utworzone z liczb całkowitych

48. Liczba wszystkich zmiennych decyzyjnych w zadaniu transportowym o m dostawcach i n odbiorcach

m*n

49. Liczba zmiennych bazowych w rozwiązaniu bazowym zadania transportowego

Z ogólnych własności zadania programowania liniowego wynika, że rozwiązanie bazowe zadania transportowego składa się dokładnie z m+n-1 zmiennych bazowych.

50. Etapy procedury rozwiązywania zadania transportowego

• wyznaczanie wstępnego rozwiązania bazowego (np. metodą kąta północno-zachodniego, metodą minimalnego elementu macierzy kosztów, metodą VAM)

• wyznaczanie rozwiązania optymalnego (np. metodą potencjałów)

51.   Metody wyznaczania wstępnego rozwiązania bazowego zadania transportowego.

- metoda kąta północno-zachodniego

Wybieramy za każdym razem zmienną bazową, stojącą w rogu północno-zachodnim redukowanej macierzy przewozów X. Pierwszą zmienną bazową będzie zmienna x₁₁, ostatnią zmienna x_mn

- metoda minimalnego elementu macierzy kosztów

Jako pierwszą zmienną bazową wybieramy zmienną, której odpowiada najmniejszy współczynnik kosztu jednostkowego. Redukujemy zbiór dostawców lub zbiór odbiorców oraz korygujemy zasoby dostawców i zapotrzebowania odbiorców. Po redukcji ponownie wybieramy zmienną, której odpowiada najmniejszy współczynnik kosztu jednostkowego.

- metoda VAM

52.   Postępowanie w przypadku degeneracji rozwiązania bazowego zadania transportowego.

Jeżeli rozwiązanie zadania transportowego ma mniej niż M+n-1 zmiennych bazowych (tzw. zdegenerowane rozwiązanie bazowe, w którym co najmniej jedna zmienna bazowa jest równa zeru), należy dołączyć brakującą liczbę zmiennych bazowych z wartościami zerowymi. Wyboru dokonujemy tak, aby graf rozwiązania był grafem spójnym i bez cykli.

53.   Interpretacja elementów tablicy wskaźników optymalności w metodzie potencjałów.

Sprawdzamy, czy macierz wskaźników optymalności C⁰ >=0. Jeśli tak, rozwiązanie jest optymalne.

54.   Kryterium stopu w algorytmie rozwiązywania zadania transportowego metodą potencjałów.

Metoda z wykładu: wszystkie wskaźniki optymalności są liczbami dodatnimi

Metoda z ćwiczeń: wszystkie wskaźniki optymalności są elementami ujemnymi (jak w metodzie simpleks)

55.   Przykłady problemów decyzyjnych formułowanych w postaci zadania transportowego.

• zagadnienie transportowo-produkcyjne

• zagadnienie wyboru lokalizacji produkcji

• zagadnienie minimalizacji pustych przebiegów

---