Imię i nazwisko: Łukasz Chłopczyński
Wydział : Biotechnologii i nauk o żywności
Kierunek : Biotechnologia
Grupa : IV
Ćwiczenie nr 36
Tytuł ćwiczenia: Oznaczanie współczynnika podziału acetonu pomiędzy toluen i wodę metodą refraktometryczną.
Data wykonania ćwiczenia....................
Data oddania sprawozdania..................
Data zwrotu sprawozdania....................
Data ponownego oddania sprawozdania..............
Wstęp teoretyczny:
Rozpatrzmy ciekły układ trójskładnikowy, złożony z dwóch składników ciekłych, α i β, o ograniczonej rozpuszczalności wzajemnej oraz trzeciego składnika A, którym może być ciało stałe, ciecz lub gaz, który dobrze rozpuszcza się w obu cieczach. W stałej temperaturze i pod stałym ciśnieniem, ustala się równowaga dwóch faz ciekłych, którymi są roztwory składnika A w ciekłej fazie α i ciekłej fazieβ. Warunkiem równowagi jest równość potencjałów chemicznych każdego składnika w obu fazach. Dla składnika A można napisać następującą równość:
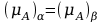
w której (μA)α oraz (μA)β oznaczają potencjały chemiczne tego składnika w każdej z faz. Uzależniając potencjał chemiczny składnika od jego aktywności termodynamicznej można napisać równanie:
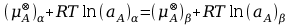
które można przekształcić do zależności:
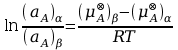
(aA)α i (aA)β oznaczają aktywność termodynamiczną składnika A w fazach α oraz β. (μA⊗)α oraz (μA⊗)β oznaczają standardowe potencjały chemiczne składnika A odpowiednio w fazach α oraz β. W stałej temperaturze i pod stałym ciśnieniem wyrażenie po prawej stronie powyższego równania jest wielkością stałą, co pozwala przekształcić to równanie do następującej postaci:
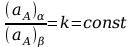
Jeżeli stężenia składnika A w obu są niewielkie można przyjąć, iż współczynniki aktywności termodynamicznej składnika A w obu fazach, (γA)α oraz (γA)β są bliskie jedności, co pozwala zastąpić aktywności termodynamiczne składnika (aA)α i (aA)β, ułamkami molowymi tego składnika, odpowiednio (xA)α i (xA)β:
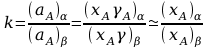
W roztworze rozcieńczonym liczba moli składnika A jest znacznie mniejsza od liczby moli rozpuszczalnika:
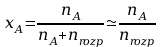
natomiast objętość roztworu rozcieńczonego jest praktycznie równa objętości rozpuszczalnika, co pozwala napisać następującą zależność określającą stężenie molowe składnika w roztworze:
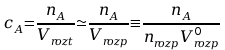
Uwzględniając powyższe zależności otrzymujemy równanie:
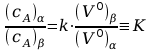
z którego wynika, że w dostatecznie rozcieńczonych roztworach stosunek stężeń składnika w dwóch współistniejących fazach ciekłych, zwany współczynnikiem podziału, jest stały i niezależny od stężenia.
Równanie Clausiusa – Clapeyrona:
Jeżeli
układ zawiera jeden składnik nie reagujący chemicznie
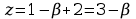 ,
więc w stanie równowagi mogą być 2 lub 3 fazy. Gdy mamy układ
dwufazowy ułamek molowy składnika „i” w każdej fazie jest
stały i jest wielkością niezmienną. Stan układu określa więc
ciśnienie p i temp T. Ponieważ
,
więc w stanie równowagi mogą być 2 lub 3 fazy. Gdy mamy układ
dwufazowy ułamek molowy składnika „i” w każdej fazie jest
stały i jest wielkością niezmienną. Stan układu określa więc
ciśnienie p i temp T. Ponieważ
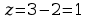 zatem jeden z 2 parametrów p lub T można dobrać dobrowolnie, a
drugi przybierze wartość zależną od pierwszego wynikającą z
praw równowagi termodynamicznej. Oznacza to, że obie wartości (p i
T) są od siebie zależne.
zatem jeden z 2 parametrów p lub T można dobrać dobrowolnie, a
drugi przybierze wartość zależną od pierwszego wynikającą z
praw równowagi termodynamicznej. Oznacza to, że obie wartości (p i
T) są od siebie zależne.
f(p,T) = 0 ; matematycznym wyrazem tej funkcji jest równanie C-C.
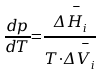
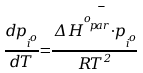
Gdzie
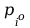 -
ciśnienie pary nasyconej przy czym
-
ciśnienie pary nasyconej przy czym
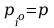 .
Gdy
.
Gdy
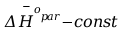
Po rozdzieleniu zmiennych i scałkowaniu :
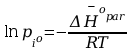 jak
widać
jak
widać
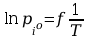
Gdzie
współczynnik kierunkowy -
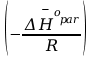
Wyszukiwarka
Podobne podstrony:
Ekonomia konspekt1
BLS 2010 stom [konspekt]ppt
Ekonomia konspekt6
22 Choroby wlosow KONSPEKTid 29485 ppt
konspekt dzieci , ćwicz
farmakoterapia w als, konspekt+RKO2011 farmakoterapia+[CPR+EU]
Ekonomia konspekt9
RKO farmakoterapia [konspekt
Ekonomia konspekt14
metodologia badan politologicznych konspekt
Konspekt; odejmowanie liczb wymiernych
0 konspekt wykladu PETid 1826 Nieznany
Konspekt projektu I część 2013
konspekt2
Historia stosunków miedzynarodowych konspekt wiedzy
AKTYWA PIENIĘŻNE KONSPEKT RF
2 konspekt lekcji 3cid 19552 Nieznany