EKONOMIA MATEMATYCZNA - ĆWICZENIA
Ćwiczenia z dnia 23.03.2014 r.
Zad. 1
Funkcję kosztów całkowitych opisuje równanie:
tc(y) = 3y2 + 100
Wyznaczyć funkcję:
kosztów zmiennych
przeciętnych kosztów stałych
przeciętnych kosztów zmiennych
przeciętnych kosztów całkowitych
kosztów krańcowych
Policzyć:
koszty zmienne,
koszty całkowite,
przeciętne koszty stałe,
przeciętne koszty zmienne,
przeciętne koszty całkowite,
koszty krańcowe.
Przy wielkości produkcji równej 200.
Przy jakiej wielkości produkcji przeciętne koszty całkowite są niższe od 9 ?
Przy jakiej wielkości produkcji przeciętne koszty całkowite są najmniejsze ?
Ad. 1

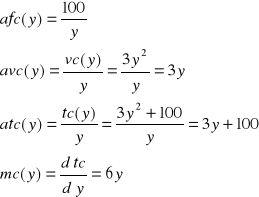
Ad. 2
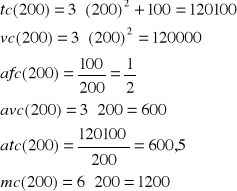
Ad. 3
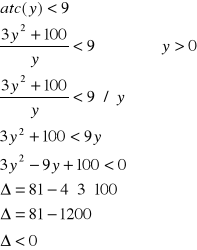
0 y
![]()
Ad. 4
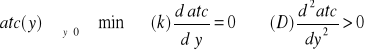
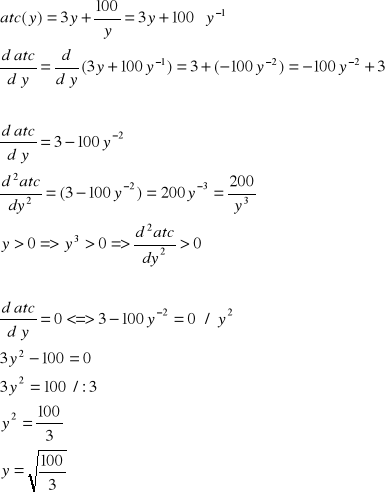
Przedsiębiorstwo ponosi najniższe przeciętne koszty całkowite przy produkcji równej ![]()
.
Zad. 2
![]()
Przy jakich wielkościach produkcji przeciętne koszty całkowite spadają poniżej 7 ?
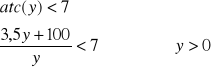
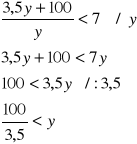
Jeżeli produkcja będzie większa od ![]()
to przeciętne koszty całkowite spadną poniżej 7.
Zad. 3
Funkcja kosztów całkowitych dana jest wzorem:
![]()
Przedsiębiorstwo działa w konkurencji doskonałej, cena produktu = 70.
Wyznaczyć : funkcję utargu i zysku przedsiębiorstwa
Zdefiniować pojęcie podaży
Wyznaczyć podaż
Policzyć: koszt całkowity, utarg i zysk odpowiadający podaży.
Ad.1
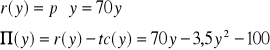
Ad. 2,3
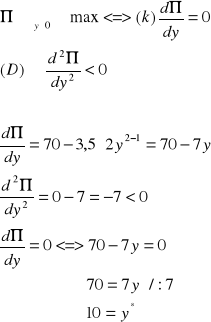
Przy produkcji równej 10, producent maksymalizuje swój zysk.
Ad.4
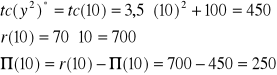
Wyszukiwarka
Podobne podstrony:
EKONOMIA MATEMATYCZNA 23.03.2014, IV rok, Wykłady, Ekonomia matematyczna
EKONOMIA MATEMATYCZNA 09.03.2014, IV rok, Ćwiczenia, Ekonomia matematyczna
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 22.03.2014, IV rok, Ćwiczenia, Ekonometria i prog
EKONOMIA MATEMATYCZNA 09.03.2014, IV rok, Wykłady, Ekonomia matematyczna
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 05.04.2014, IV rok, Ćwiczenia, Ekonometria i prog
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 27.04.2014, IV rok, Ćwiczenia, Ekonometria i prog
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 22.03.2014, IV rok, Wykłady, Ekonometria i progno
EKONOMIA MENADŻERSKA 07.03.2014, IV rok, Wykłady, Ekonomia menadżerska
EKONOMIA MENADŻERSKA 08.03.2014, IV rok, Wykłady, Ekonomia menadżerska
MAKROEKONOMIA ZAAWANSOWANA 08.03.2014, IV rok, Wykłady, Makroekonomia zaawansowana
EKONOMETRIA I PROGNOZOWANIE PROCESÓW EKONOMICZNYCH 17.05.2014, IV rok, Wykłady, Ekonometria i progno
EKONOMETRIA 25.03.2012, II rok, Ćwiczenia, Ekonometria
prawo o.s.23.03, administracja, II ROK, III Semestr, rok II, sem IV, prawo o.s
EKONOMETRIA 11.03.2012, II rok, Ćwiczenia, Ekonometria
EKONOMIA MENADŻERSKA 04.04.2014, IV rok, Wykłady, Ekonomia menadżerska
Interna 26.03.2014, weterynaria, 4 rok, notatki 2014
WNIOSKOWANIE STATYSTYCZNE 12.10.2013, IV rok, Ćwiczenia, Wnioskowanie statystyczne
WNIOSKOWANIE STATYSTYCZNE 26.10.2013, IV rok, Ćwiczenia, Wnioskowanie statystyczne
więcej podobnych podstron