10. Obciążenia układów kolejowego napędu trakcyjnego.

10.1. Ogólny podział obciążeń w układach transmisji momentu.

Ogólny podział (najogólniej rozumianych) obciążeń, zgodnie z terminologią powszechnie stosowaną w teorii ruchu pojazdów a także w teorii drgań i w dynamice maszyn, dotyczy charakteru tych obciążeń oraz wymuszeń (proces ustalony; drganiowy proces losowy; drganiowy proces zdeterminowany) oraz sposobu wzbudzenia drgań. Na schemacie poniżej podano terminologiczne zasady rozróżniania obciążeń panujących w układach napędowych. Ich ilustrację podano wcześniej na rysunku 3.8.

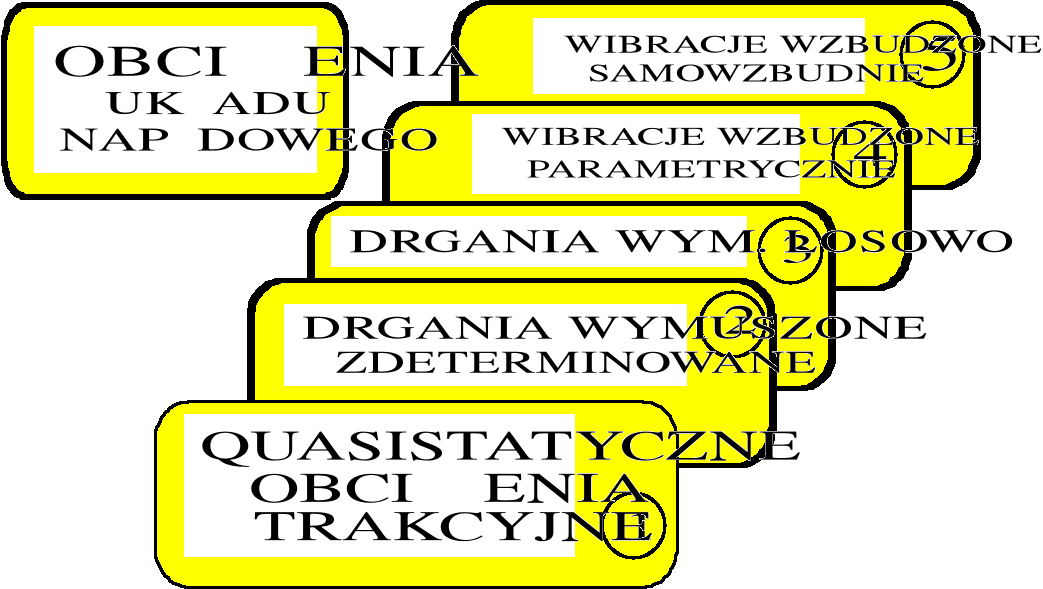
W tej części książki, mówiąc o modelowaniu dynamiki pominiemy zagadnienie Nr.1, fundamentalne z punktu widzenia wytrzymałości doraźnej elementów napędu: obciążenia quasistatyczne (trakcyjne). Pozostałe rodzaje obciążeń mają charakter wibracyjny i te zostaną, w kolejnych podrozdziałach, syntetycznie uwzględnione.

Największy zakres jakościowy ingerencji konstruktora w doskonaleniu układu występuje w odniesieniu do wymuszeń "twardych" zdeterminowanych (2) oraz eliminacji "miękkich" wzbudzeń parametrycznych (4) a także strukturalnie immanentnych dla napędu adhezyjnego samowzbudzeń (5): "twardych" przy poślizgach przerywanych ("stick - slip") oraz "miękkich" przy poślizgu rozwiniętym. W tym zakresie potrzebna jest wiedza dość wyspecjalizowana, wykraczająca poza ramy tematu niniejszej książki. Zainteresowany Czytelnik znajdzie podstawy tych zagadnień w pracach [1], [2], [3], [4].

Źródła zaburzeń dynamicznych w części mechanicznej układu napędowego ogólnie są pochodzenia "elektrycznego" (E) i "mechanicznego" (G). W odniesieniu do struktury własnej układu napędowego możemy wyróżnić zaburzenia "zewnętrzne" (od toru) jak też "wewnętrzne" (od przekładni G). Tę różnorodność w ich wzajemnym sprzężeniu ilustruje tabela 10.1.

Tabela 10.1

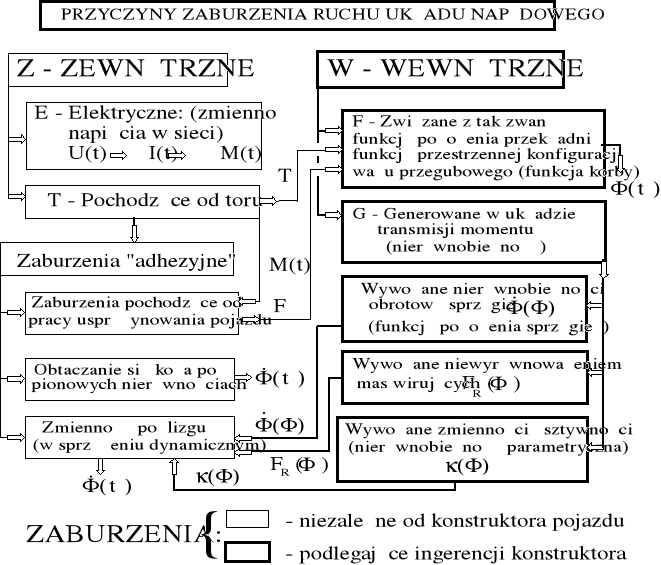
Tabela 10.1. Podział zaburzeń względem pochodzenia. Strzałkami wskazano wzajemne sprzężenia pomiędzy przyczynami zaburzeń traktowanymi umownie w sposób rozdzielny; dynamiczne poślizgi kół po szynach (nawierzchni), jakkolwiek wywołane przyczynami zewnętrznymi, mają związek z budową zespołu napędowego i zawieszenia pojazdu.

Źródłami wewnętrznymi wymuszeń drgań w układach napędowych są:

1. Niewyrównoważenia elementów wirujących;

2. Ogólnie niezerowe funkcje położenia sprzęgieł transmisji momentu napędowego;

3. Tętno pochodzące od (kineto)-statyki sprzęgieł wychylnych;

4. Niejednorodność charakterystyk sztywności i tłumienia obwodowo rozmieszczonych elementów podatnych w członach (tarczach) wirujących;

10.1.1. Niewyrównoważenie elementów wirujących.

Powszechnie znane zagadnienie wyrównoważania statycznego i dynamicznego elementów wirujących ma charakter ogólnotechniczny i w odniesieniu do mechanizmów napędowych pojazdów szynowych ma pełne zastosowanie. Zagadnienie to należy więc traktować jako rutynowe. Ma ono obszerną literaturę podręcznikową i poradnikową. Niewyrównoważenie rozumiane w sensie ogólnomaszynowym zostanie więc w tym miejscu pominięte.

Wyspecjalizowany zakres zagadnień związanych z niewyrównoważeniem wirujących mechanizmów sprzęgieł odsuwnych wchodzących w skład zespołu napędowego musi jednak znaleźć należyte potraktowanie. Rzecz dotyczy zwłaszcza układów napędowych Nr.4 oraz Nr.6, omówionych w tabeli 9.1 i oznaczonych jako IEUsNpS IEUsUpS. Zostały one pokazane na rysunkach 9.4 i 9.6.

Jest rzeczą charakterystyczną, że niemal wszystkie wirujące sprzęgła odsuwne [2] stanowiące, w sensie klasycznej teorii mechanizmów [1], mechanizm rzędu trzeciego [1], [2], wyróżniają się tym, że wektor niewyrównoważenia, przyporządkowany do "punktu charakterystycznego" (środka masy jarzma), wiruje (w zgodnym kierunku lecz) z podwojoną prędkością podstawową wału wirującego ("prędkość podstawowa" jest tu ściśle rozumiana w sensie wartości średniej - matematycznego momentu rzędu pierwszego). Sprzęgłom odsuwnym rzędu III poświęcono w niniejszej książce podrozdział 8.3.1. Trzy przykłady sprzęgieł odsuwnych rzędu III przedstawiono tam w tabeli 8.3.

Na rysunkach w tabeli 8.3, zaczerpniętych z pracy [2], pokazano postać trajektorii punktu charakterystycznego dla sprzęgieł odsuwnych według patentów Alsthom oraz Siemens.

Wartość modułu wektora niewyrównoważenia F = m2 zależy liniowo od wartości niewspółosiowości "e" połączonych poprzez sprzęgło wałów: napędzającego i napędzanego; gdzie:

m - masa niewyrównoważona grupy kinematycznej mechanizmu [1] sprzęgła odsuwnego zredukowana do geometrycznego środka jarzma,

- promień kołowej trajektorii punktu charakterystycznego,

- podstawowa prędkość kątowa wału napędzającego.

Zagadnieniu strukturalnego nie-wyrównoważenia elementów składowych układu napędowego ze sprzęgłami Alsthom poświęcono uwagę w pracy [5] przytoczonej w niniejszej książce w p. 8.3.4. Zagadnienie to dotyczy oddziaływań poprzecznych w stosunku do osi obrotu. Jakkolwiek proces niewyrównoważenia sprzęgieł Alsthom jest, pod względem częstości, zdeterminowany, to wartość sił niewyrównoważenia zależy od losowej wartości niewspółosiowości wału drążonego w stosunku do osi zestawu kół (rysunek 9.6).

Charakter tych wymuszeń jest więc mieszany: zdeterminowany z "szumem" losowym. W niniejszej książce nie ma miejsca na dalsze rozwijanie tego tematu. Jednakże modelowanie konturu dynamicznego ze sprzęgłami Alsthom, ze względu na drgania skrętne, stanowi treść p. 11.1.

10.1.2. Funkcje kątowego położenia sprzęgieł kompensujących niewspółosiowość łączonych wałów.

Funkcje położenia sprzęgieł odsuwnych opisują wartość kinematycznego zaburzenia kąta położenia wału napędzanego B w stosunku do wału napędzającego A, zależną od parametru niewspólosiowości "e", w funkcji zmiennej niezależnej jaką jest kąt obrotu wału napędzającego A; =t;

=+; =A; =B;

Funkcje położenia dwóch najczęściej w kolejnictwie stosowanych sprzęgieł odsuwnych przedstawiono w tabeli 8.3, wraz z odpowiednimi, zamieszczonymi tam wzorami; w pracy [2] jest tych sprzęgieł osiemnaście.

Funkcje położenia sprzęgieł wychylnych opisują wartość kinematycznego zaburzenia * kąta położenia wału napędzanego B w stosunku do wału napędzającego A, zależną od parametru (losowej!) niewspółosiowości wychylnej "", w funkcji zmiennej niezależnej - według opisu jak wyżej.

Postacie funkcji położenia sprzęgieł pracujących w warunkach ustalonych stanowią matematyczny opis zdeterminowanych zaburzeń ruchu.

10.1.3. Tętno, związane ze statyką sprzęgieł wychylnych, wywołujące zginanie wałów.

Ogólnie nierównobieżne sprzęgła wychylne (p. p. 8.5. i 8.6), w sposób immanentny, wywołują tętno obciążeń poprzecznych (w płaszczyźnie poprzecznej do osi wału), które stanowią zarówno wymuszenie drgań giętnych środkowego odcinka wału przegubowego jak też mogą stanowić wzbudzenie drgań wymuszonych oraz także parametrycznych kątowej przekładni osiowej (p.10.1). Drgania parametryczne zostały w skromnym zakresie omówione w p. 10.1. Obciążenia zginające i skręcające wału przegubowego zostały omówione w p. 8.7.

W tym miejscu zamieszczone zostaną jedynie elementarne uwagi odnośnie częstości wymuszeń, pochodzących od wału przegubowego, działających na kątową przekładnię osiową, przy zastosowaniu sprzęgieł krzyżakowych. Określają one podstawową charakterystykę tętna drgań wymuszonych, które w przypadku rezonansu, mogą zniszczyć układ napędowy. Rzecz dotyczy drgań obrotowych korpusu przekładni osiowej (rys. 9.7) wokół osi zestawu. Częstość własna tych drgań zależy od doboru sztywności ramienia reakcyjnego.

Moment My poprzeczny do osi wałka wejściowego (atakującego) przekładni osiowej, obciążonego momentem roboczym Mx wału przegubowego, wyraża się wzorem:

(10.1)

gdzie: - kąt załamania osi wału w sprzęgle;

- kąt obrotu wału wejściowego; = t;

- prędkość kątowa wału wejściowego (przegubowego) [1/s].

Częstość wymuszeń drgań obrotowych przekładni osiowej wynosi więc:

(10.2)

gdzie: V - prędkość jazdy [m/s];

Dk - średnica okręgu koła jezdnego [m];

i1, i2 - wartości przełożeń poszczególnych stopni przekładni.

Częstość własna obrotowych drgań przekładni osiowej wokół osi zestawu zależy od wartości dynamicznych jej elementów (masy i masowe momenty bezwładności) oraz od parametrów ramienia i cięgła (drąga) reakcyjnego.

10.1.4. Niejednorodność charakterystyk sztywności i tłumienia obwodowo rozmieszczonych elementów podatnych.

Niejednorodność charakterystyk obwodowo rozmieszczonych elementów podatnych stanowi źródło wzbudzenia drgań parametrycznych w układzie napędowym. Odpowiednie wzory stanowiące opis niejednorodności charakterystyk podano książce [6]. W książce [2] natomiast podano przykład matematycznego modelowania układu napędowego Nr. 2 IETUz pokazanego schematycznie na rysunku 9.2.

Drgania parametryczne są właściwe tylko niektórym strukturom mechanicznym napędu trakcyjnego. Szczególnie unikalną odmianą drgań parametrycznych charakteryzuje się układ napędu ze sprzęgłem Alsthom, którego część masy zredukowanej jest synchronicznie przepompowywana z wału drążonego na oś zestwu i odwrotnie. Istota tego zjawiska została omówiona w p. 8.3.4.

10.1.5. Źródła zewnętrzne dynamicznych losowych zaburzeń ruchu i ich charakterystyki.

O źródłach dynamicznych zaburzeń ruchu była już mowa we wprowadzeniu do rozdziału 3. Tam też zostały omówione przede wszystkim wymuszenia zdeterminowane. W tym miejscu należy zamieścić uzupełniający komentarz odnośnie dynamicznych wymuszeń losowych.

W technice napędu trakcyjnego pojazdów szynowych najsilniejszy losowy wpływ dynamiczny na zaburzenia ruchu obrotowego elementów transmisji momentu napędowego wywierają:

a) - pionowe nierówności toru i drgania pionowe zestawu i szyn związane ze sprężystością toru,

b) - obtaczanie się kół po makronierównościach pionowych toru.

Ta pierwsza przyczyna zaburzeń ruchu nie ma bezpośredniego związku z procesem adhezyjnym.

Pionowe nierówności toru i drgania układu: koło - szyna, stanowią losowe wymuszenie sprzężone drgań obrotowych układu napędowego poprzez niezerowe funkcje położenia przekładni i sprzęgieł. Narastanie drgań obrotowych układu napędowego jest jednak silnie ograniczane od strony zestawu dzięki tłumiącemu działaniu sił przyczepności.

Druga przyczyna drgań w układzie napędowym ma dokładnie odwrotne działanie. Obtaczające się po pionowych makronierównościach toru koło, jest przyspieszane (adhezyjnie) na spadkach i wzniesieniach tych makronierówności, oraz jest adhezyjnie spowalniane jedynie na wierzchołkach i w zagłębieniach pofalowań. W rezultacie tych przeciwnych sobie zjawisk, zaburzenia osiągają poziom wynikający z równowagi dynamicznej. Sprzężony proces dynamiczno - tribologiczny, który może być lokalnie niestabilny, może stanowić przyczynę falistych zużyć szyn. Faliste zużycie szyn stanowi poważne, aktualne zagadnienie naukowe dotąd do końca nie rozwiązane.

Gdyby koło toczyło się bez poślizgów, to jego prędkość obrotowa wyniosłaby:

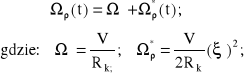
(10.3)

Wzór (10.3) wynika wprost z geometrii różniczkowej.

przy czym:

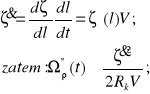
(10.4)

gdzie:
- współrzędna pionowego położenia środka koła w funkcji drogi "l".

W rzeczywistości mamy do czynienia z poślizgami koła po szynie wywołanymi zarówno skończoną (znaczną) wartością momentu bezwładności koła jak i z występowaniem momentu obrotowego napędowego. Zaburzenie prędkości obrotowej pochodzące od poślizgów koła na szynie prostej wynosi więc:

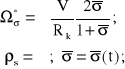
(10.5)

Znaki górne odpowiadają przyspieszaniu, dolne - hamowaniu.

Jest rzeczą charakterystyczną, że przy statycznym nacisku pojedynczego koła na tor Q=5104 [N] i współczynniku przyczepności =0,2, w ruchu koła kolejowego R=0,5 [m] po zdeterminowanej nierówności harmonicznej:

o amplitudzie a=50,5 [mm] i długości fali L=2 [m] z prędkością 30 [m/s], wszelka przyczepność byłaby dynamicznie wyczerpana; w tych warunkach całkowicie znika zdolność do wywiązywania jakiejkolwiek siły trakcyjnej. W obliczeniu przyjęto masowy moment bezwładności koła wynoszący 70 [kg m2].

Przy amplitudzie nierówności harmonicznej a=2 [mm], dynamiczne wyczerpanie przyczepności, opisanych warunkach, wynosiłoby zaledwie 1,56%.

Losowe wymuszenia dynamiczne [X(t)] pochodzące od toru opisywane są przez podstawowe charakterystyki probabilistyczne: funkcję gęstości prawdopodobieństwa p(X), wariancję x2, odchylenie standardowe x i wartość średniokwadratową XRMS.

Umiejętność wykorzystania podstawowych charakterystyk probabilistycznych w zadaniach badawczych i konstrukcyjnych należy do rutynowego warsztatu współczesnego inżyniera. Zagadnieniom tym poświęcono miejsce w pracy [2].

10.1.6. Literatura źródłowa:

[1] Artobolewskij I. I.: Mechanizmy v sovremennoj technikie. Moskwa "Nauka" 1970.

[2] Madej J.: Mechanika napędu pojazdów szynowych... PWN Warszawa 1983.

[3] Madej. J.: "Zjawiska dynamiczne w indywidualnym, symetrycznym układzie napędu lokomotywy przy naruszeniu przyczepności kół do toru" POJAZDY SZYNOWE 1/1976.

[4] Madej. J.: "Dynamika zaburzenia przyczepności zestawu kół pojazdu trakcyjnego przy niesymetrycznym przyłożeniu sił czynnych" POJAZDY SZYNOWE 2/1976.

[5] Madej. J.: Obraz oddziaływań w węzłach zespołu napędowego ze sprzęgłami typu Alsthom. Prace Naukowe Instytutu Konstrukcji i Eksploatacji Maszyn Politechniki Wrocławskiej. Nr. 48; 1986.

329

---