Rozdział 7

MECHANIZM RÓŻNICOWY O PROGRAMOWANYM TARCIU WEWNĘTRZNYM

Jak wspomniano w rozdziale 3, mechanizm różnicowy wbudowany do napędnej osi pojazdu niweczy kontur adhezyjny i odbiera osi rolę sterującą. W określonych warunkach trakcyjnych pewien zaprogramowany zakres współ-sterowalności pojazdu samochodowego przez oś napędną może się jednak okazać nad wyraz korzystny. Dotyczy to - na przykład - przypadków ruszania samochodu na oblodzonej jezdni, ciężkiej, stabilnej orki ciągnikiem kołowym z nienapędną osią przednią, lub sportowego pokonywania zakrętów z poślizgiem.

Dla poprawy warunków ruszania autobusów na oblodzonej, pod jednym kołem, jezdni problem rozwiązuje się współcześnie poprzez zastosowanie automatyki przeciwpoślizgowej, która sprawia "podhamowywanie" tego koła należącego do osi napędnej, które ma większą prędkość obrotową. W tym celu jednak układ hamulcowy każdego koła pojazdu musi być sterowany niezależnie. Pod względem trakcyjnym rozwiązanie takie wykazuje niedosyt racjonalności:

ponad dwukrotnie osłabia siłę pociągową wynikającą z momentu doprowadzonego do przekładni głównej a ponadto,

przyczepność koła zahamowanego (choćby szczątkowa), zamiast pomagać w napędzaniu pojazdu, wywiera nań wpływ hamujący.

Wbudowanie mechanizmu różnicowego o odpowiednio zaprogramowanym tarciu wewnętrznym do napędnej osi pojazdu może być traktowane jako rozwiązanie alternatywne do wyżej wspomnianego. Zaprogramowane tarcie wewnętrzne w mechanizmie różnicowym wprowadza do osi napędnej sterujący kontur adhezyjny pracujący jedynie w określonych warunkach obciążeń i samoczynnie wyłączający się po zmianie parametrów ruchu pojazdu.

W niniejszym rozdziale rozpatruje się podstawy teoretyczne i zasady projektowania nieczułości różnicowej czyli odpowiednich charakterystyk (progresywnych i degresywnych) zaprogramowanego tarcia wewnętrznego w mechanizmie różnicowym [10; 13].

7.1. Analog dźwigniowy - elementarne zjawiska fizyczne.

Mechanizm różnicowy, zarówno symetryczny jak i niesymetryczny, najprościej może być odwzorowany poprzez analog dźwigniowy. Odwzorowanie to jest metodycznie użyteczne w zrozumieniu kolejnych stopni złożoności układu niezbędnym dla racjonalnego zaprojektowania progresywnej charakterystyki mechanizmu. Rozważania będziemy prowadzić na przykładzie mechanizmu symetrycznego, który ma różnicowe przełożenie kinematyczne ik=1; (definicja poniżej). Analog dźwigniowy powszechnie znanego (najczęściej symetrycznego) mechanizmu różnicowego, przedstawiono poniżej, na rysunku 7.1.

RYSUNEK 7.1

Rysunek 7.1. Analog bloczkowy lub dźwigniowy powszechnie znanego, symetrycznego mechanizmu różnicowego. Na rysunku, dźwignia D symbolizuje satelitę wraz z kołem półosi mechanizmu. Moment MT w dźwigni traktowany jest jako wypadkowy moment tarcia występującego w obrębie kosza satelitów. Indeks "w" odnosi się do obciążenia wypadkowego.

Wywiązywanie różnych wartości sił FL FP, odpowiadających składowym obwodowym sił międzyzębnych, jest możliwe jedynie w warunkach występowania (analogowego) momentu tarcia MT pomiędzy dźwignią D i wieszakiem W:

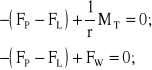
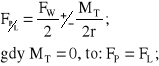
(7.1a)

albo we współrzędnych bezwymiarowych, jakie możemy wprowadzić po obustronnym podzieleniu (7.1a) przez FW/2, otrzymujemy:

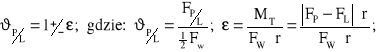
(7.1b)

Konsekwentnie wobec (7.1a) i (7.1b) oznaczymy w dalszym ciągu:

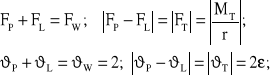
(7.1c)

W rozpatrywanym przypadku symetrycznym, przełożenie kinematyczne ik, według założenia, wynosi:

(7.2)

Tradycyjne pojęcie wewnętrznego przełożenia kinematycznego ik mechanizmu różnicowego jest bowiem związane z kierunkami względnych przemieszczeń ogólnych jego półosi xL i xP lub prędkości tych półosi

Charakterystykę
, zgodnie z (7.1c), przedstawiono na rysunku 7.2.

RYSUNEK 7.2.

Rysunek 7.2. Bezwymiarowo ujęta charakterystyka mechanizmu różnicowego z tarciem wewnętrznym o stałej wartości. Konsekwentnie, = const.

Wyrażone bezwymiarowo obciążenie nominalne mechanizmu jest traktowane jako suma obciążeń półosi. Wartość tego obciążenia stanowi parametr roboczy układu. Natomiast parametrem nieczułości różnicowej układu może być albo (bezwymiarowy) współczynnik stałego momentu tarcia wewnętrznego według (7.1b) albo też rozumiane jako stosunek momentu tarcia do momentu roboczego:

(7.1e)

Z rysunku 7.2 widzimy, że =const; Nawet w granicznym przypadku P,L=0, istnieje pewna ograniczona możliwość przenoszenia obciążenia P,L;
Jakkolwiek zbudowanie mechanizmu różnicowego z tarciem wewnętrznym o stałej wartości jest rzeczą bardzo łatwą, to wadą takiego układu jest niewrażliwość wartości momentu tarcia MT na wartość wypadkowego obciążenia roboczego FW. Z tej przyczyny poniżej rozważymy płaski analog mechanizmu różnicowego z tarciem proporcjonalnym do obciążenia roboczego.

Model układu z siłami tarcia proporcjonalnymi do obciążenia roboczego.

Omawiany model przedstawiono na rysunku 7.3.

RYSUNEK 7.3

Rysunek 7.3. Dźwigniowy, płaski analog mechanizmu różnicowego zapewniający proporcjonalność uogólnionych sił tarcia wewnętrznego do przenoszonego przezeń obciążenia roboczego.

Rysunek 7.3 ilustruje uproszczone rozkłady sił tarcia dla ogólnego, niesymetrycznego rozkładu obciążenia dźwigni bocznych. Przewidując techniczną adekwatność analogu dla mechanizmów strukturalnie symetrycznych, z kołami satelitarnymi w postaci walcowej o uzębieniu śrubowym, dalszą uwagę poświęcimy przede wszystkim takiemu przypadkowi. [Zapewnienie niesymetrii podziału obciążenia półosi w rzeczywistym mechanizmie różnicowym jest możliwe także w odmienny sposób niż w prezentowanym tutaj analogu dźwigniowym. Dla potrzeb dalszego studium zagadnień elementarnych, pozostaniemy jednak - na początek - przy tym analogu.].

Model układu realizuje siły tarcia tylko pomiędzy ślizgami wieszaka W a ślizgami dźwigni bocznych: lewej L i prawej P. Jest rzeczą oczywistą, że w przypadku, gdy kąt pochylenia ślizgów jest mniejszy od kąta tarcia =arc tg , to układ, pod obciążeniem roboczym FW, może ulegać zakleszczeniu i ruch jednej dźwigni bocznej może zachodzić tylko w przypadku ujemnego obciążenia drugiej dźwigni, koniecznego dla odkleszczenia systemu różnicowego. Na tej zasadzie pracują wszystkie różnicowe mechanizmy samohamowne, najczęściej ślimakowe.

Należy zauważyć, że w przypadku L=P=; przemieszczenia xP i xL są przeciwnie skierowane a ich wartości są jednakowe; przełożenie i = 1;

Obciążenia robocze FL i FP dźwigni bocznych powstają jako następstwo nakładania się dwóch zjawisk: statyki równowagi układu wyidealizowanego (bez tarcia) oraz quasistatyki ruchu układu rzeczywistego (z tarciem). Obydwa te zjawiska zostały odpowiednio zilustrowane rysunkami 7.4a i 7.4b.

RYSUNEK 7.4.

Rysunek 7.4. Ilustracja nakładania się dwóch zjawisk: statyki równowagi układu wyidealizowanego (bez tarcia) oraz quasistatyki ruchu układu rzeczywistego (z tarciem).

Zgodnie z ilustracją a), wartość pionowej składowej F siły Nw jest zależna od kąta :

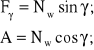
(7.2)

Ta sama siła Nw, zgodnie z ilustracją b), w inicjowanym ruchu wywołuje powstanie siły tarcia T:

(7.3)

Współczynnik tarcia , zgodnie z rysunkiem 4b, określa kąt tarcia
, przy czym:

(7.4)

Działająca na dźwignię przesuwną siła tarcia T ma zwrot przeciwnie skierowany do inicjowanego kierunku ruchu

(7.5)

Wypadkowa siła w dźwigni P wynosi: FP=F+FT; albo:

(7.6)

Zatem:

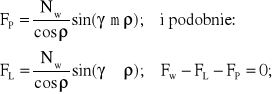
(7.7)

Gdzie: znak górny dotyczy zwrotu prędkości ruchu dźwigni P skierowanego ku górze; zaś dźwigni L - ku dołowi.

RYSUNEK 7.5.

Rysunek 7.5. Ilustracja stanów obciążeń FP1, FP2, FP3 układu niesamohamownego dla niżej wymienionych przypadków:

1 - przemieszczenie dźwigni P ku dołowi,

2 - bezruch dźwigni zarówno P jak i L,

3 - przemieszczanie dźwigni P ku górze.

Przypadek samohamowności zachodzi gdy ρ ≥ γ. W przypadku samohamownym (lub granicznym, gdy ρ  γ dowolnie duża siła Fw może być przenoszona tylko przez jedną z dźwigni: L lub P, wtedy jednak, ewentualne ujemne przemieszczenia x, (dźwigni obciążonej) w stosunku do wieszaka W, mogą być sterowane jedynie poprzez narzucenie dodatnich przemieszczeń na dźwignię nieobciążoną. Przemieszczeniom tak sterowanym, w układzie fizycznym musi towarzyszyć występowanie małej, ujemnej siły na tej nieobciążonej dźwigni. Zerowej wartości wypadkowej siły wieszaka Fw towarzyszy zerowa wartość siły Nw.

W przypadku
pracuje tylko dźwignia L. Jest to techniczny przypadek pracy mechanizmu różnicowego z przenoszeniem pełnego obciążenia przez koło wewnętrzne podczas ruchu pojazdu po łuku. Koło zewnętrzne steruje wartością poślizgu dx/dt tak, aby to pełne czynne obciążenie realizowało się przy prędkości średniej kół: wewnętrznego i zewnętrznego. Opisanemu zjawisku towarzyszy wywiązywanie się ciepła na powierzchniach ciernych. Zagadnieniu temu zostało poświęcone oddzielne miejsce w paragrafie 7.4 niniejszego rozdziału.

W omawianym przykładzie mechanizmu analogowego (przedstawionego na rysunku 7.3), mamy dwa techniczne przypadki obciążeniowe skojarzone ściśle z kierunkiem ruchu dźwigni:

- przypadek a) - dolne znaki w wyrażeniach (7.7); oraz

- przypadek b) - górne znaki w wyrażeniach (7.7);

(7.8)

Przy kontynuacji zapisu we współrzędnych bezwymiarowych według (7.1c) obowiązują następujące oznaczenia:

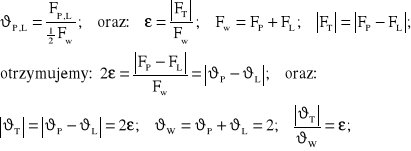
(7.9)

Dla przypadków a) i b) według (7.8), zgodnie z (7.1e) otrzymujemy:

(7.10)

Dla obydwóch przypadków a) i b), zachowuje więc moc także zależność odwrotna:

(7.11a)

Wielkość , zgodnie z interpretacją wyrażenia (7.9), możemy nazwać współczynnikiem obszaru różnicowej nieczułości mechanizmu czyli współczynnikiem udziału tarcia w stosunku do (bieżącego) obciążenia mechanizmu. W omawianym przypadku tarcie jest proporcjonalne do obciążenia roboczego wypadkowego =(FW).

Charakterystykę FL(FP), lub w ujęciu bezwymiarowym L(P, zgodnie z (, dla przypadku niesamohamownego, według rys.7.5, przedstawiono na rysunku 7.6a.

RYSUNEK 7.6A

Rysunek 7.6a. Charakterystyka mechanizmu niesamohamownego. Obszar zaprogramowanej (progresywnie narastającej wraz z obciążeniem) strefy nieczułości różnicowej zawiera się wewnątrz strefy ograniczonej polem zakreskowanym. Symbolika m jest opisana wzorami (7.8).

Przyjmując przykładowo =0,5, zgodnie z (11a), otrzymujemy m = 3. Przyjmijmy w dalszym ciągu, że wielkości m >1 we współrzędnych FL(FP) wykresu odpowiada przypadek a) czyli FP>FL. W takim przypadku, na mocy (7.8), zgodnie z rysunkiem 7.6a otrzymujemy:

Dla =0,5 otrzymamy:
Oczywiście,
Sens oznaczeń a, b, m, przyjętych powyżej, zilustrowano rysunkami 7.6a, 7.6b i 7.6c.

Pod względem ilościowym podział momentu w obszarach a) oraz b) (pokazanych na rysunku 7.6a) będziemy nazywać, według (7.11), współczynnikiem podziału momentu.

(7.11b)

W dalszym ciągu będziemy wykorzystywać symetrię wykresu względem prostej L  P, ograniczając rozważania wyłącznie do przypadku a) - części dolnej wykresu, według rysunków 7.6a i 7.6b, poniżej prostej m=1.

Zgodnie z powyższą umową, na mocy ( możemy napisać:

(7.12a)

Zauważmy, że po rozwinięciu prawej strony (7.12a) i uporządkowaniu, zgodnie z zapisem (7.11b), otrzymujemy wzór bardzo ważny dla konstruktorów:

(7.12b)

Wzór dotyczy modelu mechanizmu ze ślizgami płaskimi według rysunku 7.3.

RYSUNEK 7.6.B

Rysunek 7.6b. Ilustracja graficzna pomiędzy zależnościami występującymi we wzorach 7.8 - 7.11. Jako oznaczono współczynnik wykorzystania obciążenia nominalnego: =Fw/Fwnom.

Ze związków (7.12) widzimy, że współczynnik według (7.11b) - rys. 7.6a, w praktyce należy identyfikować ze stałą układu mechanicznego: [tg /tg ].

Związki (7.11) i (7.12) określają relację parametrów obszaru nieczułości , współczynnika podziału momentu m, współczynnika tarcia , (reprezentowanego przez kąt tarcia ρ, zgodnie z (7.4)) oraz geometrycznej wartości kąta pochylenia umownych ślizgów ciernych γ.

W podsumowaniu niniejszego punktu należy podkreślić, że charakterystyki mechanizmu różnicowego według rysunku 7.3, o programowanym tarciu wewnętrznym, podstawowo określają następujące parametry według (7.12a) i (7.12b) oraz (7.1b) i (7.1e):

(7.13)

RYSUNEK 7.6C.

Rysunek 7.6c. Ilustracja progresywnej charakterystyki T(W); albo FT(FW);

m - według (7.12a); - według (7.-12b);

Model układu z dodatkową składową sił tarcia

Schemat mechanicznego analogu układu mechanizmu różnicowego z dodatkową składową sił tarcia przedstawiono poniżej na rysunku 7.7. Każda dźwignia jest obciążona stałą - co do wartości i kierunku działania - siłą S, pochodzącą od wstępnie napiętej sprężyny.

Stała siła S, działająca na dźwignię (ku dołowi - rys. 7.7), zgodnie ze zwrotem sił FPS i FLS, jest równoważona dodatkową składową Fs (według rys. 7.4a), mającą zwrot dodatni skierowany ku górze.

Pozioma siła A, działająca na dźwignię prawą, dzięki pływającej opasce, równoważy się z poziomą siłą działającą, w kierunku przeciwnym, na dźwignię lewą.
Traktując siłę N jako znaną, na podstawie (7.7), możemy napisać wzory analogiczne do (7.7) przy czym skutek działania siły S jest ukryty w N i na razie pozostaje niejawny:

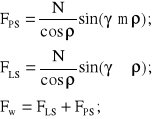
(7.14)

Gdzie: znak górny dotyczy zwrotu prędkości ruchu dźwigni P skierowanego ku górze, dźwigni L - ku dołowi. N - odpowiednio powiększona siła normalna. Dla przypadku a), FPS > FLS, będziemy w dalszym ciągu stosować znaki dolne.

Siła S stanowi wewnętrzne, dodatkowe obciążenie układu w konturze: wieszak - dźwignia - opaska - wieszak, wywołując zwiększoną, w stosunku do skutków obciązenia roboczego, siłę tarcia.

(7.15)

Gdzie Nw - obciążenie normalne na ślizgu pochodzące od obciążenia roboczego dźwigni według rysunku 7.5.

NS - obciążenie normalne pochodzące od siły S.

Wzorując się na zależności (7.2) otrzymujemy:

(7.16)

Zatem wypadkowa według (7.15) i (7.16) wartość siły normalnej N wynosi:

(7.17)

RYSUNEK 7.7.

Rysunek 7.7. System cierny dźwigni mechanizmu z napięciem wstępnym.

Dzięki występowaniu S>0, mamy N>Nw; przy czym Fw - taka sama siła wypadkowa według (7.7) jak w przypadku pokazanym na rysunku 7.3.

Teraz wyznaczymy wypadkową siłę tarcia FT według (7.14):

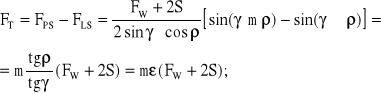
(7.18)

Zauważmy, że ograniczając zapis do przypadku gdy dźwignia "P" przemieszcza się ku dołowi (rys.7.7), we wzorze (7.18) pozostanie znak dolny:

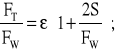
(7.19)

RYSUNEK 7.8.

Rysunek 7.8. Ilustracja graficzna charakterystyki FTS(FW) dla modelu mechanizmu z dodatkową stałą składową sił tarcia na tle przypadku FT(FW) bez składowej S.

Dolna powierzchnia na rysunku 7.8 w formie prostokąta, pokratkowana, odpowiada charakterystyce FL(FP) pokazanej na rysunku 7.2; górna powierzchnia, w formie trójkąta, zakreskowana ukośnie, odpowiada charakterystyce FL(FP) pokazanej na rysunkach 7.6a, 7.6b i 7.6c. Model układu z dodatkową składową sił tarcia jest więc modelem superpozycyjnym poprzednio analizowanych dwóch odmian modeli mechanizmu.

Wykorzystując związki (7.9) możemy napisać:

(7.20)

Współrzędne wykresu przedstawionego na rysunku 7.7 możemy wyrazić nieco inaczej wprowadzając (zilustrowany powyżej rysunkiem 7.6b) współczynnik wykorzystania obciązenia nominalnego :

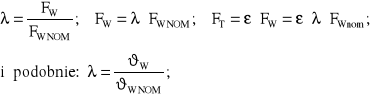
(7.21)

Dzięki wyrażeniom (7.21) istnieje łatwość wzajemnego kojarzenia charakterystyk mechanizmu w ujęciu FT(FW) z ujęciem FL(FP) lub podobnych charakterystyk bezwymiarowych.

Zgodnie z rysunkiem 7.8 oraz wzorem (7.19), stosunek 2S/Fw charakteryzuje udział siły wewnętrznej, panującej w sprężynie, w stosunku do bieżącej wartości roboczego obciążenia zewnętrznego.

RYSUNEK 7.9

Rysunek 7.9. Charakterystyka mechanizmu, przedstawionego na rysunku 7.7 z dodatkową siłą tarcia 2S w konturze wewnętrznym. Prosta =1 odpowiada obciążeniu znamionowemu. Wielkość opisuje strefę nieczułości bezwzględnej: we współrzędnych L(P), =2S/FWNOM; We współrzędnych FL(FP), =2S;

Stałe pole nieczułości różnicowej, pochodzące od siły 2S, oznaczono jako pokratkowane. Pole charakterystyk nieczułości progresywnej, zależnej od obciążenia roboczego mechanizmu, sprzężone z polem stałym poprzez wartość wybranego , zależy od kąta tarcia oraz kąta pochylenia ślizgów ,

132

---