CZĘŚĆ II: TRANSMISJA MOMENTU TRAKCYJNEGO

POMIĘDZY OSIAMI WZGLĘDEM SIEBIE NIERUCHOMYMI

Rozdział 5.

PRZEKŁADNIE OGÓLNIE HIPOIDALNE

5.1. Pojęcia podstawowe

Zwichrowane osie dwóch obracających się wałów, pomiędzy którymi należy przenosić moment napędowy, stanowią najogólniejszy, przestrzenny przypadek ich konfiguracji. Najprostszym, bezpośrednim sposobem transmisji momentu pomiędzy zwichrowanymi względem siebie osiami jest zastosowanie przekładni zębatej z kołami hiperboloidalnymi. Jedynym wymaganiem w tym przypadku jest stałość wartości parametrów zwichrowania: kąta oraz odległości pomiędzy zwichrowanymi osiami.

Pojęcie "koło hiperboloidalne" pochodzi od hiperboloidy obrotowej będącej przestrzenną, obrotową, prostokreślną figurą geometryczną, której powierzchnię tworzącą określają dwie rodziny linii prostych: lewozwojnych i prawozwojnych.

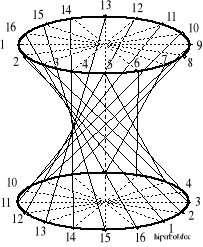
Rysunek 5.1. Hiperboloida jednopowłokowa. Figura ma dwie rodziny prostych tworzących powłokę: proste ułożone "lewozwojnie" i "prawozwojnie". Na rysunku pokazano jedynie tworzące proste ułożone lewozwojnie.

Tworzące powłokę proste mogą być nachylone pod dowolnym kątem "zwichrowania" w stosunku do osi figury. Dla dowolnych geometrycznych warunków wichrowatości osi dwóch wałów w przestrzeni można tak odpowiednio dobrać dwie hiperboloidy teoretyczne, współpracujące ze sobą w kinematycznym styku prostoliniowym wzdłuż ich tworzących, że zostanie także spełniony wymagany warunek wartości przełożenia przekładni. W praktyce jedynym ograniczeniem technicznym jest relatywnie niska sprawność przekładni w granicznych warunkach doboru jej parametrów. Zagadnieniu temu poświęcimy uwagę w dalszym ciągu niniejszego rozdziału.

W polskiej literaturze technicznej przekładnie z kołami hiperboloidalnymi noszą ogólną nazwę "przekładnie hipoidalne". W klasyfikacji [2] obok przekładni hipoidalnych wprowadzono także pojęcie "przekładnie spiroidalne".

Najogólniej rozumiane przekładnie hipoidalne stanowią rozwiązanie pośrednie pomiędzy przekładnią ślimakową a przekładnią stożkową. Przekładnia stożkowa stanowi prosty mechanizm kulisty, którego obydwa koła mają osie przecinające się, leżące we wspólnej płaszczyźnie. Przekładnia stożkowa stanowi szczególny graniczny przypadek przekładni hipoidalnej.

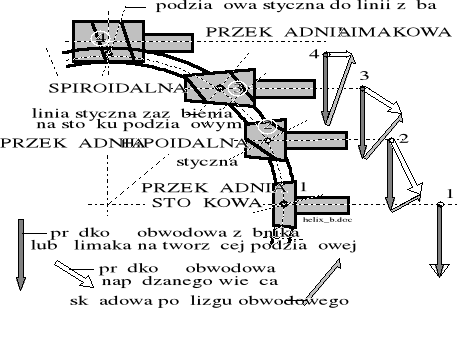
Rysunek 5.2. Klasyfikacja dwukołowych przekładni zębatych oraz odpowiednie rozkłady obwodowych i poosiowych prędkości poślizgu międzyzębnego przy jednakowej prędkości obwodowej zębnika napędzającego w średnim punkcie styku.

Konfiguracja przestrzenna dwóch hiperboloid w styku liniowym.

Ilustrację zestawienia dwóch hiperboloid w ogólnym przypadku przestrzennej konfiguracji ich osi pokazano na rysunku 5.3. Zgodnie z rysunkiem 5.3 przeniesienie ruchu obrotowego z wału aktywnego A na wał bierny B, zależnie od kierunku zwojności prostych, może być zrealizowane w dowolnym kierunku: w lewo lub w prawo. (Nie możemy tu ściśle mówić o kierunku "linii śrubowej", gdyż zęby teoretyczne na hiperboloidzie są odcinkami linii prostej a nie śrubowej). Obydwa koła mają zawsze ten sam, wybrany kierunek zwojności zębów. Z punktu widzenia kinematyki transmisji momentu nie ma znaczenia czy są to (przybliżone) koła śrubowo - walcowe, czy (przybliżone) koła stożkowe. Kształt koła zależy od pozostającej do wypełnienia odległości pomiędzy osiami, od wartości obciążeń roboczych i oczekiwanych sprawności przekładni przy pracy w każdym z obydwóch możliwych kierunków ruchu. Ogólnie bowiem sprawność ta może być zaprojektowana niesymetrycznie. Kierunek zwojności linii zębów na współpracujących ze sobą hiperboloidach teoretycznych jest zawsze taki sam: lewy - lewy, lub prawy - prawy.

W przekładni hipoidalnej poślizg międzyzębny może wywiązywać się jedynie wzdłuż prostych linii stycznych do współpracujących ze sobą zębów kół. Są to proste tworzące geometryczną powłokę - hiperboloidę. Stosowane w technice przekładnie hipoidalne zawsze mają zarysy kół jedynie przybliżone do kształtów hiperboloid. Mówiąc o względnych poślizgach współpracujących kół będziemy mieć na myśli zarys teoretyczny, w którym proste, tworzące hiperboloidę, są stycznymi do zarysu rzeczywistego. Poślizg rzeczywisty zębów zachodzi zawsze wzdłuż prostych teoretycznych tworzących hiperboloidę. Normalne obciążenie międzyzębne przekazuje się na kierunku prostopadłym do prostych tworzących.

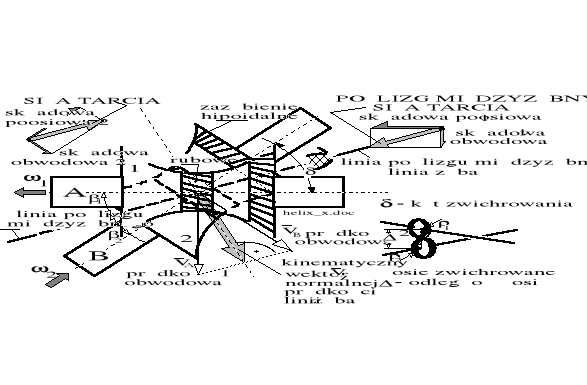
Rysunek 5.3. Zestawienie dwóch kół hiperboloidalnych przy dowolnej wartości kąta między zwichrowanymi osiami. Odległość osi = 1 + 2.

5.2. Podstawowe zależności kinematyczne.

Prosta, tworząca wspólne zazębienie dla obydwóch kół, ma określoną prędkość postępową ściśle prostopadłą do jej kierunku. Prędkość ta jest więc wspólna dla obydwóch kół. Wektor tej prędkości leży na wspólnej płaszczyźnie obwodowo stycznej do obydwóch kół, na której też leży prosta tworząca wspólne zazębienie.

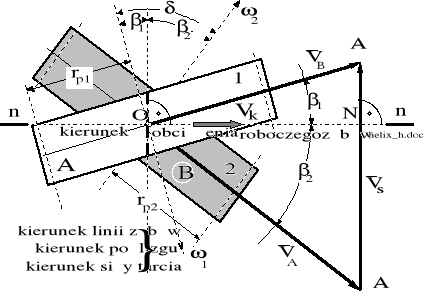
Rysunek 5.4. Przypadek współpracy kół walcowo - śrubowych realizujących transmisję momentu w przekładni hipoidalnej. Vk - normalna prędkość zarysu zazębienia.

W przekładni hipoidalnej, zgodnie z wcześniejszymi uwagami, wzdłuż prostej linii zęba zachodzi poślizg międzyzębny, który będziemy - w dalszym ciągu - nazywać poślizgiem hipoidalnym. Termin ten został wprowadzony dla odróżnienia poślizgu właściwego jedynie przekładniom o osiach zwichrowanych, od "klasycznego" poślizgu promieniowo - obwodowego właściwego profilowi zazębienia. W dalszym ciągu poślizg promieniowo - obwodowy będziemy określać jako poślizg zarysu zęba. [W przekładniach płaskich i kulistych (walcowych i stożkowych), niezależnie od kształtu podłużnej linii zębów, poślizg hipoidalny nie występuje]. Na początek rozważymy zagadnienia kinematyczne i obciążeniowe dotyczące poślizgu hipoidalnego.

Prędkość poślizgu hipoidalnego, zgodnie z rysunkiem 5.4, jest wektorowo opisana jako różnica prędkości obwodowych
Prędkości obwodowe skośnie zazębionych kół są - w ogólnym przypadku - różne. Mają one jednak ścisłe odniesienie do (wspólnej) prędkości linii zazębienia VK:

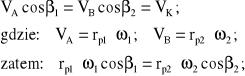
(5.1)

Przełożenie przekładni będziemy wyrażać jako stosunek prędkości obrotowej wału napędzającego (aktywnego) do prędkości obrotowej wału napędzanego (biernego). Na mocy (5.1) możemy więc napisać:

(5.2)

Odległość osi wyraża się następująco:

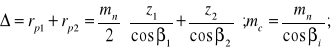
(5.3)

gdzie: mc - moduł czołowy; mn - moduł normalny (narzędzia) zazębienia.

z1, z2, - liczby zębów - odpowiednio - koła aktywnego i biernego.

rp - promień podziałowy lub toczny w zazębieniu niekorygowanym.

Prędkość poślizgu, rozumiana jako moduł wektora, jest opisana następująco:

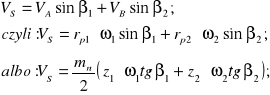
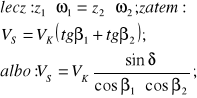
(5.4)

W stosunku do prędkości obwodowej koła aktywnego (numer 1), prędkość wzdłużnego poślizgu zębów wyraża się szczególnie prosto:

5.3. Obciążeniowe i sprawnościowe implikacje poślizgu hipoidalnego.

Jako wymienione implikacje będziemy traktować zależności opisujące przekazywanie zarówno momentu napędowego jak i mocy napędowej z koła aktywnego (napędzającego) na koło bierne (napędzane). Występujące w przekładni hipoidalnej dodatkowe poślizgi, na skutek nieuchronnych sił tarcia przynoszą straty wartości transmitowanego momentu napędowego oraz obniżają energetyczną sprawność tej transmisji. Przykładową ilustrację rozkładu sił towarzyszących transmisji momentu z wału A na wał B, przedstawiono na rysunku 5.5.

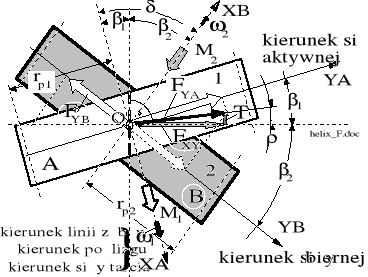
Rysunek 5.5. Ilustracja statycznej równowagi sił w punkcie (lewozwojnego) zazębienia przekładni hipoidalnej ze względu na obciążenia wałów A i B określonymi momentami M1 i M2.

Podczas ruchowej transmisji momentu napędowego z koła aktywnego 1 na koło bierne 2 uaktywnia się siła tarcia T działająca na koło aktywne zgodnie z kierunkiem prędkości względnego poślizgu w kierunku zgodnym z linią zęba. Siła tarcia T, wraz z siłą normalną do zarysu FXY, daje (zaczernioną na rysunku) wypadkową odchyloną o kąt tarcia = arctg od kierunku normalnego w kierunku koła aktywnego.

FYA - siła obwodowa na kole aktywnym rozumiana jako reakcja na moment M1.

FXY - statyczna siła normalna panująca w zarysie obciążonej pary zębów.

FYB - siła obwodowa na kole biernym określająca moment M2 na wyjściu z przekładni.

T - składowa "hipoidalna" siła tarcia międzyzębnego wzdłuż linii zęba.

Dla wyznaczenia wartości siły obwodowej FYB koła B przekazywanej podczas ruchu przekładni z koła aktywnego na koło bierne i określającej moment bierny M2=FYBrp2 należy więc uwzględnić ruchową sprawność transmisji momentu. Moc na wyjściu jest obniżona w stosunku do mocy na wejściu o wartość mocy traconej na tarcie międzyzębne. W rozważanym przez nas przypadku moc jest tracona wyłącznie na pokonanie "hipoidalnej" składowej siły tarcia T z prędkością Vs.

Składowa siła tarcia T, rozumiana według rysunku 5.5, pochodzi jedynie od siły FXY.

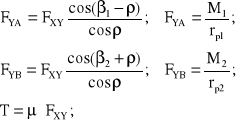
(5.5)

Wszystkie obciążenia kół opisane związkami (5.5) pochodzą od momentu aktywnego M1.

Sprawność transmisji momentu, wyznaczoną na podstawie rusunku 5.5, będziemy rozumieć klasycznie: jako stosunek mocy na wale biernym (na wyjściu, przy napędzaniu pojazdu) do mocy na wale aktywnym (na wejściu).

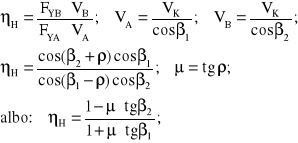
(5.6)

Wzór na sprawność przekładni możemy także wyprowadzić w inny sposób, poprzez wyznaczenie mocy traconej na tarcie.

Moc tracona PT w przekładni będącej w ruchu wynosi PT=TVs, gdzie Vs jest prędkością poślizgu "hipoidalnego", określoną związkiem (5.4) zgodnie z rysunkiem 5.4.

Hipoidalna składowa sprawności przekładni hipoidalnej złożonej z pojedynczej pary współpracujących ze sobą kół, wyraża się, podobnie jak w (5.6), następująco:

(5.7)

Zgodnie z (5.5) i (5.4) możemy napisać:

(5.8a)

Korzystając dalej z (5.5) i (5.1) otrzymujemy:

(5.8b)

skąd bezpośrednio, po podstawieniu (5.8) do (5.7), w wyniku elementarnych przekształceń, otrzymujemy ponownie postać związku (5.6).

W tym miejscu należy rozważyć praktyczne zagadnienie optymalizacyjne: jak podzielić kąt pomiędzy 1 i 2 aby hipoidalna składowa sprawności przekładni była możliwie najwyższa. W tym celu wyznaczymy warunki spełnienia minimum mocy PT traconej na tarcie. To minimum, według (5.8b), jest osiągnięte gdy:

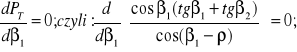
(5.9)

Powyższa pochodna zeruje się gdy spełnia się równość następująca:

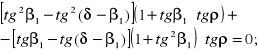
Po elementarnych przekształceniach otrzymujemy inną postać powyższej równości:

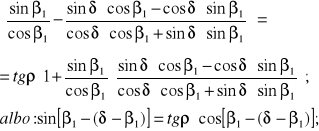
Ostatecznie mamy dwa następujące warunki określające minimum mocy tarcia: geometryczny i energetyczny:

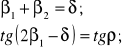
(5.10)

Warunki te są spełnione, gdy:

(5.11)

Z powyższego widzimy, że różnica kątów pochylenia linii śrubowej na kole aktywnym (napędzającym) i na kole biernym (napędzanym) powinna być równa kątowi tarcia:

(5.12)

Powyższa zasada konstrukcji optymalnej pod względem sprawności dotyczy tylko ruchu trakcyjnego podczas napędzania pojazdu. Podczas hamowania pojazdu silnikiem sprawność przekładni jest mniejsza niż przy napędzaniu.

(5.13)

5.4. Zagadnienie samohamowności przekładni (ogólnie) hipoidalnej.

Należy zauważyć, zgodnie z rysunkiem 5.5 i wyrażeniami (5.6), że wpływ kątów 1 i 2 oraz współczynnika tarcia jest na sprawność transmisji momentu bardzo znaczny. Może tak się zdarzyć, że cała moc na wejściu do przekładni zostanie zużyta na pokrycie niezbędnej mocy tarcia podczas ruchu tej przekładni. Wtedy żadnego momentu (i mocy) na wyjściu nie otrzymamy.

Zależność określająca graniczne warunki ruchowej użyteczności przekładni jest, na mocy (5.7), bardzo prosta:
Widzimy że jest to zależność ruchowa a nie statyczna. [Omawiana tu sprawność powinna nadal być rozumiana wyłącznie jako "hipoidalna" składowa sprawności ogólnej].

Graniczne warunki samohamowności - niesamohamowności należy więc określić statycznie. Aby na którekolwiek koło przekładni było możliwe przekazanie momentu napędowego to - według rysunku 5.5 - musi być spełniony podstawowy warunek niesamohamowności:

(5.14)

Widzimy że zakres niesamohamownych wartości kąta , odmierzanego od płaszczyzny koła, jest dość znaczny. Przykładowo, przy współczynniku tarcia wynoszącym 0,1 graniczna wartość wynosi aż 84,29. Dobrze jest jednak stosować kąty jak najmniejsze.

W tym miejscu należy wspomnieć o szczególnej odmianie przekładni hipoidalnej jaką stanowi przekładnia ślimakowa. W przekładni ślimakowej na ogół niewielki kąt S pochylenia linii śrubowej ślimaka należy rozumieć jako dopełnienie do 90 kąta 1:

Sprawność ruchowa przekładni ślimakowej zgodnie z (5.6) jest szczególnie niska albowiem kotangens kąta pochylenia linii śrubowej ślimaka rośnie gwałtownie z dalszym spadkiem jego zazwyczaj niewielkich wartości.

(5.15)

Stosowane w technice przekładnie ślimakowe, ze względów bezpieczeństwa, bardzo często charakteryzują się samohamownością statyczną według (5.7) pomimo, że niska sprawność ruchowa według (5.15) wpływa niekorzystnie na rozchody energii i tempo zużycia urządzenia. Jako przykład można wymienić napęd kolejek zębatych. Nawet przy równoczesnej awarii silnika i hamulców, taka kolejka nie zacznie samoczynnie staczać się po pochyłości.

Na mocy wzoru (5.6) lub (5,15) łatwo można zaprojektować przekładnię hipoidalną o określonej sprawności. W technice często korzysta się z cechy asymetrii niesamohamowności ruchowej w różnych kierunkach.

Niesymetria sprawności ruchowej wynika wprost z (5.6). Poniżej przedstawiono wzór opisujący hipoidalną składową sprawności przekładni hipoidalnej w warunkach odwrotnego kierunku przepływu mocy przy hamowaniu: od wału biernego 2 do wału czynnego 1, co ma miejsce w samochodach podczas zjazdu po pochyłości.

(5.16a)

Gdyby 1 < 2 to tg1 < tg2; zatem w warunkach ruchu "N" czyli "napędzanie kół silnikiem" według (5.6) mielibyśmy mniejszą sprawność niż w ruchu "H" - "napędzanie silnika kołami" według (5.11) i (5.16). Współczynnik asymetrii sprawności = N(nap)/H(ham) osiągnąłby wtedy wartość mniejszą od 1:

(5.16b)

Dobrze jest, gdy 1; Gdy jednakże 1, wbrew zasadzie (5.11), rośnie nadmiernie kosztem 2, to układ przekładni hipoidalnej, odpowiednio tracąc sprawność zgodnie z (5.15), zbliża się do postaci ślimakowej.

Przykładem technicznych zastosowań asymetrii sprawności niesamohamownej przekładni jest więc takie jej projektowanie dla samochodu aby przy trakcyjnej pracy napędowej sprawność ruchowej transmisji momentu była w obydwóch kierunkach wysoka lecz przy hamowaniu silnikiem zapas niesamohamowności statycznej nieco mniejszy, wspomagając pracę hamulców (niestety kosztem zwiększonego nagrzewania przekładni) na trasach górskich.

Rysunek 5.6 stanowi ilustrację pozwalającą na ogólne przedstawienie obciążeń panujących w wieńcu dowolnego koła hipoidalnego.

Schemat ogólny może stanowić podstawę analizy przypadków szczególnych:

- W przypadku śruby lub ślimaka kąt = 0; nakrętka może być traktowana jako ślimacznica o promieniu równym nieskończoności.

- Jeśli osie (przybliżonych) tworzących stożków podziałowych przecinają się w jednym punkcie to mamy do czynienia z klasyczną przekładnią stożkową (o zębach prostych lub łukowych); średnie kąty obydwóch kół muszą być odpowiednio sobie równe pod względem wartości lecz przeciwnie skierowane pod względem kierunku zwojności. Kąt pomiędzy osiami przekładni stożkowej stanowi sumę wierzchołkowych kątów tworzących stożki przybliżone: δ

- Jeśli kąty pochylenia zębów i (i=1,2) obydwóch kół nie mają odpowiednio jednakowych wartości bezwzględnych to mamy do czynienia z przekładnią hipoidalną, spiroidalną lub ślimakową.

- Poślizg hipoidalny i odpowiadająca mu składowa sprawność hipoidalna dotyczą wyłącznie przekładni hipoidalnych (wraz z przekładniami ślimakowymi).

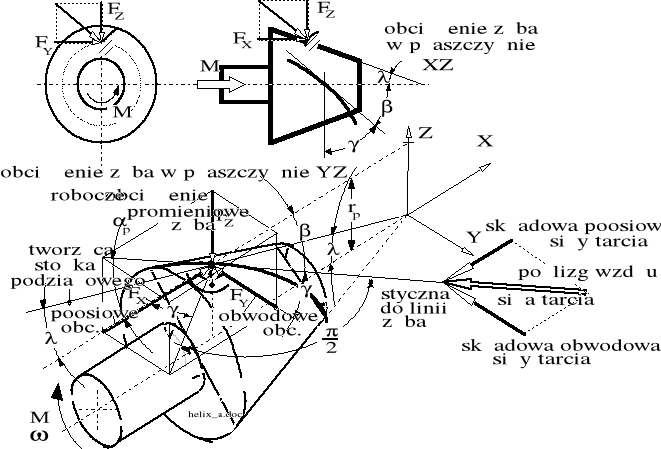
Rysunek 5.6. Ogólny schemat obciążenia koła hipoidalnego. - kąt odchylenia tworzącej średniego (przybliżonego) stożka podziałowego od osi koła. Przybliżony stożek podziałowy jest pierścieniowo styczny do hiperboloidy obrotowej na średnim promieniu podziałowym.

5.5. Poślizg i sprawność zarysu.

Poślizg, o którym będzie mowa w niniejszym podrozdziale, należy traktować wyłącznie jako promieniowo - obwodowy.

W przekładniach walcowych (o zębach prostych, śrubowych, daszkowych lub łukowych) wektor prędkości poślizgu leży w płaszczyźnie pracy przekładni.

W przekładniach stożkowych (o zębach prostych, skośnych, lub łukowych) wektor prędkości poślizgu jest styczny do sfery kulistej, której promień, jednakowy dla obydwóch kół, jest określony przez średni promień zazębienia.

Dyskusję implikacji sprawnościowych przeprowadzimy na przykładzie przekładni płaskiej. Budowę zarysu ewolwentowego zęba przedstawiono na rysunku 5.7. Schemat przekładni płaskiej o ewolwentowym zarysie zębów przedstawiono na rysunku 5.8.

Współrzędne Xz i Yz zarysu ewolwentowego koła według rysunku 5.7 wyrażają się następująco:

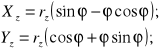
(5.17)

skąd, po elementarnych działaniach, otrzymujemy bezpośrednio:

(5.18)

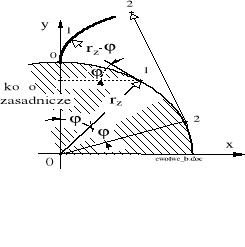
Rysunek 5.7. Ewolwentowy zarys zęba. Geometryczne zależności podstawowe;

rz - promień koła zasadniczego.

Elementarna, mierzona po ewolwencie, długość łuku wynosi:

Całkowita, mierzona od koła zasadniczego, długość łuku ewolwenty jest następująca:

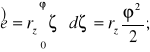
(5.19)

Z powyższego widzimy, że długość łuku przyrasta kwadratowo w funkcji kąta . Wyraźny przyrost tej długości przy podwojeniu kąta został pokazany na rysunku 5.7.

Prędkość punktu styku wędrującego po pojedynczej ewolwencie ku jej wierzchołkowi wynosi:

(5.20)

Przy współpracy dwóch kół punkt styku zębów wędruje ku ich wierzchołkom, zgodnie z rysunkiem 5.8. Prędkość poślizgu jest skierowana ku wierzchołkowi zęba. Na rysunku przyjęto następujące oznaczenia:

FOAS - statyczna siła obwodowa na tocznym kole aktywnym; MA=FOASrt1

FOAR - siła obwodowa ruchowa koła aktywnego, uwzględniająca wpływ przeciwnie skierowanej składowej siły tarcia międzyzębnego, równoważąca się z obciążeniem koła biernego; = arctg.

FOB - siła obwodowa na tocznym kole biernym;

FN - siła normalna do zarysu skierowana wzdłuż linii przyporu, wywołująca siłę międzyzębnego tarcia podczas ruchu przekładni.

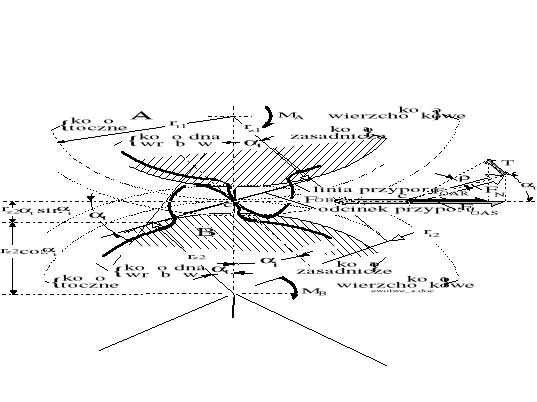
Rysunek 5.8. Schemat współpracy dwóch kół zębatych o zarysie ewolwentowym.

Prędkość poślizgu względnego w punkcie współpracy zarysów zębów jest sumą prędkości odpowiadających obydwu zarysom, przy czym przyrosty kąta obrotu poszczególnych kół są sprzężone zależnością kinematyczną (5.2) jaką jest przełożenie przekładni:

(5.21)

gdzie: rz - promień koła zasadniczego;

rt - promień koła tocznego według rysunku 5.8.

Wielkości rz i rt, według rysunku 5.8 oraz wzoru (5.14), są wzajemnie związane następującą zależnością:

gdzie: zgodnie z rysunkiem 5.8 kąt t jest tocznym czołowym kątem przyporu który, w przypadku braku promieniowego przesunięcia zarysów (korekcji), jest także podziałowym kątem przyporu. W odniesieniu do przekładni hipoidalnej we wzorze (5.21) występuje wyłącznie normalny kąt przyporu.

Biorąc powyższe pod uwagę możemy napisać wzór opisujący wypadkową, (ku-wierzchokowo skierowaną), prędkość poślizgu zębów wzdłuż ich współpracujących zarysów.

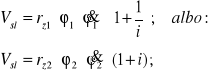
(5.22a)

Korzystając z (5.2) możemy także napisać inną postać wzoru (5.22a):

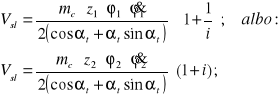
(5.22b)

gdzie: mc - moduł czołowy zęba albo moduł toczny;

mn - moduł normalny albo moduł narzędzia.

Zgodnie z powyższym wartość kąta pochylenia linii śrubowej zęba (w kole walcowym albo stożkowym) ma jedynie pośredni wpływ na międzyzębny poślizg zarysu. W kole hipoidalnym wartość ta ma wpływ jedynie na poślizg hipoidalny zaś w poślizgu zarysu w ogóle udziału nie bierze.

Składowe: obwodowa i promieniowa prędkości względnego poślizgu w obrębie zarysu zębów (pracujących na odcinku przyporu) mogą być wprost wyrażone według (5.22b) przez wstawienie - odpowiednio - wyrazu: sini albo

cosi.

Nieliniowy charakter prędkości poślizgu według (5.22), w przypadku dalszej analizy sprawności z uwzględnieniem siły tarcia, nie ma żadnego znaczenia bowiem siła tarcia, z dobrym technicznym przybliżeniem, zależy od znaku prędkości a nie od wartości tej prędkości.

Sprawność zarysu.

Dla wyznaczenia sprawności zazębienia, zależnej wyłącznie od zjawiska poślizgu zarysu, na podstawie rysunku 5.8 sporządzimy zapis bilansu sił obwodowych w ruchu przekładni:

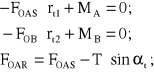
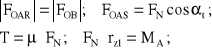
(5.23)

Sprawność zarysu, rozumiana klasycznie jako stosunek mocy na wyjściu z zazębienia do mocy na wejściu, wyraża się następująco:

(5.24a)

Prędkość Vc punktu "c" (rys. 5.8) jest wspólna dla obydwóch kół.

Wobec powyższego składowa "sprawność zarysu" wyraża się wzorem następującym:

(5.24b)

Składowa "sprawność hipoidalna", zgodnie z (5.6), wyraża się następująco:

(5.25)

5.6. Sprawność całkowita zazębienia pojedynczej pary kół, w ogólnej postaci wykonania przekładni zębatej, wynosi:

(5.26)

Sprawność przekładni hipoidalnej nie zależy od rodzaju zastosowanych w niej kół: walcowych lub stożkowych. Wzdłużna prędkość poślizgu międzyzębnego, na całej długości prostej tworzącej hiperboloidę obrotową, zgodnie z (5.4) i (5.1), jest taka sama i niezależna od szczegółowej geometrycznej postaci koła. Tym samym trakcyjna przekładnia stożkowa może być w pełni ekwiwalentna w stosunku do przekładni walcowej. Na rysunku 5.3 pokazano współpracę kół hipoidalnych. Wybór technicznej, przybliżonej do hiperboloidy teoretycznej, postaci kół należy do konstruktora. W napędach trakcyjnych, z przyczyn wytrzymałościowych, konstruktorzy stosują koła stożkowe. Przy transmisji momentu bowiem siła obwodowa FO maleje ze wzrostem promienia. Koło stożkowe tej samej hiperboloidy teoretycznej ma zawsze większy promień od koła walcowego i odpowiednio mniejsze siły obwodowe: FOSrS=FOWrW.

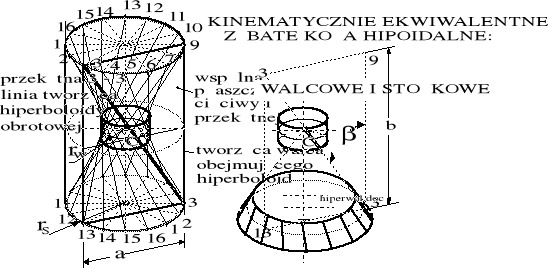
Rysunek 5.9. Kinematycznie ekwiwalentne koła hipoidalne: walcowe i stożkowe.

5.7. Kinematycznie i sprawnościowo ekwiwalentne postacie przekładni.

Rysunki 5.3, 5.6 i 5.9 ilustrują przestrzenne pojmowanie kąta w kole walcowym lub stożkowym przekładni hipoidalnej, stosownie do przytoczonych i analizowanych wzorów. Wszystkie wzory wyprowadzono według ilustracji sporządzonych dla przypadku hipoidalnej przekładni z kołami walcowymi. Jak jednak wspomniano w komentarzu przed rysunkiem 5.9, koła stożkowe mają mniejsze obciążenia obwodowe co dla konstruktorów przekładni trakcyjnych ma poważne, niekiedy decydujące, znaczenie.

Na rysunku 5.10 przedstawiono przestrzenną postać linii współpracy zębów dwóch kół. Prosta "p", jest wspólną dla obydwóch kół linią współpracy zębów niezależnie od tego czy koła są walcowe czy stożkowe.

Rysunek 5.11 szczegółowo przedstawia wymiary hipoidalnej przekładni, w obrębie zarówno kół walcowych jak i stożkowych, niezbędne dla wyprowadzenia analitycznych zasad geometrycznej ekwiwalentności.

Przy projektowaniu przekładni hipoidalnej konstruktor najczęściej przyjmuje następujące warunki wyjściowe:

- odległość osi ;

- przełożenie przekładni i =A/B;

- kąt pomiędzy osiami wałów .

Przyjęcie zasady podziału kąta pomiędzy poszczególne koła zgodnie z (5.11) lub (5.16b) stanowi pierwszy krok w procesie projektowania przekładni.

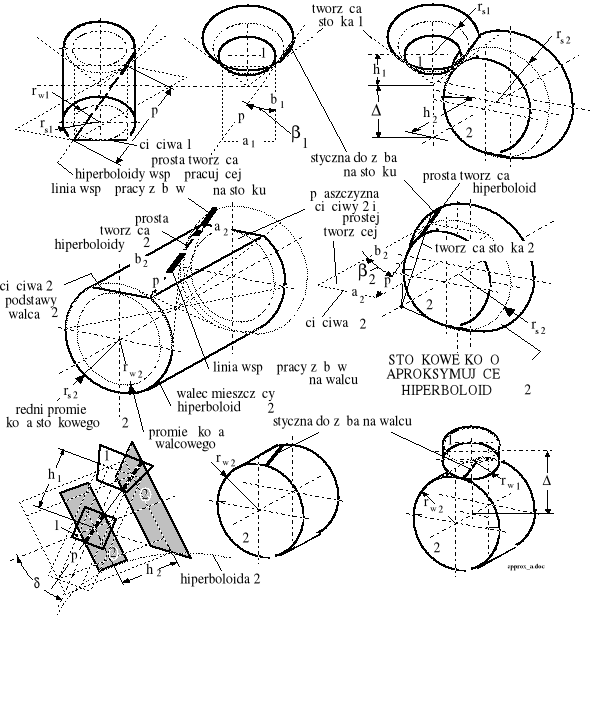
Rysunek 5.10. Schemat przestrzennej konfiguracji wzajemnej prostokreślnych hiperboloid obrotowych według rysunków 5.3 i 5.9.

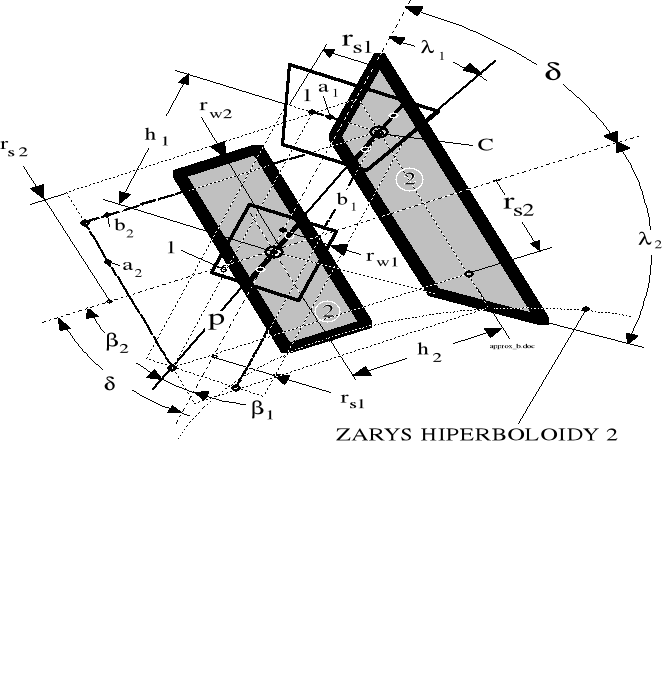
Rysunek 5.11. Wymiary charakterystyczne przekładni hipoidalnej.

Drugim krokiem jest wybór stopnia redukcji obciążeń obwodowych przy zwiększeniu średniego promienia koła stożkowego rS w stosunku do promienia koła walcowego rW. Jest to wytrzymałościowy problem kół zębatych, nie objęty tematem niniejszej książki. W przypadku decyzji o konstrukcyjnej redukcji obciążenia obwodowego, relacja rS/rW określa wymiary geometryczne całej przekładni. Zgodnie bowiem z rysunkami 5.9, 5.10 i 5.11, przy kołach stożkowych obowiązują, względem kół walcowych, następujące zależności:

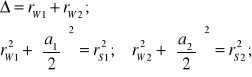
(5.27)

Ponieważ wartości kątów 1 i 2 zostały już określone w pierwszym kroku postępowania projektowego to na mocy związków (5.27), zgodnie z rysunkami 5.10 i 5.11, możemy też określić podstawowe wymiary kół stożkowych:

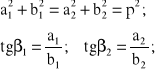
(5.28)

(5.29)

Po wyznaczeniu wymiarów kół stożkowych: średnich promieni rS1, rS2 i wierzchołkowych kątów pochylenia tworzących 1 oraz 2 w stosunku do osi stożków, geometria hipoidalnej trakcyjnej przekładni stożkowej, ekwiwalentnej w stosunku do przekładni walcowej, została określona w stopniu stanowiącym punkt wyjścia do obliczeń wytrzymałościowych. W tym miejscu należy jednak pamiętać że wartości średnich promieni rsi (i=1,2) na stożkach podziałowych, według (5.29) i (5.2), są ściśle zależne zarówno od liczb zi zębów kół jak i od kątów i pochylenia linii zębów w tych kołach:

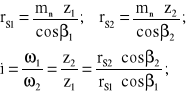
(5.30)

Gdzie: mn - moduł normalny zębów na średnim promieniu koła stożkowego.

W praktyce projektowej, gdy 12, należy się więc liczyć z koniecznością nieuchronnego kompromisu pomiędzy nienaruszalnością wyjściowego wymiaru oraz zachowaniem wartości kątów i gwarantujących najwyższą obliczeniową sprawność przekładni. Problem znika jedynie wtedy, gdy 1=2;

Obliczeniowe reguły geometrycznej ekwiwalentności kinematyki kół walcowych i stożkowych przekładni hipoidalnej można przedstawić następująco:

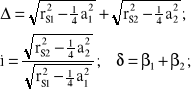
(5.31)

Gdzie: rsi (i=1,2) - średni promień mierzony na podziałowym stożku uogólnionym. W przypadku kół walcowych a1=a2=0.

Stopień redukcji siły obwodowej hipoidalnych kół stożkowych FOS w stosunku do kół walcowych FOW wynosi:

(5.32)

Wykres hipoidalnej składowej sprawności przekładni, w zależności od wartości kątów 1 i 2, przedstawiono na rysunku 5.12. W obliczeniach do wykresu przyjęto: =0,0875; =5; =90; t=20; Maksimum składowej hipoidalnej sprawności według (5.25) wynosi 0,8396; Sprawność zarysu według (5.24) wynosi 0,968; Najwyższa sprawność przekładni, będąca iloczynem tych sprawności składowych, wynosi więc 0,813. Niemal dziewiętnaście procent mocy transmitowanej przez przekładnię hipoidalną jest zamieniane na strumień ciepła. W przekładni stożkowej tylko 3,2%.

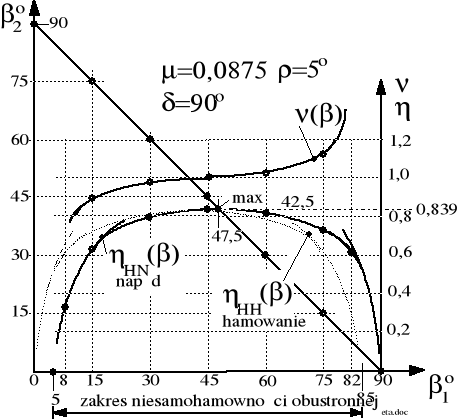
Rysunek 5.12. Wykres hipoidalnej składowej sprawności przekładni HN() oraz współczynnika asymetrii sprawności () w funkcji kąta 1. Współczynnik tarcia =0,0875.

5.8. Literatura źródłowa:

[1] Ochęduszko K.: Koła zębate. PWT Warszawa. 1959

[2] Shigley J.E., Mitchell L.D.: Mechanical engineering design. Mc Graw - Hill 1983.

[3] Oderfeld J.: Wstęp do mechanicznej teorii maszyn WNT Warszawa, 1962.

56

---