CZĘŚĆ III: TRANSMISJA MOMENTU TRAKCYJNEGO

POMIĘDZY OSIAMI WZGLĘDEM SIEBIE RUCHOMYMI

Rozdział 8.

MECHANIZMY KOMPENSACJI NIEWSPÓŁOSIOWOŚCI W NAPĘDACH TRAKCYJNYCH

8.1. Trakcyjny napęd łańcuchowy z kompensacją niewspółosiowości.

Napęd łańcuchowy pojazdów jednośladowych, motocykli i rowerów, jest znany powszechnie. Jego szeregowa struktura mechaniczna jest czytelna w sposób oczywisty, gdyż napędzane jest tylko jedno koło pojazdu.

Rozważymy mechanikę napędu łańcuchowego gdy usprężynowane tylne koło pojazdu jest w prowadzone ramie za pomocą wahacza o promieniu R, wahliwie osadzonego w jego gnieździe obrotu. Napęd trakcyjny jest transmitowany na koło napędowe od zębatki silnika osadzonego w ramie pojazdu. Podstawowe wymiary geometryczne układu przedstawiono na rysunku 1.

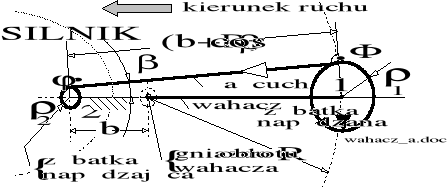
Rysunek 8.1. Układ łańcuchowego napędu koła motocykla w pozycji "zerowej", przed narzuceniem obrotu wahacza w gnieździe.

Oznaczenia: - kąt pochylenia cięgna (łańcucha);

b - odległość osi zębatki napędzającej i gniazda wahacza;

R - promień wahacza;

- promień zębatki łańcuchowej

1, 2 - indeksy odnoszące się do zębatek koła i silnika;

i - przełożenie przekładni łańcuchowej.

Jako wielkości stałe, charakteryzujące geometrię i kinematykę analizowanego układu, przyjmijmy następujące współczynniki - parametry tego układu:

(8.1)

Z chwilą narzucenia obrotu wahacza o kąt , konfiguracja układu zmienia się. Odległość osi zębatek nieco się zmniejsza o wielkość l: z początkowej wartości (b+R), do wartości W "na przełaj" w nowym położeniu. Zmienia się też czynna długość łańcucha. Także początkowa wartość kąta nachylenia łańcucha w stosunku do prostej łączącej środki obydwóch zębatek nieznacznie się zmienia. Nowy układ geometryczny napędu łańcuchowego pokazano na rysunku 8.2.

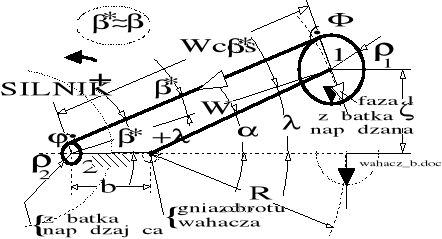
Rysunek 8.2. Układ łańcuchowego napędu koła motocykla po narzuceniu obrotu wahacza w lewym kierunku, ku górze.

Obrót wahacza zachodzi w lewo lub w prawo, zawsze w otoczeniu położenia "zerowego". Przykładowo rozważymy obrót w lewo. Kierunek obrotu w lewo będziemy dalej traktować jako dodatni.

Dla sporządzeniu zapisu następstw zmiany geometrycznej konfiguracji układu będziemy przyjmować, że początkowe kątowe położenie zębatki napędzanej "1", po narzuceniu obrotu ramienia wahacza o kąt pozostało niezmienione, co pokazano na obydwóch rysunkach przez naniesienie znacznika.

Odnośnie kąta pochylenia osi cięgna - łańcucha w stosunku do prostej łączącej środki zębatek możemy napisać:

(8.2)

W praktyce, z dobrym przybliżeniem można przyjmować, *.

Należy zauważyć, że przy niezmienionym położeniu kątowym zębatki napędzanej, skróceniu aktywnej części łańcucha o wielkość l towarzyszył dodatkowy obrót aktywnej zębatki silnika w lewo o kąt l.

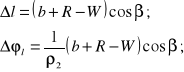
(3)

Równocześnie także wystąpił obrót zębatki silnika wywołany obrotem wahacza. Obrót ten możemy sobie wyobrazić w dwóch fazach. W fazie pierwszej, zębatka napędzana "1", pozostając w pozycji obrotowo unieruchomionej w stosunku do ramienia wahacza, wywołuje obrót zębatki silnika "2" w lewo o kąt tak, jakby łańcuch był sztywnym prętem, przyłączonym przegubowo do obydwóch zębatek na ich promieniach. W fazie drugiej, przywracamy początkowe, pionowe położenie znacznika zębatki "1" przez obrót tej zębatki w prawo o kąt . Tym samym, także zębatka "2" obróci się w prawo lecz o kąt odpowiednio większy, wynikający ze stosunku promieni obydwóch zębatek.

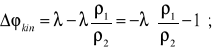
(8.4)

Wypadkowy obrót zębatki silnika "2", wynikający wyłącznie z uniesienia koła motocykla w stosunku do ramy o wielkość , czyli wynikający z obrotu wahacza, jest sumą wyżej opisanych kątowych przemieszczeń składowych:

(8.5)

W dalszym ciągu będziemy korzystać z rozwinięć funkcji trygonometrycznych w szereg ograniczając się do uwzględnienia argumentu w potędze co najwyżej drugiej.

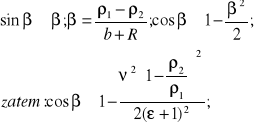
(8.6)

i podobnie:

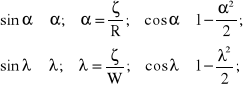
(8.7)

Wielkość W możemy wyznaczyć porównując dwa prostokątne trójkąty występujące na rysunku 8.2, których jedną przyprostokątną - w obydwóch przypadkach - stanowi wielkość , zaś przeciwprostokątną jest kolejno R i W.

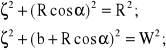
(8.8)

Po wykonaniu elementarnych przekształceń z wykorzystaniem oznaczeń (8.1), otrzymujemy:

(8.9)

Na mocy (8.3), korzystając z (8.6) i (8.9), możemy otrzymać zapis pierwszej składowej dodatkowego obrotu zębatki "2" silnika:

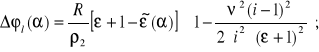
(8.10)

Pierwsze po prawej stronie znaku równości wyrażenie w nawiasie kwadratowym, po uwzględnieniu zapisu (8.9), może zostać przekształcone do znacznie prostszej postaci według (zamieszczonych w każdym poradniku matematyki wyższej) zasad rachunku przybliżonego:
Wzór ten zapewnia dokładność poniżej 1%, gdy -0,247a2<x<0,328a2, co w omawianym przypadku technicznym, zawsze jest spełnione. Postępując według powyższego schematu, otrzymujemy:

(8.11)

Druga składowa obrotu zębatki "2", zgodnie z (8.4), (8.7) i (8.9), zawiera
w mianowniku:

(8.12)

W tym przypadku rachunek przybliżeń przynosi wzór następujący:

który także zapewnia dobrą dokładność, poniżej 1%, gdy: 0,157a2<x<0,166a2, co, podobnie jak poprzednio, w omawianym przypadku technicznym, zawsze jest spełnione. Postępując według powyższego schematu, przy zachowaniu wyrazów zawierających w potędze co najwyżej drugiej, otrzymujemy kolejno:

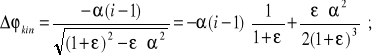
(8.13)

Całkowity obrót zębatki silnika jest opisany wzorem (8.5), przy wykorzystaniu (8.10), (8.11) i (8.13). Otrzymujemy więc ostatecznie:

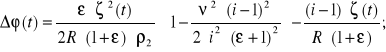
(8.14)

Teraz jest miejsce na zwięzłą dyskusję jakościową transmisji momentu. W ruchu pojazdu po nierównościach drogi zarówno wielkość =(t) jak też wielkości , , W, , są funkcjami czasu. Z punktu widzenia transmisji momentu trakcyjnego zmienna w czasie wartość stanowi źródło zaburzeń dynamicznych w układzie napędowym i powoduje zarówno niszczenie mechanicznego układu transmisji momentu jak też sprawia, że pokonywane nierówności drogi, w sposób nieuchronny, odwzorowują się dynamicznie w szkodliwych zaburzeniach prędkości zarówno samego silnika jak też całego pojazdu.

Oznaczając
otrzymujemy wzór opisujący kątowe zaburzenie prędkości zębatki silnika w funkcji zaburzeń położenia i prędkości koła pojazdu. W podobny sposób możemy otrzymać zapis sprzężenia przyspieszeń.

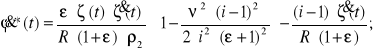
(8.15)

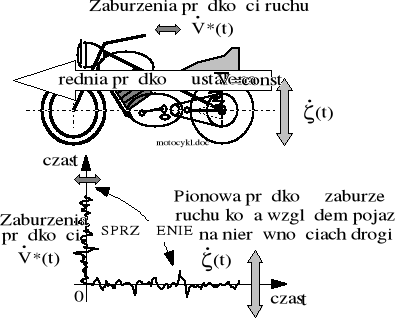
Rysunek 8.3. Pojęciowa ilustracja sprzężenia pionowych prędkości ruchu koła względem ramy z teoretycznymi zaburzeniami prędkości ruchu pojazdu.

Sprzężenie zaburzeń pionowego położenia koła względem ramy w ruchu pojazdu po nierównościach drogi (t) z wielkością opisującą zmianę obrotowego położenia zębatki silnika, według rysunku 8.2 i wzoru (8.14), będziemy nazywać funkcją położenia przekładni łańcuchowej. Każde zaburzenie kątowego położenia zębatki silnika wywołuje zaburzenie położenia w ruchu całego pojazdu. To samo dotyczy prędkości i przyśpieszeń. Oczywiście, całkowite uniknięcie szkodliwego sprzężenia zaburzeń obrotowego ruchu zębatki silnika z nierównościami drogi jest możliwe, gdy są równocześnie spełnione dwa warunki: i=1; oraz =0, [czyli b=0]. Tylko wtedy jest możliwy płynny, niezaburzony ruch obrotowy silnika przy dowolnej, także płynnej, niezaburzonej prędkości ruchu pojazdu poruszającego się wzdłuż drogi po jej nierównościach.

W praktyce sprzężenie to jest przez większość producentów ignorowane: w motocyklach rajdowych nikt nie troszczy się o komfort podróżowania i trwałość pojazdu; na asfalcie zaś nierówności drogi są znikome.

Istnieje jeszcze trzecia przyczyna zaburzeń ruchu układu przy napędzie łańcuchowym. Tą przyczyną jest immanentna cecha kinematycznej współpracy łańcucha Galla z zębatką.

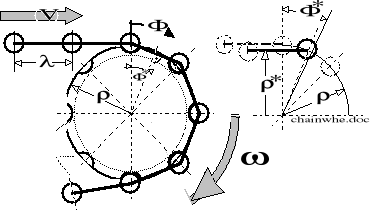
Rysunek 8.4. Schemat kinematycznej współpracy łańcucha z zębatką.

VŁ - prędkość ruchu łańcucha

Na podstawie rysunku 4, możemy napisać:

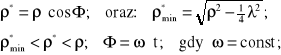
(8.16)

Promień * zmienia się w zakresie ruchu zębatki od kąta położenia -* do wartości +*. W tym zakresie kąta, przy ustalonej prędkości obrotowej zębatki, czas t zawiera się w granicach: -t*<t<+t*;

Prędkość łańcucha wynosi więc VŁ(t) =*; *=*(t); albo VŁ(t)=cost;

Prędkość średnia łańcucha wynosi:

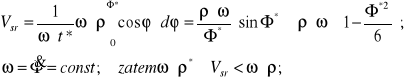
(8.17)

Omówiliśmy trzy źródła zaburzeń ruchu w układzie napędu łańcuchowego:

- obrót wahacza oraz zębatki silnika na nierównościach drogi,

- zmianę odległości osi i roboczej długości łańcucha,

- niesynchroniczną współpracę kinematyczną łańcucha z zębatką.

Zaburzenia te, występując łącznie, wzbudzają poprzeczne drgania łańcucha i stanowią przyczynę szybkozmiennych obciążeń dynamicznych, powodując hałas i zmęczeniowe zużycia elementów napędu. Obciążenia dynamiczne w znacznym stopniu są kompensowane podłużnymi, sprężystymi odkształceniami łańcucha.

169

---