8.7. Obciążenia zginające wału przegubowego

Środkowy odcinek wału przegubowego jest przyłączony do wału napędzającego oraz do wału napędzanego poprzez sprzęgła wychylne. Masa środkowego odcinka wały jest zawieszona na tych sprzęgłach.

Obciążenia środkowego odcinka wału przegubowego składają się z następujących obciążeń częściowych:

Obciążeń skręcających (roboczych) My działających w układzie transmisji momentu napędowego;

Obciążeń zginających w postaci momentów Mx i Mz działających zgodnie z kierunkami osi X i Z;

Obciążeń poprzecznych (promieniowych) Fx i Fz działających w płaszczyznach pracy sprzęgieł zgodnie z kierunkami osi X i Z. Obciążenia Fx i Fz równoważą (ogólnie niezrównoważony) układ momentów Mx i Mz przyłożonych do obydwóch końców środkowego odcinka wału przegubowego;

Obciążeń wibracyjnych pochodzących od dynamicznego niewyrównoważenia środkowego odcinka wału przegubowego.

Dynamiczne niewyrównoważenie może mieć charakter pierwotny lub wtórny. W pierwszym przypadku, jest ono usterką wytwórczą; w drugim - ujawnia się w wyniku sprężystych odkształceń poprzecznych przy relatywnie silnym obciążeniu roboczym.

Wał przegubowy należy tak zaprojektować i dobrać jego sprzęgła, aby w warunkach roboczych odkształcenia były nieznaczne. Ponadto, sztywność wału na zginanie - i jego własne częstości drgań poprzecznych - powinny być dobrane w stosunku do prędkości roboczej tak, aby nie następowało wzbudzenie i rezonansowe wzmocnienie drgań poprzecznych wału.

Przyczyną drgań poprzecznych wału mogą też być błędy montażowe wychylnych sprzęgieł cięgnowych i krzyżakowych, zużycia elementów sprzęgieł i luzy ujawniające się przy działaniu:

- obciążeń grawitacyjnych;

- obciążeń bezwładnościowych;

Poszczególne rodzaje obciążeń w jednej płaszczyźnie przedstawiono na rysunku 8.63; (rzeczywisty układ obciążeń jest na ogół przestrzenny).

Obciążenia zginające działające w prostopadłych do osi obrotu wału płaszczyznach pracy sprzęgieł (na których zawieszony jest wał) zależą od rodzaju sprzęgieł, geometrycznej konfiguracji poszczególnych odcinków wału przegubowego oraz wartości obciążeń roboczych (skręcających) wału i sprzęgieł.

Wcześniej w p. 8.6.1, na rysunku 8.54, został przedstawiony rozkład obciążeń roboczych w sprzęgle, którego osie są załamane przestrzennie, na przykad według rysunku 8.64.

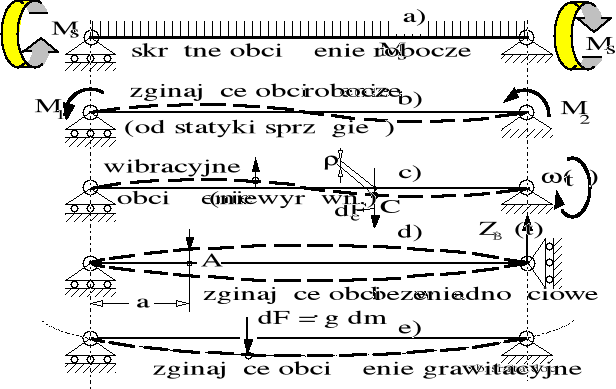
Rysunek 8.63. Zestawienie poszczególnych rodzajów obciążeń wału przegubowego. c) niewyrównoważenie; d) - ruchomy koniec wału;

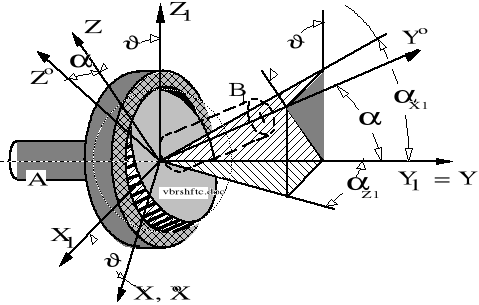
Rysunek 8.64. Przestrzenne załamanie osi wałów sprzęgła wychylnego.

Obciążenia działające zgodnie z kierunkami osi X i Z, w stosunku do obciążeń działających zgodnie z kierunkami osi X i Z (rys. 8.54) można wyznaczyć za pomocą równań statyki równowagi sprzęgła:

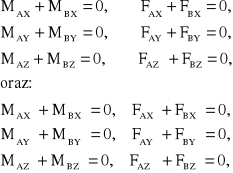
(8.174)

Znając wartości obciążeń działających zgodnie z kierunkami osi X i Z (rys. 8.54) przyporządkowuje się je kierunkom X i Z pokazanym na rysunku 8.64.

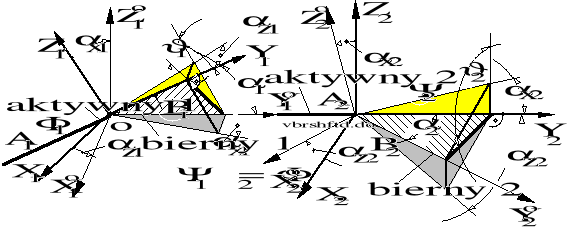
Rysunek 8.65. Przestrzenna konfiguracja wału przegubowego.

Odpowiednie wzory przyporządkowujące obciążenia znane (zgodnie z rys. 8.54) obciążeniom poszukiwanym, odpowiadającym kierunkom X1 i Z1 na rysunku 8.64, są następujące:

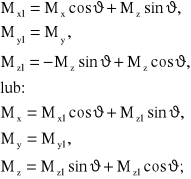
(8.175)

Układ wału płaskiego, którego osie są załamane w płaszczyźnie OYZ i OYZ, jest bowiem obrócony o kąt .

Kąty
można wyznaczyć na podstawie dokumentacji technicznej przedstawiającej mechanizm napędowy. Znając przestrzenny układ obciążeń pojedynczego sprzęgła wału przegubowego można przystępić do analizy obciążeń tego wału. Przeniesiony z dokumentacji technicznej układ geometryczny wału przedstawiono na rysunku 8.65.

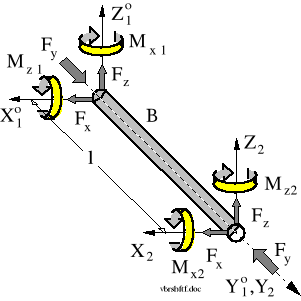
Rysunek 8.66. Obciążenie środkowego odcinka wału przegubowego.

Podstawowa struktura obliczeń jest szeregowa: od wału napędzającego do napędzanego.

Aby wyznaczyć siły promieniowe F (według rysunku 8.63) przyłożone do końcówek środkowego odcinka wału przegubowego, należy uprzednio wyznaczyć wartości momentów M1 i M2 zginających wał z obydwóch końców.

W przypadku ogólnym, momenty te nie równoważą się wzajemnie. Zgodnie bowiem z rysunkiem 8.63.b, warunek równowagi jest następujący:

(8.176)

Jeśli więc
to występują siły promieniowe F. Siły te mogą działać zarówno zgodnie z kierunkami
- zgodnie z rysunkiem 8.66.

Na rysunku 8.66
X1X2 oraz Z1Z2, podobnie jak na rysunku 8.65. Obciążenia wału przegubowego wyznacza się następująco:

(a) Wyznacza się wzajemną geometryczną konfigurację roboczą poszczególnych odcinków wału przegubowego,

(b) Wyznacza się obciążenia robocze (skręcające) poszczególnych odcinków wału,

(c) Przeprowadza się częściową analizę statyki zarówno sprzęgła 1 jak i sprzęgła 2, ze względu na momenty Mx, Mz, Mx i Mz , według wzorów (8.174),

(d) Przelicza się częściową statykę każdego sprzęgła z przypadku płaskiego na przestrzenny (rys. 8.64) według wzorów (8.175),

(e) Przeprowadza się analizę równowagi środkowego odcinka wału przegubowego zarówno w płaszczyźnie Z1,Z2, jak i X1,X2 (rys.8.65) w warunkach przyjętej konfiguracji roboczej:

- w wyniku tej analizy oblicza się wartości
działających na środkowy odcinek wału oraz reakcji tego odcinka na kierunkach X1,Y1,Z1 wału napędzającego a także X1,Y1,Z1 wału napędzanego.

(f) Wałki nawrotnika i przekładni osiowej oblicza się uwzględniając skręcające obciążenia robocze
zginające
a także siły promieniowe

(g) Środkowy odcinek wału oblicza się uwzględniając następujące obciążenia:

Układ geometryczny wału przyjęto w dalszym ciągu według rysunku 8.65.

Skręcające obciążenia robocze poszczególnych odcinków wału dla My1=const wyznaczono na podstawie przykładu zaczerpniętego z pracy [4]. Dla środkowego odcinka wału otrzymano:

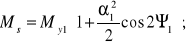
(8.177)

Przy czym 1 jest kątem obrotu środkowego odcinka wału mierzonym pomiędzy płaszczyzną widełek tego wału a osią Z1. Podobnie też wyznaczono:

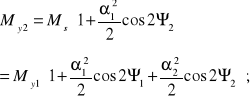
(8.178)

gdzie 2 jest kątem obrotu napędzanego odcinka wału mierzonym pomiędzy płaszczyzną widełek tego wału a osią Z2 .

Dla
w układzie występuje pulsacja momentu napędowego. Ponieważ w praktyce
zatem ze względu na wyraz
można na ogół przyjmować

W wałach specjalnych jedynie pulsacja obciążeń skręcających (8.177) odcinka środkowego wału może wywierać znaczenie zmęczeniowe, które powinno być uwzględnione w obliczeniach zmęczeniowych tego odcinka.

Jako wartość 1 należy przy tym przyjmować jmax.

Poniżej zostały podane wzory opisujące obciążenia wału biernego, dla przypadku załamania osi według oznaczeń zamieszczonych na rysunku 8.65.

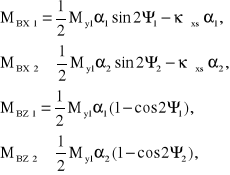
(8.179)

przy czym zs jest sztywnością sprzęgła na załamanie osi zgodnie z tablicą 8.9. zamieszczoną w poprzednim podrozdziale.

Ponieważ pulsacja momentu Ms jest w praktyce conajmniej kilkuprocentowa (w stosunku do średniego obciążenia roboczego), to zgodnie z rysunkiem Z.4.2 można przyjmować
Wówczas przyjmuje się poprzeczne momenty zginające wały łożyskowane (A1 i B2 na rysunku 8.65) jako w przybliżeniu równe co do wartości bezwzględnej momentom obciążającym zginająco środkowy odcinek wału przegubowego. Można więc napisać:

(8.180)

Podobnie też możemy napisać dalsze związki przybliżone:

(8.181)

przy czym:

W tym miejscu należy podkreślić, że wzory (8.180) opisują obciążenia przyporządkowane układowi współrzędnych związanych z wałem napędzającym A. Aby zbadać równowagę środkowego odcinka wału, należy te obciążenia obliczyć przyporządkowując je odpowiednio do układu O1X1Y1Z 1. Na podstawie (8.176), po odpowiednim uporządkowaniu indeksów, wyznacza się siły Fj; (j=x,z).

Dla pełnego obrazu analizy obciążeń wału przegubowego należy podkreślić, że na środkowy odcinek wału działają siły Fx i Fz skierowane do niego prostopadle. Siły Fy(1,2) mogą pochodzić np. od podłużnych napięć montażowych, gdy wał nie jest dzielony z możliwością wysuwnego wydłużania.

W sprzęgłach cięgnowych mogą także pojawiać się składowe poosiowe sił działających na wał. Niezależnie od tego, reakcje na siły Fx(1,2) i Fz(1,2) zawsze mają dwie składowe sił Fy(1,2) i Fz(1,2), które wchodzą w skład pełnego stanu obciążeń wałków łożyskowanych A1 i B2 (rys. 8.65).

Analizując obciążenia środkowego odcinka B wału przegubowego należy wrócić do rysunku 8.66. Zarówno w płaszczyźnie XjYj, jak też w płaszczyźnie ZjYj (zgodnie z rysunkiem (8.65) będą występowały obciążenia przedstawione na rysunku 8.67.

Momenty zginające obciążające wał przegubowy w jego środkowej części oraz charakter dynamicznych odkształceń wału jako następstwo dynamiki poprzecznej.

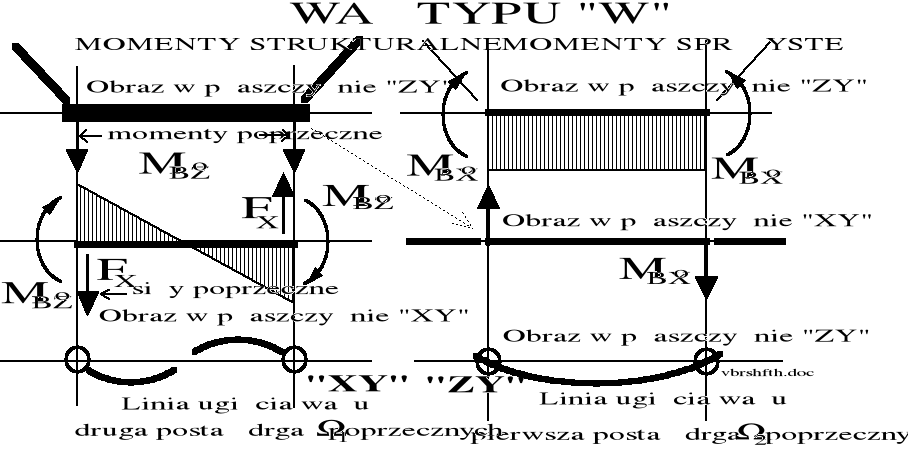
Rysunek 8.67b. Charakter dynamicznych odkształceń wału przegubowego zależnie od jego przestrzennej konfiguracji. Przykłady dwóch konfiguracji płaskich.

Pulsujące składowe obciążenia Mx1,Mz1,Mx2,Mz2 powodują, zgodnie z (8.180) i (8.181), że wirujący z prędkością kątową środkowy odcinek wału jest poddany wymuszeniom drgań giętnych z częstością 2. Wielkość występuje we wzorach (8.179) jako chwilowa wartość kąta obrotu

(8.182)

Częstość wymuszenia 2 (w ogólnym przypadku) może w środkowym odcinku wału przegubowego wzbudzać drgania poprzeczne n-tej postaci. Jednakże w pojazdach pracujących z różnymi prędkościami jazdy najbardziej niebezpieczna jest pierwsza postać drgań. Częstość odpowiadająca częstości pierwszej postaci drgań poprzecznych wału powinna być znacznie większa niż częstość 2 wymuszenia tych drgań. Ponieważ wały przegubowe pojazdów pracują w zakresie prędkości podrezonansowych, dlatego też należy je traktować jako względnie wolnoobrotowe. Tłumienie drgań w giętnie drgającym wale jest bardzo słabe.

Częstość drgań swobodnych i-tego rzędu środkowego odcinka B wału podpartego według schematu pokazanego na rysunku 8.63 opisuje następujący wzór:

(8.183)

gdzie: m- masa jednostki długości (jednorodnego modelu) wału [kg/m];

EJg - sztywność wału na zginanie [Nm2];

l - rozstaw podpór wału [m],

A - przekrój poprzeczny wału [m2],

Moment bezwładności Jg, i wskaźnik wytrzymałości Wg pierścieniowego przekroju wału na zginanie wynosi:

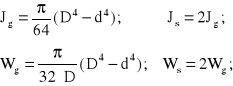
(8.184)

gdzie D i d oznaczają odpowiednio średnicę zewnętrzną i wewnętrzną przekroju kołowego pierścienia (rurowego odcinka wału środkowego).

Pulsacja sprężysto - skręcająca wału jest funkcją podwojonego kąta obrotu wału . Sztywność skrętna odcinka B wału jest opisana wzorem następującym:

(8.185)

gdzie G - moduł sprężystości postaciowej materiału, z którego jest wykonany wał,

Js - moment bezwładności przekroju wału [m4] na skręcanie (według 8.184),

l - długość odcinka B wału [m].

Oznaczając sztywności skrętne sprzęgieł jako
, wypadkową sztywność skrętną wału przegubowego można obliczyć według wzoru:

(8.185)

Literatura źródłowa:

302

---