1. Pobrano dwie próbki reprezentatywne n₁=20
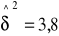
   ; n₂=8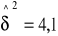
   . Przy założeniu normalności rozkładów zweryfikowana poziomie istotności α=0,05 hipotezę, że obydwie wariancje są równe wobec hipotezy alternatywnej H₁: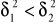
   . Zaproponować doświadczenie, w którym można wykorzystać powyższy test.

2. Z populacji, w której badana cecha ma rozkład normalny N(μ,δ) wykorzystano próbkę złożoną z 9 obserwacji. Na poziomie istotności α=0,05 zweryfikować hipotezę
   H₀: μ=2 przy alternatywie H₁: μ<2, jeśli średnia z próbek wynosi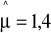
   . Zaproponować doświadczenie, w którym można wykorzystać powyższy test.

Odchylenie standardowe=4

3. Cecha podlega rozkładowi normalnemu N(μ,δ). Wiadomo, że δ²<3. Na poziomie istotności α=0,01 zweryfikować hipotezę H₀: δ²=3 wobec hipotezy alternatywnej
   H₁: δ²>3, jeśli pobrano próbę100 elementową i uzyskano estymator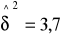
   . Zaproponować doświadczenie, w którym można wykorzystać powyższy test.

---