Kilka faktów z historii rachunku prawdopodobieństwa

1. Rachunek prawdopodobieństwa zaczął się kształtować w XVI wieku gdy zaczęto zauważać pewne prawidłowości w grach hazardowych. Pierwszy dostrzegł je i próbował opisać matematyk włoski Geronimo Cardano (1501-1576).

2. Poważniejszy rozwój rachunku prawdopodobieństwa nastąpił w wieku XVII dzięki pracom P. de Fermat'a i B. Pascal'a (matematycy francuscy).

3. Za twórcę rachunku prawdopodobieństwa jako działu matematyki uważamy szwajcarskiego matematyka Jakuba Bernoullie'go, który opracował te zagadnienia w wieku XVII.

4. Duży wkład i szybki rozwój tej nauki nastąpił w XIX wieku dzięki pracom Gaussa, Laplace'a, Pisson'a, Czybyszewa.

5. Pełnego opracowania i sformalizowania doczekał się rachunek prawdopodobieństwa dopiero w wieku XX dzięki pracom A. Kołogomorowa, matematyka rosyjskiego.

6. Rachunek prawdopodobieństwa stał się podstawą nowoczesnej fizyki - fizyki kwantowej opisującej zachowanie się mikrocząstek. Fizycy kwantowi wykazali, że w świecie mikrocząstek obowiązują prawa probabilistyczne czyli oparte na rachunku prawdopodobieństwa.

Zdarzenia losowe

Każde działanie, którego wyniku nie można z góry przewidzieć, nazywamy doświadczeniem losowym. Każdy możliwy wynik doświadczenia losowego nazywamy zdarzeniem elementarnym. Zbiór wszystkich takich zdarzeń nazywamy przestrzenią zdarzeń elementarnych.

Rozważając pewne zdarzenia losowe będziemy określać zbiór zdarzeń elementarnych oznaczanych literką Ω (omega). Są to wszystkie możliwe zdarzenia, które mogą zajść w pewnym doświadczeniu losowym np.:

rzut kostką.

Ω={1,2,3,4,5,6}

rzut trzykrotnie monetą:

Ω={(O,O,O);(O,O,R);(O,R,O);(R,O,O);(R,R,R);(R,R,O);(R,O,R);(O,O,R)}

losujemy dwie karty z talii 24 kart:

Ω={(9
,9
)...(9
,A
)...(A
,A
)}

W matematyce najczęściej każdy obiekt numerujemy co pozwala na wyłączne posługiwanie się liczbami, np. w ostatnim przypadku możemy postąpić następująco:

Karty=

Wszystkich możliwych par jest bardzo dużo. Zbiór zdarzeń elementarnych można jednak opisać posługując się "domyślnymi" wielokropkami:

Ω={(1,2)(1,3)(1,4)....(1,24)(2,1)(2,3)(2,4)....(2,24)....(24,1)(24,2)....(24,23)}

W celu określenia Ω zdarzenia można wypisać i przeliczyć, wypisać z wielokropkami i domyślnie przeliczyć, zastosować pewne zasady lub wzory do przeliczenia ilości zdarzeń.

n(Ω) - ilość wszystkich zdarzeń elementarnych.

Dla powyższych przykładów mamy:

n(Ω₁)=6

n(Ω₂)=8

n(Ω₃)=24⋅23=552

Dowolne podzbiory przestrzeni zdarzeń elementarnych nazywamy zdarzeniami losowymi. Wśród zdarzeń elementarnych danego doświadczenia losowego interesowały nas będą niektóre zdarzenia. Będziemy je nazywali zdarzeniami sprzyjającymi, np. losując 6 liczb w totolotku interesowała nas będzie jakaś wygrana, a więc zdarzenie polegające na tym, aby wśród sześciu wylosowanych liczb były przynajmniej trzy nasze.

Zdarzenia sprzyjające oznaczamy dużymi literami z początku alfabetu np.:

-wypadła szóstka (zdarzenie losowe)

A={6}

-trzy razy moneta upadła tą samą stroną (zdarzenie losowe)

B={(O,O,O);(R,R,R)}

-wylosowane karty tworzą parę (zdarzenie losowe)

C={(9
,9
)...(9
,9
)...(A
,A
)}

Rozwiązując zadania będziemy musieli przeliczać ilość zdarzeń sprzyjających zajściu danego zdarzenia. W zadaniach wymienionych wyżej będą to następujące ilości:

n(A)=1

n(B)=2

n(C)=6⋅3=18

Jeżeli wszystkie zdarzenia elementarne są jednakowo prawdopodobne, to możemy określić szansę zajścia danego zdarzenia losowego jako stosunek dwóch liczb: liczby zdarzeń elementarnych sprzyjających zajściu tego zdarzenia do liczby wszystkich zdarzeń elementarnych. Tak otrzymaną liczbę nazywamy prawdopodobieństwem zdarzenia.

Klasyczna definicja prawdopodobieństwa

Jeżeli wszystkie zdarzenia elementarne są jednakowo prawdopodobne, to prawdopodobieństwem zdarzenia losowego nazywamy iloraz

P(A)=

P(A) - prawdopodobieństwo zajścia zdarzenia A

n(A) - ilość zdarzeń sprzyjających

n(Ω) - ilość zdarzeń elementarnych

W naszych przykładach otrzymaliśmy następujące prawdopodobieństwa

P(A) =

P(B) =

P(C)=

Uwaga:

W większości podręczników i na wykładach rachunku prawdopodobieństwa wprowadza się zformalizowany zapis zbiorów zdarzeń. W naszych trzech przykładach zapisy takie wyglądałby następująco:

Ω₁={ω: ω={r} ; r∈{1,2,....,6} }

Ω₂={ω: ω=(m₁,m₂,m₃) ; m_i∈{O,R} ; i=1,2,3}

Ω₃={ω: ω=(k₁,k₂) ; k₁∈{1,....,24} ; k₂∈{1,....,24} ; k₁≠k₂ }

Zad.1.

Rzucamy 2-krotnie kostką. Jakie jest prawdopodobieństwo, że suma oczek będzie większa bądź równa 10?

Ω={(1,1);(1,2);(1,3);(1,4);(1,5);(1,6)
(2,1);(2,2);(2,3);(2,4);(2,5);(2,6)
(3,1);(3,2);(3,3);(3,4);(3,5);(3,6)
(4,1);(4,2);(4,3);(4,4);(4,5);(4,6)
(5,1);(5,2);(5,3);(5,4);(5,5);(5,6)
(6,1);(6,2);(6,3);(6,4);(6,5);(6,6)}

n(Ω)=36

A={(4,6);(5,5);(5,6);(6,6);(6,5);(6,4)}

n(A)=6
P(A)=

Zad.2.

Ze zbioru cyfr Z losujemy 3 cyfry bez zwracania. Jakie jest prawdopodobieństwo ułożenia z nich (układamy je w kolejności losowania) liczby podzielnej przez 3?

Z ={1,2,3,4}

Ω={(1,2,3),(1,2,4) ,(1,3,2),(1,3,4),(1,4,2),(1,4,3),

(2,1,3),(2,1,4),(2,3,1),(2,3,4),(2,4,1),(2,4,3),
(3,1,2),(3,1,4),(3,2,1),(3,2,4),(3,4,1),(3,4,2),
(4,1,2),(4,1,3),(4,2,1),(4,2,3),(4,3,1),(4,3,2)}

n(Ω)=24
A={(123),(132),(213),(231),(234),(243),(312),(321),(324),(342),(423),(432)}
n(A)=12

P(A)=

Matematyczny sposób opisu zbioru zdarzeń.

Opis zdarzeń z poprzedniego zadania (Zad. nr 2):

Ω = {ω: ω=(c₁,c₂,c₃); c_i∈{1,2,3,4}; i≠j⇒c_i≠c_j}

Zbiór Ω składa się z elementów ω,

po dwukropku następuje opis elementów.

ω jest ciągiem 3 elementowym.

Elementy ciągu należą do zbioru.

Jeśli wskaźniki są różne to i elementy są różne.

Elementy nie mogą się powtarzać.

Przeliczanie zbiorów zdarzeń

W zbiorach opisujących zdarzenia mamy do czynienia z ciągami (kolejność ważna) lub podzbiorami (kolejność dowolna).

a) ciągi zapisujemy w nawiasach okrągłych

ω =(a₁,a₂,a₃,...,a_n)

b) podzbiory będziemy oznaczali nawiasem klamrowym

ω ={z₁,z₂,z₃,...,z_n}

W podzbiorach elementy nie będą się powtarzać, a kolejność ich wymieniania jest bez znaczenia.

Zad. 3.

W urnie znajdują się 3 kule białe {1,2,3} oraz 2 czarne {4,5}. Losujemy z urny 2 kule. Oblicz prawdopodobieństwo, że będą jednokolorowe.

Rozwiązanie (I sposób)

Z={1,2,3,4,5}

Ω={{1,2}{1,3}{1,4}{1,5}
{2,3}{2,4}{2,5}
{3,4}{3,5}
{4,5}}

n(Ω)=10
n(A)=4

P(A)=

Rozwiązanie (II sposób)

n(Ω)=5⋅4=20
A={(1,2);(2,1);(1,3);(3,1);(2,3);(3,2);(4,5);(5,4)}
n(A)=8
P(A)=

Przykładowe zadanie maturalne z rachunku prawdopodobieństwa.

Powyższa elementarna wiedza z rachunku prawdopodobieństwa, pozwala już na rozwiązanie nawet części zadań z poziomu maturalnego.

Zadanie 4.

Ze zbioru liczb całkowitych spełniających nierówność x²-8x ≤ 0

a)

obliczyć prawdopodobieństwo wylosowania dwóch liczb, których suma wynosi 8,

b)

obliczyć prawdopodobieństwo wylosowania dwóch liczb pierwszych,

Rozwiązania.

x²-8x ≤0

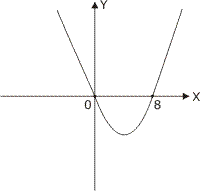
Z={x : x∈R; x²-8x≤0; x∈C}
x²-8x≤0
x²-8x=0
Δ=b²-4ac
Δ=64

=8
x₁=

x₂=



x∈<0,8>

a)

Wypisujemy zbiór zdarzeń elementarnych. Zdarzenia sprzyjające podkreślimy.

Z={0,1,2,3,4,5,6,7,8}

Ω={(0,1)(0,2)(0,3)(0,4)(0,5)(0,6)(0,7)(0,8)
(1,2)(1,3)(1,4)(1,5)(1,6)(1,7)(1,8)(1,0)
(2,0)(2,1)(2,3)(2,4)(2,5)(2,6)(2,7)(2,8)
(3,0)(3,1)(3,2)(3,4)(3,5)(3,6)(3,7)(3,8)
(4,0)(4,1)(4,2)(4,3)(4,5)(4,6)(4,7)(4,8)
(5,0)(5,1)(5,2)(5,3)(5,4)(5,6)(5,7)(5,8)
(6,0)(6,1)(6,2)(6,3)(6,4)(6,5)(6,7)(6,8)
(7,0)(7,1)(7,2)(7,3)(7,4)(7,5)(7,6)(7,8)}

n(Ω)=8⋅9=72
n(A)=8
l₁+l₂=8

P(A)=

b)

Z={2,3,5,7} -liczby pierwsze

Wypisujemy zbiór zdarzeń sprzyjających:

A={(2,3)(2,5)(2,7)
(3,2)(3,5)(3,7)
(5,2)(5,3)(5,7)
(7,2)(7,3)(7,5)}

n(A)=12
n(Ω)=72
P(A)=

Ćwiczenie 1

Rozwiąż zadania 1- 6 str. 60-61, 15-17 - str. 63 - 64 z podręcznika.

---