POLITECHNIKA CZĘSTOCHOWSKA

LABORATORIUM FIZYKI

Ćwiczenie nr 4.

Temat:

Pomiar szerokości przerwy energetycznej w półprzewodnikach

Skład grupy:

Frydrych Dariusz

Łakomy Paweł

Wydz. Elektryczny

Gr. II Sem. IV

WSTĘP

Zgodnie z hipotezą de Brogle'a każdej mikro cząsteczce przypisuje się falę materii . Falę stowarzyszoną z cząsteczką opisuje równanie Schrodingera .

-Rozwiązania

te istnieją jeżeli n, l, m_l są równe pewnym liczbom całkowitym , które to nazywamy liczbami kwantowymi .

n - główna liczba kwantowa

l - orbitalna liczba kwantowa

m - magnetyczna liczba kwantowa

Dla atomów wieloelektronowych obowiązuje zasada zwana Zakazem Pauliego - która mówi ,że w danym atomie żadne dwa elektrony nie mogą mieć tego samego zespołu liczb kwantowych. Dzięki temu można ustalić konfigurację elektronową danego atomu.

Tworzenie się pasm w ciałach stałych:

Gdy odległość między atomami stopniowo maleje zewnętrzne elektrony dwóch atomów zaczynają oddziaływać ze sobą ,powodując rozszczepienie pojedynczego poziomu energetycznego na dwa podpoziomy. Zbliżenie atomów powoduje obniżenie barier potencjalnych i zmniejszenie ich szerokości. Dlatego elektrony 3s mają możliwość swobodnego poruszania się od jednego atomu do drugiego.W krysztale złożonym z N atomów, każdy pojedynczy poziom energetyczny w izolowanym atomie rozszczepia się na N bardzo blisko siebie leżące podpoziomy tworząc pasmo. Szerokość pasma zależy głównie od odległości międzyatomowych w krysztale. Pasmo odpowiadające pierwszemu stanowi wzbudzenia w atomie kryształu nazywa się pasmem przewodnictwa , które w danej chwili może być puste , lub obsadzone. Pomiędzy pasmem przewodnictwa a walencyjnym jest pasmo wzbronione inaczej przerwa energetyczna, której szerokość Eg jest różna dla różnych kryształów. Zewnętrzne pole elektryczne przyłożone do kryształu może tylko wpłynąć na ruch elektronów w paśmie niewypełnionym całkowicie . W paśmie wypełnionym całkowicie nie ma wolnych poziomów i elektron nie może zmieniać swojego ruchu. Przyjmuje się ,że kryształ jest półprzewodnikiem jeżeli Eg < 3eV po wyżej tej granicy mamy do czynienia z dielektrykami.

Statystyka Maxwella-Boltzmana i Fermiego Diraca.

Układ jako całość nie zależy od zachowania się poszczególnych cząstek ,a jego zachowanie podlega prawom statystycznym. Znając funkcję rozkładu energii można za jej pomocą obliczyć średnią wartość energii ,natomiast z funkcji rozkładu prędkości znajdujemy prędkość średnią. Funkcja rozkładu dla elektronów i innych cząsteczek o spinie połówkowym podana przez Fermiego Diraca ma postać:

E_f - energia Fermiego

Cząsteczki podlegające temu rozkładowi nazywamy fermionami. Dla T=0K i temperatur wyższych gdy E>E_f f(E)=1oznacza to ,że poziomy położone powyżej pewnego poziomu zwanego poziomem Fermiego w temp.0K nie są zajęte przez elektrony (prawdopodobieństwo obsadzeń=0) natomiast poziomy położone poniżej poziomu Fermiego są całkowicie zajęte (prawdopodobieństwo obsadzeń=1) Poziom Fermiego jest to więc najwyższy poziom zajęty przez elektrony w metalu w temp. 0K, a energia Fermiego jest max. energią jaka może mieć elektron w metalu w temp. 0K.

Zachowanie zwykłego gazu dla którego nie obowiązuje Zakaz Pauliego opisuje funkcja rozkładu Boltzmanna:

- potencjał chemiczny

f(E) ma max. dla E=0 i zbliża się asymptotycznie do zera ,dla E największe prawdopodobieństwo zapełnienia posiadają stany o niskich energiach w miarę wzrostu temp. prawdopodobieństwo obsadzenia stanów maleje.

W wysokich temp. funkcja F-D przechodzi w funkcję M-B. Z funkcji M-B można znaleźć średnią energię cząstki prędkość średnią kwadratową. Cząstki opisane statystyką F-D - fermiony nazywamy gazem zwyrodniałym (zdegenerowanym) w odróżnieniu od cząstek opisanych statystyką M-B zwanych gazem niezwyrodniałym

Zależność oporu półprzewodników od temperatury. Zasada pomiaru

przerwy energetycznej.

Temperaturowa zależność przewodnictwa elektrycznego półprzewodników jest ściśle związana z zależnością ruchliwości i koncentracji nośników od temperatury.

Półprzewodnikami charakteryzującymi się silną zależnością oporu od temp. są termistory.

lub

Zależność temperaturową oporu termistora charakteryzuje temperaturowy współczynnik

gdzie

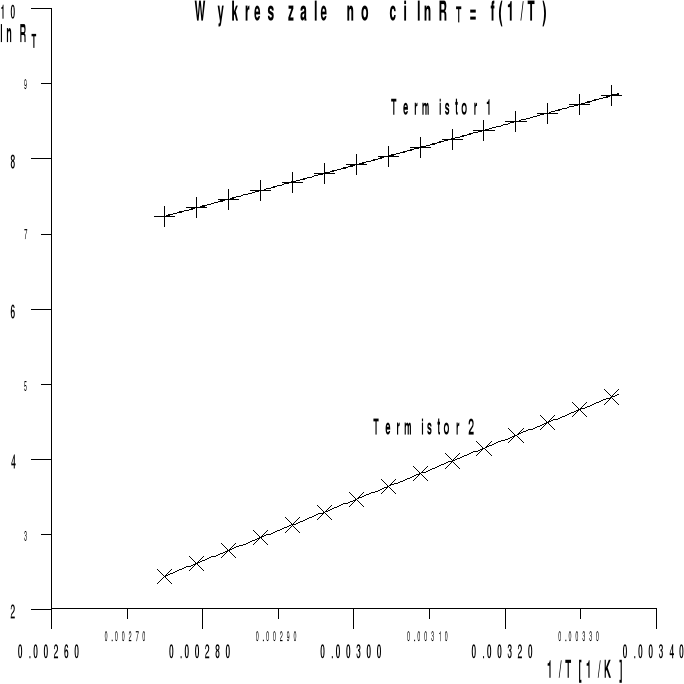
Badając zależność oporu od temp. obliczamy Eg jako współczynnik kierunkowy prostej lnR(1/T).

Przebieg ćwiczenia.

Schemat połączeń.

Tabele wyników:

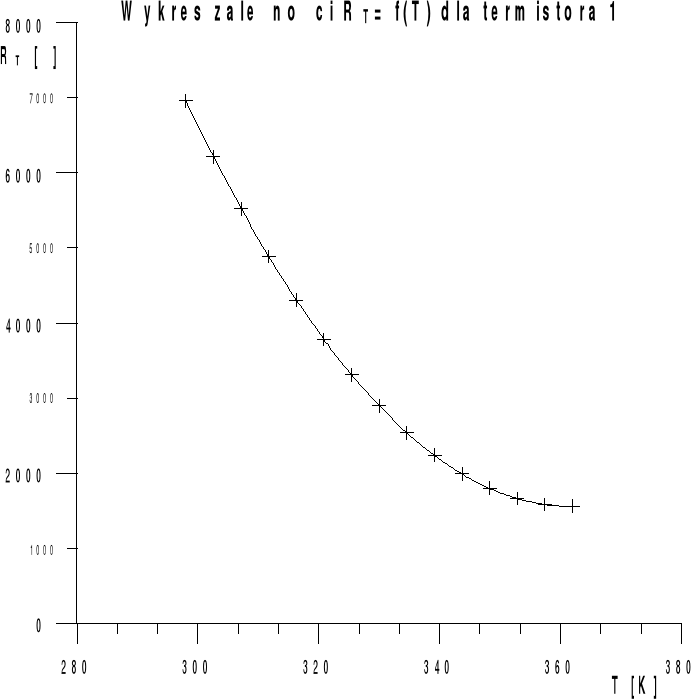
Dla termistora 1

t	I	u	RT	lnRT	T	1/T	Eg	B	T^2	αT
[^oC]	[A]	[V]	[Ω]	[-]	[K]	[K^-1]	[eV]	[K]	[K^2]	[K^-1]
25 30 35 40 45 50 55 60 65 70 75 80 85 90	1,2 1,4 1,6 1,9 2,2 2,45 2,85 3,15 3,5 4 4,5 5 5,6 6,15	8.6 8.6 8.6 8.6 8.6 8.6 8.6 8.6 8.6 8.6 8.6 8.6 8.6 8.6	7166,67 6142,86 5375 4526,32 3909,09 3510,2 3017,54 2730,16 2457,14 2150 1911,11 1720 1535,71 1398,37	8,88 8,72 8,59 8,42 8,27 8,16 8,01 7,91 7,81 7,67 7,56 7,45 7,34 7,24	298 303 308 313 318 323 328 333 338 343 348 353 358 363	0.00335 0.0033 0.00324 0.00319 0.00314 0.00309 0.00304 0.003 0.00295 0.00291 0.00287 0.00283 0.00279 0.00275	0.4686 0.4686 0,4686 0,4686 0,4686 0,4686 0,4686 0,4686 0,4686 0,4686 0,4686 0,4686 0.4686 0.4686	2719.55 2719.55 2719.55 2719.55 2719.55 2719.55 2719.55 2719.55 2719.55 2719.55 2719.55 2719.55 2719.55 2719.55	88804 91809 94864 97969 101124 104329 107584 110889 114244 117649 121104 124609 128164 131769	-0.03062 -0.02962 -0.02867 -0.02776 -0.02689 -0.02607 -0.02528 -0.02452 -0.02381 -0.02312 -0.02246 -0.02182 -0.02122 -0.02064

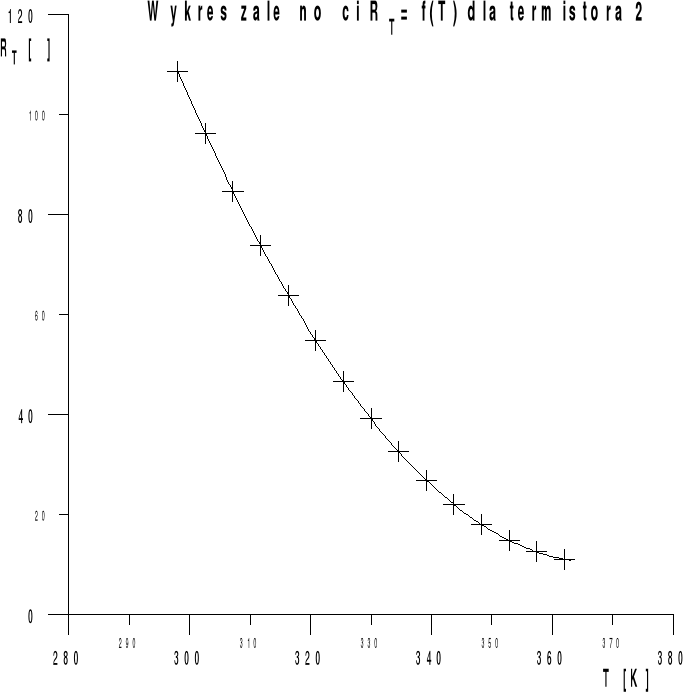
Dla termistora 2.

t	I	U	RT	lnRT	T	1/T	Eg	B		T^2	αT
[^oC]	[A]	[V]	[Ω]	[-]	[K]	[K^-1]	[eV]	[K]	[K^2]		[K^-1]
90 85 80 75 70 65 60 55 50 45 40 35 30 25	260 187 147 120 100 80 65 51 45 40 32 30 25 20	2.3 2.3 2.3 2.3 2.3 2.3 2.3 2.3 2.3 2.3 2.3 2.3 2.3 2.3	8.85 12.30 15.65 19.17 23 28.75 35.38 45.10 51.11 57.50 71.88 76.67 92 115	2.18 2.51 2.75 2.95 3.14 3.36 3.57 3.81 3.93 4.05 4.27 4.34 4.52 4.74	363 358 353 348 343 338 333 328 323 318 313 308 303 298	0.00275 0.00279 0.00283 0.00287 0.00291 0.00295 0.003 0.00304 0.00309 0.00314 0.00319 0.00324 0.0033 0.00335	0,7233 0,7233 0,7233 0,7233 0,7233 0,7233 0,7233 0,7233 0,7233 0,7233 0,7233 0,7233 0,7233 0,7233	4196.724196,724196,724196,724196,724196,724196,724196,724196,724196,724196,724196,724196,724196,72		131769 128164 124609 121104 117649 114244 110889 107584 104329 101124 97969 94864 91809 88804	-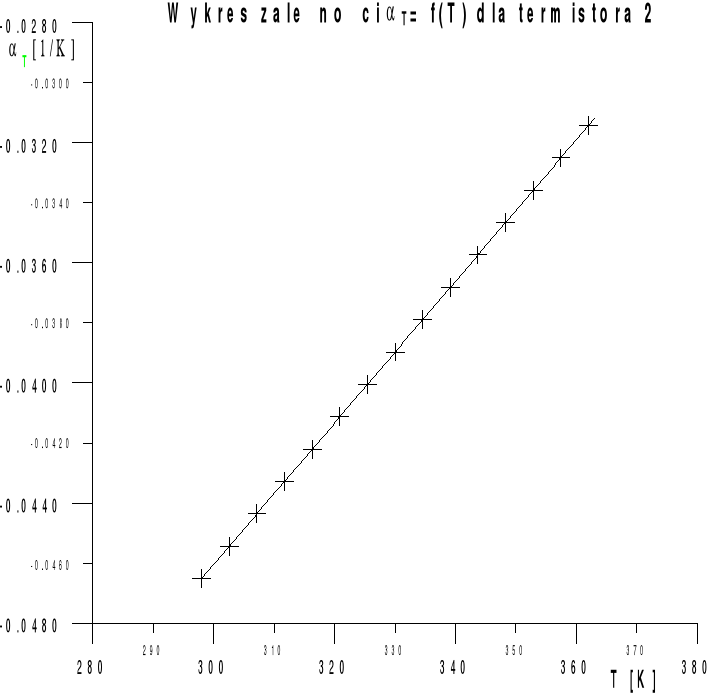0.03185 -0.03274 -0.03368 -0.03465 -0.03567 -0.03673 -0.0785 -0.03901 -0.04023 -0.04150 -0.04284 -0.04424 -0.04571 -0.04726

Przykładowe obliczenia:

Rezystancja termistora: [Ω]

dla termistora 1 R_T1 = 8,6/1,2⋅ 10^-3 = 7166,67 [Ω]

dla termistora 2 R_T2 = 2,3/260⋅ 10^-3 = 8.85 [Ω]

Stała materiałowa B: [K]

dla termistora 1 B = (8,88 - 7,24) / (0.00335 - 0,00275 ) = 2719.55 [K]

dla termistora 2 B = (4,74 - 2,18) / (0,00335 - 0,00275) = 4196,72 [K]

Szerokość przerwy energetycznej: [eV]

gdzie k =1.3806⋅10^-23 [J/K] - stała Boltzmana

eV więc k = 0.86169555⋅10^-4 [eV/K]

dla termistora 1: E_g1 = 2719,55 ⋅ 2⋅ 0,8616955 ⋅ 10^-4 = 0,4686 [eV]

dla termistora 2: E_g1 = 4196,72 ⋅ 2⋅ 0,8616955 ⋅ 10^-4 = 0,7233 [eV]

Temperaturowy współczynnik oporu: [K^-1]

dla termistora 1: α_T1 = -2719,55/88804 = -0,3062 [K^-1]

dla termistora 2: α_T1 = -4196,72/131769 = -0,03185 [K¹]

Obliczenia

gdzie - opór termistora w temperaturze nieskończenie wysokiej

_- opór termistora w temperaturze 25^oC

dla termistora 1: R_∞ = 7166,67 ⋅ exp(2719,55/298) = 65870621[Ω]

dla termistora 2: R_∞ = 115 ⋅ exp(4196,72/298) = 1,50261 ⋅ 10⁸ [Ω]

Tabela błędów

R1	B1	Eg		R2	B2	Eg
[]	[]	[eV]	[]	[]	[]	[eV]	[]
483,33 361,54 272,65 219,36 170,02 140.48 118,63 99,97 85,33 67,23 58,36 52,63 42,68 37,23	82,1212 82,1212 82.1212 82.1212 82.1212 82.1212 82.1212 82.1212 82.1212 82.1212 82.1212 82.1212 82.1212 82.1212	0.01415 0.01415 0.01415 0.01415 0.01415 0.01415 0.01415 0.01415 0.01415 0.01415 0.01415 0.01415 0.01415 0.01415	0.000873 0.000862 0.000842 0.000823 0.000812 0.000803 0.000784 0.000758 0.000729 0.000711 0.000684 0.000666 0.000639 0.000619	0.5846 0.59215 0.72562 0.87085 1.12635 1.32918 1.68953 1.86356 2.31264 2.89633 3.43666 4.55555 5.23456 6.56333	181.3256 181,3256 181,3256 181.3256 181.3256 181.3256 181.3256 181.3256 181.3256 181.3256 181.3256 181.3256 181.3256 181.3256	0.03125 0.03125 0.03125 0.03125 0.03125 0.03125 0.03125 0.03125 0.03125 0.03125 0.03125 0.03125 0.03125 0.03125	0.00133 0.00135 0.00138 0.00141 0.00147 0.00149 0.00152 0.00156 0.00160 0.00163 0.00168 0.00174 0.00812 0.00883

Przykładowe obliczenia błędów metodą różniczki zupełnej

Błąd popełniony przy wyznaczaniu ⇒

gdzie: ΔU, ΔI - błędy bezwzględne mierników

[V]

[A] [A]

dla termistora 1: ΔR_T1 = (0,15/0,0012) + (8,6⋅ 6⋅10^-5/(0,0012)² = 483,33 [Ω]

dla termistora 2: ΔR_T1 = (0,15/0,26) + (2,3⋅ 6⋅10^-5/(0,26)² = 0,5846 [Ω]

Błąd popełniony przy wyznaczaniu ⇒

gdzie:ΔT=1[K]

Błąd popełniony przy wyznaczaniu ⇒

dla term.1: ΔE_g1 = 2⋅0,8616955⋅ 10^-4 ⋅ 82,1212 = 0,01415 [eV]

dla term.2: ΔE_g1 = 2⋅0,8616955⋅ 10^-4 ⋅ 181,3256 = 0,03125 [eV]

Błąd popełniony przy wyznaczaniu α_T

⇒ 1

dla termistora 1: Δα_T1 = (82,1212/88804) + (2719,55/(-2⋅298³)) = 0,000873 [K^-1]

dla termistora 2: Δα_T1 = (181,3256/131769) + (4196,72/(-2⋅363³)) = 0,00133 [K^-1]

WNIOSKI:

Przeprowadzone ćwiczenie pozwoliło nam na obserwację wpływu temperatury na półprzewodniki. Jak wynika z pomiarów, w miarę wzrostu temperatury wzrasta przewodnictwo w tego rodzaju materiałach. Jest to możliwe dzięki wzbudzeniu termicznemu. Przerwa energetyczna maleje czyli przewodnictwo elektryczne wzrasta. Dzieje się tak gdyż elektrony przechodzą z pasma walencyjnego do pasma przewodnictwa gdzie mogą się swobodnie poruszać i brać udział w przewodzeniu prądu. W przewodnictwie tym biorą udział zarówno elektrony w paśmie przewodnictwa, jak i dziury w paśmie walencyjnym .

Wpływ temperatury na półprzewodniki ilustrują także znakomicie załączone wykresy. Widzimy, że w miarę wzrostu temperatury maleje opór półprzewodnika, wzrasta tym samym prąd płynący przez ten element. Wzrasta także temperaturowy współczynnik oporu obu termistorów.

Na błędy w ćwiczeniu wpływ miała niedokładność odczytu z przyrządów pomiarowych. Błąd także wprowadzał termometr o najmniejszej podziałce 1^oC. Błędy te są jednak nieznaczne.

---