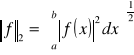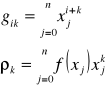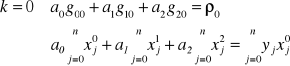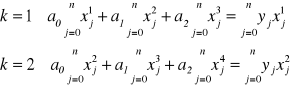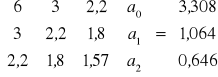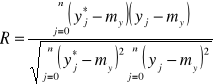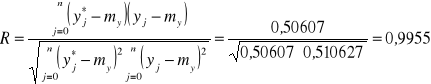APROKSYMACJA

Zagadnienie interpolacji (poznane wcześniej) polega na poszukiwaniu pewnej funkcji interpolującej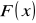
, która na danym, dyskretnym zbiorze argumentów pokrywa się z wartościami funkcji interpolowanej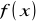
. Takie postępowanie jest często niedogodne. Przy interpolacji wielomianowej duża liczba węzłów interpolacji wymaga skonstruowania wielomianu interpolacyjnego wysokiego stopnia. Ponadto często mamy do czynienia z funkcją, której wartości na dyskretnym zbiorze argumentów są określone empirycznie (są np.: wynikami pomiarów), a więc mogą być obarczone błędami i wówczas żądanie dokładnego przyjmowania przez szukaną funkcję niedokładnych danych wartości nie ma sensu.

Zajmiemy się teraz zagadnieniem bardziej ogólnym, w którym warunek, aby funkcja dana i funkcja szukana przyjmowały dokładnie te same wartości na zbiorze danych z góry punktów węzłowych, nie musi być spełniony.

Funkcję
, znaną lub określoną tablicą wartości, będziemy aproksymować (zastępować) inną funkcją
, zwaną funkcją aproksymującą lub przybliżeniem funkcji
. Przybliżenie takie powoduje pojawienie się błędów, zwanych błędami aproksymacji (przybliżenia) i problem oszacowania tych błędów oraz ich wielkość mają istotny wpływ na wybór metody aproksymacyjnej.

Niech
będzie funkcją, którą chcemy aproksymować,
- pewną przestrzenią liniową unormowaną
, a
- m-wymiarową podprzestrzenią liniową przestrzeni
.

Aproksymacja funkcji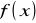
polega na wyznaczeniu takich współczynników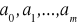
funkcji

gdzie:
są funkcjami bazowymi
wymiarowej podprzestrzeni liniowej
, aby funkcja
spełniała pewne warunki, np.: minimalizowała normę różnicy

Aproksymacja podana powyżej nosi nazwę aproksymacji liniowej.

Funkcje bazowe.

Jeżeli funkcja aproksymowana
jest funkcją ciągłą na przedziale
(jest elementem nieskończenie wymiarowej przestrzeni liniowej
), to funkcje
będą elementami pewnej
wymiarowej podprzestrzeni
.

Jedną z często obieranych podprzestrzeni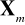
jest podprzestrzeń funkcji trygonometrycznych z bazą:

1, sinx, cosx, sin2x, cos2x,…, sinkx, coskx

szczególnie przydatna, gdy aproksymowana funkcja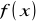
jest funkcją okresową.

Inną, często obieraną podprzestrzenią, jest podprzestrzeń wielomianów stopnia co najwyżej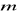
z bazą jednomianów

1, x, x², x³,…, x^m

Współczynniki liczbowe.

Zagadnienie najlepszej aproksymacji przy wybranych funkcjach bazowych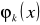
sprowadza się do znalezienia wartości współczynników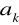
takich aby otrzymać minimum wyrażenia

i aby istniało jedyne możliwe rozwiązanie tego zagadnienia ze względu na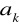
.

Normą tutaj może być np.:

Norma Czebyszewa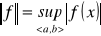

Norma L₂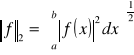

Będziemy rozważać dwa rodzaje aproksymacji:

Aproksymacja średniokwadratowa.

Dla funkcji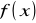
określonej na przedziale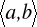
poszukujemy minimum całki

a dla funkcji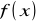
danej na dyskretnym zbiorze argumentów poszukujemy minimum sumy (metoda najmniejszych kwadratów)

dla

gdzie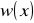
ustalona z góry funkcja wagowa. Będziemy przyjmować, że jest równa jedności. W pewnych specjalnych przypadkach dobiera się inne funkcje wagowe np.: jeżeli chcemy, aby otrzymane przybliżenie było w pewnych punktach lepsze (bowiem wiemy, że w tych punktach wartości funkcji znamy z mniejszym błędem), to przyjmujemy w tych punktach większe wartości funkcji wagowej.

Aproksymacja jednostajna

Dla funkcji
określonej na przedziale
poszukujemy funkcji
dającej najmniejsze maksimum różnicy między
a
na całym przedziale

Aproksymacja średniokwadratowa (dla dyskretnych wartości)

Niech będzie dana funkcja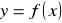
, która na pewnym zbiorze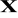
punktów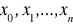
przyjmuje wartości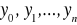
. Wartości te możemy znać tylko w przybliżeniu, z pewnymi błędami (np. jako wyniki pomiarów obarczonych błędami obserwacji), przy czym błędy te mogą być niejednokrotnie dosyć duże, co w istotny sposób wpływa na jakość aproksymacji. Będziemy poszukiwać takiej funkcji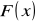
przybliżającej daną funkcję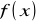
, która umożliwi wygładzenie funkcji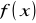
, tzn. pozwoli z zakłóconych błędami danych wartości funkcji przybliżanej otrzymać gładką funkcję przybliżającą, z dużym prawdopodobieństwem mało odchylającą się od funkcji przybliżanej zarówno między węzłami, jak i w węzłach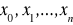
, jeżeli tylko przyjmiemy, że funkcja przybliżana ma dość gładki przebieg.

Niech
,
będzie układem funkcji bazowych podprzestrzeni
. Poszukujemy wielomianu uogólnionego
, będącego najlepszym przybliżeniem średniokwadratowym funkcji
na zbiorze
, tj. funkcji w postaci

.

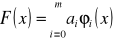
Po podstawieniu do wzoru na aproksymację średniokwadratową otrzymamy:

Aby znaleźć współczynniki
obliczamy pochodne cząstkowe funkcji
względem zmiennych
. Z warunku na poszukiwanie ekstremów funkcji wielu zmiennych otrzymamy:

otrzymamy wówczas układ
równań liniowych
niewiadomymi

zwany układem normalnym. Ponieważ funkcje
tworzą bazę przestrzeni
, więc układ ma wyznacznik różny od zera i rozwiązanie tego układu daje minimum funkcji
.

Aproksymacja wielomianowa

Jeżeli jako funkcje bazowe przyjmiemy ciąg jednomianów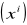
,
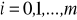
to otrzymamy

Zmieniając kolejność sumowania, mamy:

oznaczając

otrzymamy układ normalny w postaci

Można wykazać, że jeżeli punkty
są różne i
to wyznacznik układu jest różny od zera, a więc układ ten ma jednoznaczne rozwiązanie. Jeżeli
to wielomian aproksymacyjny
pokrywa się z wielomianem interpolacyjnym dla punktów
i wówczas
. W praktyce stopień wielomianu jest, i powinien być, znacznie mniejszy od liczby punktów

wtedy bowiem korzystamy z dużej ilości informacji (np.: wyników pomiarów) uzyskując równocześnie prostsze (niskiego stopnia) funkcje aproksymujące.

Wielomian aproksymujący daną funkcję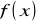
w sensie najmniejszych kwadratów powinien mieć stopień na tyle wysoki, aby dostatecznie przybliżać aproksymowaną funkcję, a jednocześnie stopień ten powinien być wystarczająco niski, aby wielomian ten wygładzał losowe błędy wynikające np.: z pomiarów.

Nie powinno się stosować wielomianów o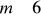
, ponieważ układ równań jest wtedy źle uwarunkowany, wskutek czego otrzymane wyniki obliczeń na maszynach cyfrowych mogą być tak bardzo złe, iż nie nadają się do praktycznego wykorzystania przy aproksymacji.

Przykład

Funkcja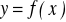
jest określona przez następujące dyskretne wartości

x	0	0,2	0,4	0,6	0,8	1
y	1,026	0,768	0,648	0,401	0,272	0,193

Znaleźć wielomian aproksymujący stopnia drugiego.

Mamy do rozwiązania układ normalny w postaci:

gdzie: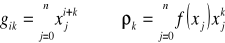

k - numer parametru liczbowego k=0,1,m=2

i - potęga x (xⁱ) i=0,1,m=2

j - liczba punktów j=0,1,…,n

Obliczenia najprościej zrobić w tablicy

		xj	yj	xj^2	xj^3	xj^4	xjyj	xj^2yj
		0	1.026	0	0	0	0	0
		0.2	0.768	0.04	0.008	0.0016	0.1536	0.03072
		0.4	0.648	0.16	0.064	0.0256	0.2592	0.10368
		0.6	0.401	0.36	0.216	0.1296	0.2406	0.14436
		0.8	0.272	0.64	0.512	0.4096	0.2176	0.17408
		1	0.193	1	1	1	0.193	0.193
suma	3	3.308	2.2	1.8	1.5664	1.064	0.64584

Stąd otrzymamy następujący układ równań do rozwiązania

Skąd

Stąd aproksymująca funkcja jest określona równaniem:

Oszacowanie jakości aproksymacji

Znajomość funkcji regresji nie umożliwia oceny rozbieżności między modelem matematycznym a danymi doświadczalnymi. Jako przykład można podać, że dla tej samej funkcji regresji punkty mogą leżeć blisko lub daleko od tej funkcji.

Dalej podamy sposób badania jakości aproksymacji przez współczynnik korelacji.

W tym celu wprowadźmy zbiór wartości funkcji
,
które będą oznaczać wartości zmiennej
obliczone ze wzoru aproksymującej funkcji
, natomiast
dalej oznaczają wyniki pomiarów.

Dla funkcji aproksymującej definiuje się współczynnik korelacji:

gdzie:

Wartość współczynnika korelacji zawiera się w przedziale [0,1] i im jest bliższy jedynki , tym silniejsza jest zależność między funkcją regresji a wynikami badań.

Przykład

Wyznaczyć współczynnik korelacji dla poprzedniego przykładu

Obliczenia najprościej wykonać w tablicy

xj	yj	yj^*	yj^*-my	yj-my	(yj^*-my)(yj-my)	(yj^*-my)^2	(yj-my)^2
0	1.026	1.0238929	0.47256	0.474667	0.224308254	0.223313	0.225308
0.2	0.768	0.7939643	0.242631	0.216667	0.05257004	0.05887	0.046944
0.4	0.648	0.5947143	0.043381	0.096667	0.004193492	0.001882	0.009344
0.6	0.401	0.4261429	-0.12519	-0.15033	0.018820302	0.015673	0.0226
0.8	0.272	0.28825	-0.26308	-0.27933	0.073487944	0.069213	0.078027
1	0.193	0.1810357	-0.3703	-0.35833	0.13268998	0.13712	0.128403
my=	0.551333			suma	0.506070012	0.50607	0.510627

5

---