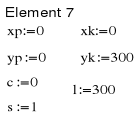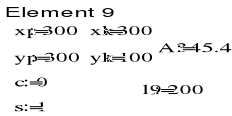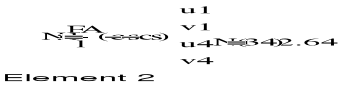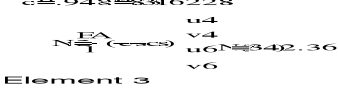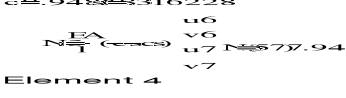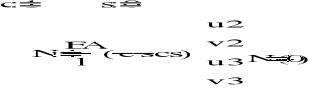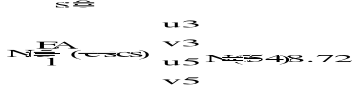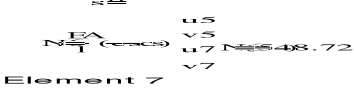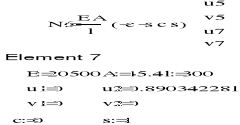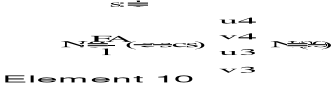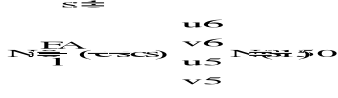PP2 WM2c, Agregacja macierzy sztywności układu

POLITECHNIKA WARSZAWSKA Wydział Inżynierii Lądowej

INSTYTUT MECHANIKI KONSTRUKCJI INŻYNIERSKICH Zakład Wytrzymałości Materiałów, Teorii Sprężystości i Plastyczności

Wytrzymałość Materiałów II
PRACA PROJEKTOWA nr 2
Temat:	Kratownica płaska - zagadnienie wyboczenia oraz metoda elementów skończonych
Imię i nazwisko:

Data wykonania: 22.05.2006 r.		Grupa dziekańska	3	Rodzaj studiów	Zaoczne
				Rok akademicki	2005/06	Semestr	IV

Prowadzący zajęcia: dr inż. Szczepan Lutomirski
Ocena:

0x01 graphic

2. WYMIAROWANIE PRĘTÓW KRATOWNICY

R= f_d = 205 MPa wytrzymałość obliczeniowa stali

R_e= R_eH= 230 MPa górna granica plastyczności stali

R_H = 190 MPa granica proporcjonalności stali

E = 2.05 Gpa moduł Younga stali

Dane:

Przekrój A1 - pas dolny (pręty 1, 2, 3) - Rozciągany siłą⁺N_max1 = 579,75 kN

Przekrój A2 - pas górny (pręty 4, 5, 6) - Ściskany siłą ^-N_max2 = 550,00 kN

Przekrój A3 - pozostałe pręty (7,8,9,10,11) -Rozciągane siłą ⁺N_max3 = 237,17 kN

Ściskane siłą ^-N_max3 = 459,62 kN

2.1. Przekrój A1 ] [

z założenia:

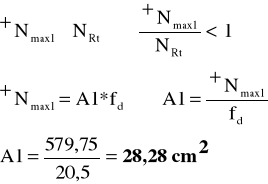
0x01 graphic

przyjęto przekrój 2 x ] 120

A1 = 2 * 17,0 = 34,00 cm²

Sprawdzenie nośności przekroju

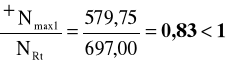
2) 0x01 graphic

2.2. Przekrój A2 ] [

μ = 1; ψ = 1; n = 1,6; l = 300 cm; ^-N_max2 = 550,00 kN

przyjęto:

A2 - 2 x ] 180 - A2 = 2*28,0 = 56,0 cm² e = 1,92 cm

Moment i promień bezwładności:

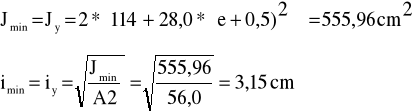
0x01 graphic

smukłość maksymalna:

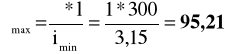
smukłość porównawcza:

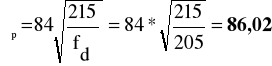
smukłość względna:

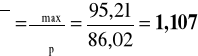
współczynnik wyboczeniowy:

Obliczeniowa siła krytyczna

Nośność obliczeniowa (sprawdzenie):

2.3. Przekrój A3 _┘└

μ = 1; ψ = 1; n = 1,6; l = 424 cm; ^-N_max3 = 459,62 kN (pręt 8)

przyjęto:

A3 - 2 x _┘ 100x100x12 - A2 = 2*22,7 = 45,4 cm² e = 2,90 cm

Moment i promień bezwładności:

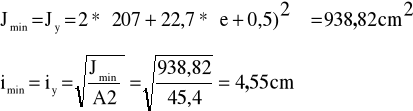
0x01 graphic

smukłość maksymalna:

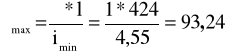
0x01 graphic

smukłość porównawcza:

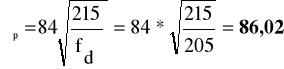
0x01 graphic

smukłość względna:

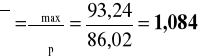
0x01 graphic

współczynnik wyboczeniowy:

Obliczeniowa siła krytyczna:

Sprawdzenie nośności:

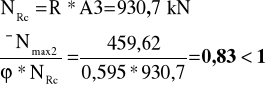
Zestawienie przekrojów:

przekrój	schemat		Pole przekroju	pręty	J_min
A1	] [	2x [ 120	34,0 cm²	1, 2, 3	236,34 cm⁴
A2	] [	2x [ 180	56,0 cm²	4, 5, 6	555,96 cm⁴
A3	_┘└	2x _└ 100x100x12	45,4 cm²	7, 8, 9, 10, 11	938,82 cm⁴

3. WYZNACZENIE PRZEMIESZCZENIA PIONOWEGO WĘZŁA K (6)

Siły w prętach kratownicy obciążonej siłą jednostkową w węźle K (6)

0x01 graphic

Obliczenie przemieszczenia pionowego węzła K (6)

Pręt	L (m)	EA [kN]	N [kN]	N¹ [ - ]
1	3,16	697000	342,58	0,53	0,000823175
2	3,16	697000	342,58	0,53	0,000823175
3	3,16	697000	579,75	2,11	0,005545970
4	3,00	1148000	0,00	0,00	0,000000000
5	3,00	1148000	-550,00	-2,00	0,002874564
6	3,00	1148000	-550,00	-2,00	0,002874564
7	3,00	930700	0,00	0,00	0,000000000
8	4,24	930700	-459,62	-0,71	0,001486666
9	2,00	930700	0,00	0,00	0,000000000
10	3,16	930700	237,17	1,58	0,001272314
11	1,00	930700	-150,00	0,00	0,000000000

			Przesunięcie Pionowe węzła K (6)		0,0157 m

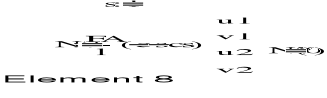
4. OBLICZENIE SZTYWNOŚCI ELEMENTÓW KRATOWNICY

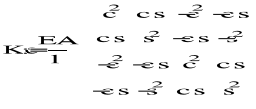
0x08 graphic

Agregacja macierzy sztywności układu

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1985 0 1098	662 0 1098	0	0	-1098	-1098	-1985	-662
2		221 3102 1098	0	-3102	-1098	-1098	-662	-221
3			3827 0	0 0	-3827	0
4				0 3102	0	0
5					3827 3827 1098 0 2651	0 0 1098 0 -884	0	0	-3827	0	-2651	884
6						0 0 1098 4654 295	0	-4654	0	0	884	-295
7							1985 1985 0	662 662 0			-1985	-662
8								221 221 4654			-662	-221
9									3827 3827 0	0 0 0	0	0	-3827	0
10										0 0 9307	0	-9307	0	0
11											1985 1985 2651 0	662 662 -884 0	-1985	-662
12												221 221 295 9307	-662	-221
13													1985 3827	662 0
14														221 0

Zagregowana macierz sztywności

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	3083	1760	0	0	-1098	-1098	-1985	-662	0	0	0	0	0	0
2		4421	0	-3102	-1098	-1098	-662	-221	0	0	0	0	0	0
3			3827	0	-3827	0	0	0	0	0	0	0	0	0
4				3102	0	0	0	0	0	0	0	0	0	0
5					11403	214	0	0	-3827	0	-2651	884	0	0
6						6047	0	-4654	0	0	884	-295	0	0
7							3970	1324	0	0	-1985	-662	0	0
8								5096	0	0	-662	-221	0	0
9									7654	0	0	0	-3827	0
10										9307	0	-9307	0	0
11											6621	440	-1985	-662
12												10044	-662	-221
13													5812	662
14														221

Modyfikacja macierzy sztywności przez wprowadzenie warunków brzegowych

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1	0	0	0	0	0	0	0	0	0	0	0	0	0
2		1	0	0	0	0	0	0	0	0	0	0	0	0
3			3827	0	-3827	0	0	0	0	0	0	0	0	0
4				3102	0	0	0	0	0	0	0	0	0	0
5					11403	214	0	0	-3827	0	-2651	884	0	0
6						6047	0	-4654	0	0	884	-295	0	0
7							3970	1324	0	0	-1985	-662	0	0
8								5096	0	0	-662	-221	0	0
9									7654	0	0	0	-3827	0
10										9307	0	-9307	0	0
11											6621	440	-1985	0
12												10044	-662	0
13													5812	0
14														1

Pełna macierz sztywności: K

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0	1	0	0	0	0	0	0	0	0	0	0	0	0
3	0	0	3827	0	-3827	0	0	0	0	0	0	0	0	0
4	0	0	0	3102	0	0	0	0	0	0	0	0	0	0
5	0	0	-3827	0	11403	214	0	0	-3827	0	-2651	884	0	0
6	0	0	0	0	214	6047	0	-4654	0	0	884	-295	0	0
7	0	0	0	0	0	0	3970	1324	0	0	-1985	-662	0	0
8	0	0	0	0	0	-4654	1324	5096	0	0	-662	-221	0	0
9	0	0	0	0	-3827	0	0	0	7654	0	0	0	-3827	0
10	0	0	0	0	0	0	0	0	0	9307	0	-9307	0	0
11	0	0	0	0	-2651	884	-1985	-662	0	0	6621	440	-1985	0
12	0	0	0	0	884	-295	-662	-221	0	-9307	440	10044	-662	0
13	0	0	0	0	0	0	0	0	-3827	0	-1985	-662	5812	0
14	0	0	0	0	0	0	0	0	0	0	0	0	0	1

Wektor

przemieszczeń

Wektor

obciążeń

węzłowych

Wektor

przemieszczeń

Wektor

obciążeń

węzłowych

u₁

d₁

Px₁

P₁

d₁

P₁

v₁

d₂

Py₁

P₂

d₂

P₂

u₂

d₃

Px₂

P₃

d₃

P₃

v₂

d₄

Py₂

P₄

d₄

P₄

u₃

d₅

Px₃

P₅

d₅

P₅

v₃

d₆

Py₃

P₆

d₆

P₆

u₄

= d =

d₇

Px₄

= P =

P₇

K^.

d₇

P₇

v₄

d₈

Py₄

P₈

d₈

P₈

u₅

d₉

Px₅

P₉

d₉

P₉

v₅

d₁₀

Py₅

P₁₀

d₁₀

P₁₀

u₆

d₁₁

Px₆

P₁₁

d₁₁

P₁₁

v₆

d₁₂

Py₆

P₁₂

d₁₂

P₁₂

u₇

d₁₃

Px₇

P₁₃

d₁₃

P₁₃

v₇

d₁₄

Py₇

P₁₄

d₁₄

P₁₄

Odwrócona macierz sztywności: K^-1

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1	0	0	0	0	0	0	0	0	0	0	0	0	0
2	0	1	0	0	0	0	0	0	0	0	0	0	0	0
3	0	0	0,0023	0	0,002	-0,002	0,0012	-0,002	0,0018	-0,0026	0,0019	-0,0026	0,0015	0
4	0	0	0	0,0003	0	0	0	0	0	0	0	0	0	0
5	0	0	0,002	0	0,002	-0,002	0,0012	-0,002	0,0018	-0,0026	0,0019	-0,0026	0,0015	0
6	0	0	-0,002	0	-0,002	0,0029	-0,0015	0,0029	-0,0018	0,003	-0,002	0,003	-0,0015	0
7	0	0	0,0012	0	0,0012	-0,0015	0,0012	-0,0016	0,0011	-0,0013	0,0013	-0,0013	0,0010	0
8	0	0	-0,002	0	-0,002	0,0029	-0,0016	0,0032	-0,0018	0,003	-0,002	0,003	-0,0015	0
9	0	0	0,0018	0	0,0018	-0,0018	0,0011	-0,0018	0,0018	-0,002	0,0017	-0,002	0,0015	0
10	0	0	-0,0026	0	-0,0026	0,003	-0,0013	0,003	-0,002	0,0055	-0,0023	0,0054	-0,0015	0
11	0	0	0,0019	0	0,0019	-0,002	0,0013	-0,002	0,0017	-0,0023	0,0019	-0,0023	0,0015	0
12	0	0	-0,0026	0	-0,0026	0,003	-0,0013	0,003	-0,002	0,0054	-0,0023	0,0054	-0,0015	0
13	0	0	0,0015	0	0,0015	-0,0015	0,0010	-0,0015	0,0015	-0,0015	0,0015	-0,0015	0,0015	0
14	0	0	0	0	0	0	0	0	0	0	0	0	0	1

	Wektor obciążeń węzłowych			Wynikowy wektor przemieszczeń
		0			0	u₁
K^.d = P		0			0	v₁
		0			0,890342281	u₂
czyli		0			0	v₂
		0			0,890342281	u₃
K^-1.P = d		-250			-1,186009	v₃
K^-1^.		0	=		0,559070278	u₄
		0			-1,18597045	v₄
		0			0,746947988	u₅
		-150			-1,58034355	v₅
		0			0,848766836	u₆
		0			-1,56422665	v₆
		0			0,603553696	u₇
		0			0	v₇

Wyznaczenie sił węzłowych K ^. d = P

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	d		Wynikowy wektor sił węzłowych
1	3083	1760	0	0	-1098	-1098	-1985	-662	0	0	0	0	0	0	0			0
2	1760	4421	0	-3102	-1098	-1098	-662	-221	0	0	0	0	0	0	0			216,64
3	0	0	3827	0	-3827	0	0	0	0	0	0	0	0	0	0,890342281			0
4	0	-3102	0	3102	0	0	0	0	0	0	0	0	0	0	0			0
5	-1098	-1098	-3827	0	11403	214	0	0	-3827	0	-2651	884	0	0	0,890342281			0
6	-1098	-1098	0	0	214	6047	0	-4654	0	0	884	-295	0	0	-1,186009			-250
7	-1985	-662	0	0	0	0	3970	1324	0	0	-1985	-662	0	0	0,559070278	=		0
8	-662	-221	0	0	0	-4654	1324	5096	0	0	-662	-221	0	0	-1,18597045			0
9	0	0	0	0	-3827	0	0	0	7654	0	0	0	-3827	0	0,746947988			0
10	0	0	0	0	0	0	0	0	0	9307	0	-9307	0	0	-1,58034355			-150
11	0	0	0	0	-2651	884	-1985	-662	0	0	6621	440	-1985	-662	0,848766836			0
12	0	0	0	0	884	-295	-662	-221	0	-9307	440	10044	-662	-221	-1,56422665			0
13	0	0	0	0	0	0	0	0	-3827	0	-1985	-662	5812	662	0,603553696			0
14	0	0	0	0	0	0	0	0	0	0	-662	-221	662	221	0			183,36

Wyznaczenie sił podłużnych w prętach kratownicy:

5. PORÓWNANIE OTRZYMANYCH WYNIKÓW

		z pkt 1 i 2	z pkt 4
[kN]	R_A	216,67	216,64
		N1	342,58	342,64
		N2	342,58	342,36
		N3	579,75	577,94
		N4	0,00	0,00
		N5	-550,00	-548,72
		N6	-550,00	-548,72
		N7	0,00	0,00
		N8	-459,62	-458,91
		N9	0,00	0,00
		N10	237,17	- 236,09
		N11	-150,00	-150,00
		R_B	183,33	183,36
cm	V₆	1,57	1,564

WM2 - Praca Projektowa nr 2 - Kratownica płaska- sem.IV, gr.3, st. zaoczne

0x01 graphic

Wyszukiwarka

Podobne podstrony:
Macierz sztywności
Macierz sztywności elementu prostokątnego oraz izoparametrycznego - referat
Macierz sztywności
macierz sztywnosci
Macierz sztywności
transformacja macierzy sztywności
macierz sztywności
MNzadania pp2 07, Znajdź metodą Kryłowa współczynniki wielomianu charakterystycznego macierzy
Schemat Ideowy Układu sterowania Agregatu Chłodniczego
Wybrane zagadnienia z zakresu przeszczepiania komórek macierzystych układu krwiotwórczego
Rozwoj serca i ukladu krazenie
Choroby układu nerwowego ppt
T7 Transformacja układu odniesienia
1 Bryła Sztywna Quizid 8461 ppt
Krew i choroby układu krwionośnego
Budowa Układu Okresowego Pierwiastków
fizjologia układu krążenia

więcej podobnych podstron