Laboratorium Fizyki I			Ćwiczenie nr: 37
						Data: 19.10.2005
Wydział: MCHTR	Grupa: 23	Zespół: 8	Punktacja	Przygotowanie: 4
Nazwisko i imię: Fiodorow Michał
Temat ćwiczenia: Falowe własności mikrocząsteczek					Sprawozdanie:
Prowadzący: M. Ćwil					Suma punktów:

1. Wiadomości wstępne:

Wykonane przez nas ćwiczenie dotyczyło falowych własności mikrocząsteczek.

Otóż począwszy od Einsteina pogląd na naturę fal elektromagnetycznych się zmienił. Okazało się że oprócz własności falowych, mają one także właściwości zbliżone do strumienia cząstek których pęd wyraża się wzorem:

p= h*v/c, bądź p= h/λ

gdzie h*v - energia fotonów; v, λ - częstotliwość i długość fali.

Taka własność nazywa się dualizmem falowo - korpuskularnym.

Należy wprowadzić także pojęcie fali de Broglie'a, reprezentujące poruszającą się cząstkę, którą w pewnych okolicznościach można traktować jako falę, o długości równej

λ= h/p

W ćwiczeniu wykorzystaliśmy także zjawisko dyfrakcji na sieci krystalicznej. Polega ono na tym iż każdy atom z płaszczyzny atomowej kryształu staje się źródłem nowej fali, które interferując ze sobą tworzą falę odbitą. Kryształ posiada oczywiście wiele płaszczyzn stąd zjawisko to może zachodzić w różny sposób. Jeśli kryształ zaczniemy obracać to zaobserwujemy na ekranie ustawionym za nim okręgi. Aby uniknąć obracania stasujemy polikryształy złożone z wielu krystalitów w których zawsze znajdzie się płaszczyzna atomowa spełniająca warunek Bragga:

2d sinΘ=n λ

Gdzie d - odległość między pł. at. ;

Θ - kąt pomiędzy prom. padającym a pł. at.

2. Przebieg ćwiczenia i jego cel.

Do zaobserwowania okręgów wykorzystaliśmy doświadczenie Thomsona. Polega ono na umieszczeniu w oscyloskopie cienkiej folii, w naszym przypadku aluminiowej i grafitowej, które mają własności polikryształu. Wiązka elektronów trafiając na folię podlega zjawisku opisanemu we wstępie co ostatecznie obserwowaliśmy jako okręgi na ekranie. Gdybyśmy mieli możliwość zmniejszenia natężenia wiązki elektronów do takiej wartości, że w przybliżeniu emitowane byłyby pojedyncze elektrony obserwowalibyśmy jedynie pojedyncze błyski. Jednak w naszym przypadku było to niemożliwe do uzyskania i mogliśmy jedynie uwierzyć w teorię.

W oscyloskopie mogliśmy regulować napięcie U, które przekładało się na zwiększenie energii przyspieszanych elektronów zgodnie z zależnością: E_k= e/U.

Biorąc pod uwagę fakt, że r>>D wzór Bragga w naszym przypadku wygląda trochę prościej:

dD/2r= nλ

gdzie D- śr okręgów; r- odl. folii od ekranu.

λ można obliczyć ze wzoru λ=h/p . Brakuje jeszcze pędu elektronu, który otrzymamy z zależności: eU= p²/2m skąd:

po przekształceniu wzoru Braga dochodzimy do zależności z której możemy wyznaczyć odległość międzyatomową d:

Doświadczenie przeprowadziliśmy dla sześciu różnych napięć i dla dwu różnych folii.

Dla folii aluminiowej (r=300±1mm) mierzyliśmy średnice czterech okręgów interferencyjnych. Oto wyniki pomiarów:

Lp.	U [kV]	D1	D2	D3	D4
1	14,59	24,5	28,5	40	47
2	14,12	25	29	40,5	48,5
3	13,59	25,5	29,5	42	49
4	12,24	28	31,5	44	51,5
5	11,54	28,5	32,5	46,5	54
6	10,54	29,5	34	48	56

Dane przerobiliśmy w ten sposób że zamias U wpisaliśmy

A średnice okręgów w cm zamieniliśmy na metry otrzymując:

Lp.	U [kV]	D1	D2	D3	D4
1	0,2618	0,245	0,285	0,4	0,47
2	0,26612	0,25	0,29	0,405	0,485
3	0,27126	0,255	0,295	0,42	0,49
4	0,28583	0,28	0,315	0,44	0,515
5	0,29437	0,285	0,325	0,465	0,54
6	0,30802	0,295	0,34	0,48	0,56

Wyniki po wstawieniu danych do programu Origin i wykonaniu wykresów dla poszczególnych wartości:

Program rozwiązał następujące równanie liniowe: Y = A + B * X,

gdzie Y to D, B to
, a X to
.

Dla D1:

Parameter Value Error

A -0,05354 0,02837

B 1,1445 0,10069

Dla D2:

A -0,03284 0,007

B 1,21312 0,02484

Dla D3:

A -0,07043 0,03093

B 1,7972 0,10979

Dla D4:

A -0,03116 0,02793

B 1,92425 0,09914

Więc np. opracowanie wyników i rachunek błędu dla D1 wygląda następująco:

B=1,1445, czyli

1,1445=
skąd d=

Wstawiając dane:

m= 9.1093897e-31 ± 5.4e-37 [kg];

e= 1.60217733e-19 ± 4.9e-26 [C];

h= 6.6260755e-34 ± 4.0e-40 [J s];

r= 300 [mm];

otrzymamy ostatecznie odległości międzypłaszczyznowe d w polikrysztale.

d=

natomiast błąd przypadkowy z programu Origin obliczony za pomocą średniej sumy kwadratów jest równy:

Δ(
)= {error}=0,10069

stąd można z kolei wyznaczyć błąd przypadkowy Δd_przyp obliczony przez program za pomocą średniej sumy kwadratów

natomiast błąd systematyczny należy obliczyć z różniczki zupełnej biorąc pod uwagę fakt, że d zależy od r, D i U.

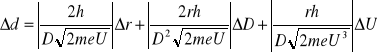
A oto wykresy dla D1, D2, D3 i D4(licząc od dołu do góry):

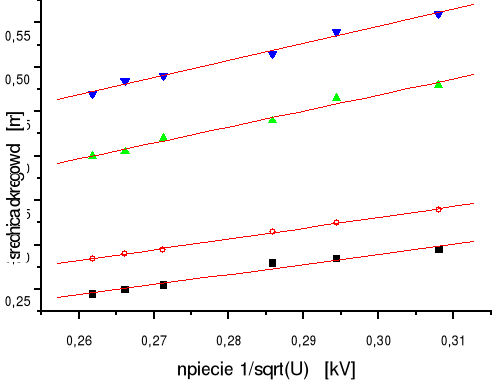
Dla folii grafitowej (r=127±1mm) wykonywaliśmy pomiary dwóch okręgów interferencyjnych. Oto wyniki pomiarów:

Lp.	U [kV]	D1	D2
1	9,12	16	26,5
2	7,96	17	28,5
3	7,14	18	30
4	6,36	18,5	31,5
5	5,59	20	33,5
6	5,25	20,5	35

Ponownie dane przerobiliśmy w ten sposób że zamiast U wpisaliśmy

A średnice okręgów w cm zamieniliśmy na metry otrzymując:

Lp.	U [kV]	D1	D2
1	0,33113	0,16	0,265
2	0,35444	0,17	0,285
3	0,37424	0,18	0,3
4	0,39653	0,185	0,315
5	0,42295	0,2	0,335
6	0,43644	0,205	0,35

Wyniki po wstawieniu danych do programu Origin i wykonaniu wykresów dla poszczególnych wartości:

Dla D1

Parameter Value Error

A 0,01947 0,00732

B 0,42456 0,01887

Dla D2

A 0,00727 0,00833

B 0,78006 0,02149

Rachunek błędów i opracowanie wyników wygląda podobnie jak w przypadku folii aluminiowej.

A oto wykresy dla D1 i D2

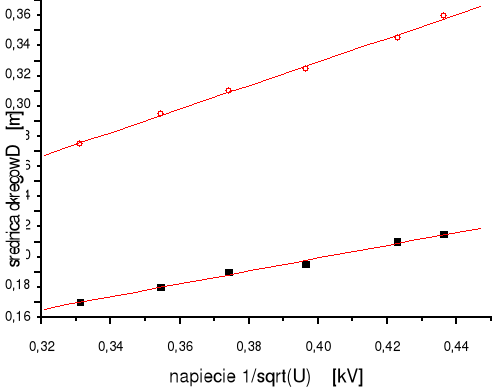
3. Wnioski:

Obserwacja okręgów dyfrakcyjnych pomogła nam uświadomić, że na cząstkę trzeba patrzeć w dwóch „płaszczyznach': cząsteczkowej i falowej, dlatego iż wykazuje właściwość zwaną dualizmem falowo- korpuskularnym. W takim razie ostatecznie można stwierdzić że hipoteza de Brogile'a jest prawidłowa, gdyż wiązka elektronów interferowała na folii aluminiowej jak i na grafitowej w sposób charakterystyczny dla fali fotonów. Wyniki odległości międzypłaszczyznowych w polikrysztale, które nam powychodziły są rzędu 10^-10 czyli mieszczą się w teoretycznych liczbach. Niestety odległości te nie są dokładnie wyliczone co jest wynikiem warunków laboratoryjnych, jak również (a w zasadzie przede wszystkim) niedokładności obserwatorów czyli studentów, którzy dopiero się uczą tego typu pomiarów.

---