Równanie ruchu płynu w formie różniczkowej
Rozpatrzymy postać całkową równania ruchu obszaru płynnego V ograniczonego zamkniętą powierzchnią płynną A, która wynika z zasady zmiany pędu:
![]()
.
Rozwiniemy wyrażenie opisujące jednostkową siłę powierzchniową, uwzględniając postać tensora naprężeń S:
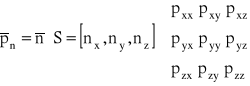
,
skąd mamy
![]()
.
Sumę (wypadkową) sił powierzchniowych działających na zamkniętą powierzchnię płynną A, która występuje w równaniu ruchu, można zatem przedstawić w postaci:
![]()
Każdą ze składowych powyższej sumy (przy wersorach ![]()
) można przedstawić w postaci sumy trzech całek i przekształcić na podstawie twierdzenia Greena-Gaussa-Ostrogradzkiego. Przykładowo:
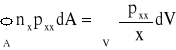
, 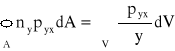
, 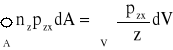
,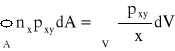
, itd.
Zapisując następnie przekształcone składowe sumy pod jednym znakiem całki, otrzymamy:
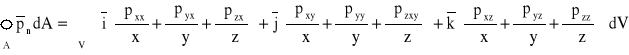
.
Funkcja, która występuje pod znakiem całki potrójnej po prawej stronie tego wyrażenia, może być przedstawiona jako iloczyn operatora Hamiltona (nabla) i tensora naprężeń. Zatem
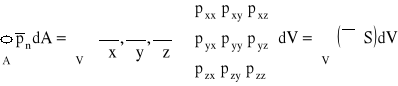
.
Wyrażenie ![]()
jest nazywane dywergencją tensora naprężeń.
Przekształconą postać wyrażenia opisującego sumę sił powierzchniowych uwzględnimy w równaniu ruchu obszaru płynnego V. Otrzymamy:
![]()
.
Zapisując pod jednym znakiem całki, mamy
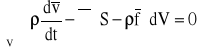
.
Powyższa całka musi być równa zeru dla dowolnych warunków brzegowych - ze względu
na dowolność przyjęcia obszaru płynnego V. Jest to możliwe tylko wtedy, gdy funkcja podcałkowa jest równa zeru, zatem:
![]()
.
skąd: ![]()
.
Jest to ogólne równanie różniczkowe ruchu płynu w postaci wektorowej. Jest ono równoważne trzem równaniom skalarnym, które są nazywane równaniami ruchu w naprężeniach:
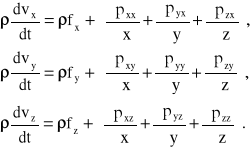
Równanie ruchu płynu nielepkiego (równanie Eulera)
Ogólne równanie ruchu płynu ma postać:
![]()
.
Jego szczególnym przypadkiem jest równanie Eulera, które dotyczy modelu płynu nielepkiego (μ:=0) i nieprzewodzącego ciepła (λ:=0). W płynie nielepkim nie mogą występować naprężenia styczne, a naprężenia normalne są równe (-p). Tensor naprężeń przyjmuje wówczas postać analogiczną jak dla płynu w spoczynku:
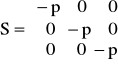
.
Dywergencja tensora naprężeń jest natomiast równa:
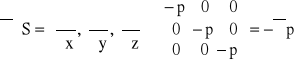
.
Równanie ruchu płynu przyjmuje wtedy postać:
![]()
.
Dzieląc obustronnie przez ρ otrzymamy równanie Eulera w postaci:
![]()
.
(Warto zauważyć, że dla ![]()
, otrzymamy z tego równania znane ze statyki równanie równowagi płynu w spoczynku: ![]()
- jako szczególny przypadek równania ruchu).
Dr inż. Janusz Bidziński Mechanika płynów - materiały pomocnicze dla studiów niestacjonarnych
1
Wyszukiwarka
Podobne podstrony:
Równanie Bernoulliego, simr, mechanika płynów, mechanika płynów
Całka i równane Eulera dla cieczy, mechanika plynów
17 równanie Eulera dla płynu nieściśliwego, mechanika plynów
Rownanie Eulera dla plynu doskonałego, mechanika plynów
Równanie Eulera dla płynu ściśliwego, mechanika plynów
Równanie równowagi płyny, mechanika plynów
równania różniczkowe, Akademia Morska -materiały mechaniczne, szkoła, Mega Szkoła, SEMESTR II, Matma
tchoń,mechanika analityczna,RÓWNANIA EULERA
Równanie równowagi płyny, mechanika plynów
17 równanie Eulera dla plynu niescisliwegoid 17345
Calka i równane Eulera dla cieczy
Równanie Eulera dla plynu scisliwego
Tematyka kolokwium z MP - materiał wykładów, simr, mechanika płynów, mechanika płynów
06 Calki rownania Euleraid 6268 Nieznany (2)
ćw.5 Kawitacja PRO, SiMR, mechanika płynów, Mechanika Płynów Sprawozdania
Zastosowanie dynamicznych równań Eulera i równania Bernouliego w zadaniach
Mechanika płynów - podstawowe pojęcia 2, simr, mechanika płynów, mechanika płynów
mechanika płynów ściąga, SiMR, Mechanika płynów
więcej podobnych podstron