Politechnika Śląska Wydział Elektryczny Laboratorium Automatyki i Sterowania	Rodzaj studiów: EL Rok akademicki 2006/07 Semestr VI
Temat: Modelowanie obiektów ciągłych w dziedzinie czasu
Studenci: Danuta Szpetman Grzegorz Pudło Robert Ligocki Przemysław Kasprzyk	Data wykonania: 28.02.07 Grupa: EE1 Sekcja 1

I) PROGRAM ĆWICZENIA

Naszym zadaniem było zapoznanie się z układami ciągłymi pierwszego i drugiego stopnia oraz parametrami jakie wpływały na ów układy. Ćwiczenie wykonywaliśmy przy użyciu programu MATLAB z bibliotekami SIMULINK.

II) WYLICZENIA ORAZ KONSTRUKCJA UKŁADU POMIAROWEGO

A) Dla układu pierwszego rzędu:

(*)

Z powyższego równania otrzymujemy schemat układu pomiarowego dla układu ciągłego pierwszego rzędu:

Wyliczenie transmitancji K(s):

Dzielimy równanie (*) prze A₀ otrzymując:

stąd:

T - stała czasowa

k - wzmocnienie

ostatecznie:

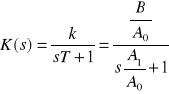
B) Dla układu drugiego rzędu:

(**)

Z powyższego równania otrzymujemy schemat układu pomiarowego dla układu ciągłego drugiego rzędu:

Wyliczenie transmitancji K(s):

Dzielimy równanie (**) prze A₂ otrzymując:

stąd:

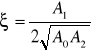
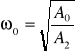
k - wzmocnienie

ξ - stopień tłumienia

ω₀ - pulsacja drgań własnych nietłumionych

ostatecznie:

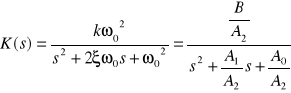
III) POMIARY I WYKRESY

Dla układu pierwszego rzędu w odpowiedzi na skok jednostkowy:

A₀ = 1 1/A₁ = 1 B = 1

t (s)

A₀ = 6 1/A₁ = 0,5 B = 15

t (s)

A₀ = 0,85 1/A₁ = 0,76 B = 10

t (s)

A₀ = 0,01 1/A₁ = 0,76 B = 10

t (s)

A₀ = 2 1/A₁ = 0,9 B = 0,5

Dla układu pierwszego rzędu w odpowiedzi na przebieg sinusoidalny

(A₀ = 2 1/A₁ = 0,9 B = 1)

f (rad/s) = 50

t (s)

f (rad/s) = 1

t (s)

f (rad/s) = 2

t (s)

Dla układu drugiego rzędu w odpowiedzi na skok jednostkowy:

A₀ = 1 A₁ = 1 1/A₂ = 1 B = 1

t (s)

A₀ = 1 A₁ = 1 1/A₂ = 0,2 B = 1

t (s)

A₀ = 5 A₁ = 1 1/A₂ = 0,5 B = 10

t (s)

A₀ = 5 A₁ = 0,7 1/A₂ = 5 B = 10

t (s)

IV) WNIOSKI

Z powyższych wykresów możemy wywnioskować, iż:

W przypadku układu pierwszego rzędu zmieniając parametry B i A₀, czyli wpływając na współczynnik wzmocnienia k, regulujemy wartość, do jakiej dąży przebieg odpowiedzi układu na skok jednostkowy. Natomiast zmieniając parametry A₁ i A₀ wpływaliśmy na stałą czasową T układu, przez co regulowaliśmy czas ustalenia się przebiegu odpowiedzi układu na skok jednostkowy (im T było większe tym dłużej ustalał się przebieg). Na przebiegach odpowiedzi na sygnał sinusoidalny zaobserwowaliśmy, iż wzrost częstotliwości sygnału wejściowego powodował na wyjściu wprowadzenie składowej zanurzeniowej, która zanikała po pewnym czasie. Dla niskich częstotliwości składowa ta jest praktycznie niezauważalna.

W przypadku układu drugiego rzędu zmieniając parametry B i A2 wpływaliśmy na wzmocnienie k układu, które jak w przypadku układu pierwszego rzędu odpowiada za wartość do jakiej darzy odpowiedz układu. Zmieniając pozostałe parametry, czyli A₀, A₁ oraz również A₂ wpływaliśmy na tłumienie układu ξ i pulsację drgań własnych nietłumionych ω₀ układu. Od tych dwóch parametrów zależy czy układ jest oscylacyjny czy inercyjny (czyli czy układ ma tendencję do oscylacji czy też stabilizacji sygnału wyjściowego).

4

y(t)

B

y`(t)

x(t)

B

A₀

A₁

1/A₂

+

-

1/A₁

1/s

x(t)

y``(t)

y`(t)

1/s

-

+

-

1/s

y(t)

A₁

---