Nr ćwicz.: 5	Politechnika Radomska im. Kazimierza Pułaskiego w Radomiu Laboratorium z Chemii Fizycznej		Wydział MiTO I sem._I Rok akademicki
Data ćwicz: .02.04.2001
Nazwisko Imię: Wachowicz Paweł	Temat ćwiczenia: Wyznaczanie współczynnika podziału Nernsta i przybliżonej stałej równowagi.		2000/2001
Zasada Sobiesław
Numer grupy ćwiczeniowej	Sprawozdanie oddano dnia	OCENA	Prowadzący
X

1. Cel ćwiczenia:

Celem ćwiczenia jest wyznaczenie współczynnika podziału Nernsta i przybliżonej stałej równowagi.

2. Część teoretyczna:

Ekstrakcja polega na przeprowadzeniu substancji z jednej fazy, w której jest ona zawieszona lub rozpuszczona do drugiej fazy ciekłej. Podczas kontaktu roztworu lub zawiesiny substancji w jakimś rozpuszczalniku z innym nie mieszającym się z nim rozpuszczalnikiem substancja ta dyfunduje przez granicę faz. Po ustaleniu się stanu równowagi stężenia substancji w obu fazach ( c_a i c_b ) są w przybliżeniu wprost proporcjonalne do stosunku rozpuszczalności substancji w tych rozpuszczalnikach ( odpowiednio r_a i r_b ). Współczynnikiem proporcjonalności jest tu współczynnik podziału k.

Aby ekstrakcja była jak najskuteczniejsza, korzystniej jest przeprowadzić ją wielokrotnie przy użyciu mniejszych porcji rozpuszczalnika niż jednorazowo większą jego porcją. Dobry rozpuszczalnik do ekstrakcji z roztworów wodnych powinien wykazywać duży współczynnik podziału w układzie z wodą, żle rozpuszczać się w wodzie oraz istotnie różnić się temperaturą wrzenia od substancji ekstrahowanej. Najkorzystniejsze są rozpuszczalniki o dość niskiej temperaturze wrzenia, można je wówczas bowiem łatwo oddzielić od substancji ekstrahowanej przez odparowanie lub destylację. Ponadto rozpuszczalnik taki powinien roztwory różniące się znacznie gęstością od roztworu ekstrahowanego i nie wykazywać tendencji do tworzenia emulsji, utrudniając rozdzielenie faz w rozdzielaczu. Ponieważ dyfuzja zachodzi na granicy faz, należy stosować energiczne wstrząsanie powodujące rozwinięcie powierzchni tej granicy.

Jeżeli w danym układzie temperatura jest stała (T=const.), a reakcja przebiega zgodnie z równaniem:

aA + bB
cC + dD

to po osiągnięciu stanu równowagi stężenia reagentów wyrażone w stężeniach molowych spełniają zależność:

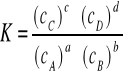
W równaniu tym stałą K nazywamy stałą równowagi reakcji. Stałej tej najczęściej używa się w przypadku rozpatrywania równowag w roztworach, a więc w układach, które najczęściej znajdują się pod stałym ciśnieniem atmosferycznym, a równocześnie zachowują stałą objętość. Zatem można stąd wysnuć wniosek, że im większa jest stała równowagi tym większe są stężenia produktów reakcji w stanie równowagi.

III. Wykonanie ćwiczenia:

Do pierwszego rozdzielacza wlewam 5 cm³ nasyconego roztworu jodu w czterochlorku węgla i 75 cm³ wody destylowanej, do drugiego 10 cm³ roztworu jodu i 50 cm³ 0,1 molowego roztworu jodku potasu (KJ). Przeprowadzam ekstrakcję wstrząsając rozdzielaczami przez kilka minut i odstawiam do rozdzielenia się faz.

Następnie po rozdzieleniu się warstw z pierwszego rozdzielacza przelewam do kolbki stożkowej warstwę czterochlorkową. Stąd pobieram 2 cm³ roztworu, przelewając do zlewki dodaję 10 cm³ 0,1 molowego roztworu KJ, całość wstrząsam i miareczkuję 0,1 molowym roztworem Na₂S₂O₃ aż obie warstwy staną się całkowicie bezbarwne.

Miareczkuję także warstwę wodną z pierwszego rozdzielacza, biorąc do tego celu 50 cm³ roztworu, a pod koniec miareczkowania dodaję 1 cm³ roztworu skrobi.

Z drugiego rozdzielacza również zlewam warstwę czterochlorkową do kolbki i miareczkuję ją oraz warstwę wodną biorąc do tego celu po 5 cm³ odpowiednich roztworów przy czym podczas tego miareczkowania postępuję tak, jak w przypadku pierwszego.

IV. Wyniki:

• Reakcja odbarwienia roztworu jodu przez roztwór tiosiarczanu (Na₂S₂O₃) przebiega następująco:

Rozdzielacz pierwszy:

- do zmiareczkowania warstwy czterochlorkowej zużyłem 2,2 cm³ 0,1 molowego roztworu Na₂S₂O₃

- do zmiareczkowania warstwy wodnej zużyłem 2 cm³ 0,1 molowego roztworu Na₂S₂O₃.

Z reakcji podanej powyżej wynika, że na zmiareczkowanie jednego mola jodu potrzeba dwa mole tiosiarczanu sodu. Stąd wynika zatem, że: skoro w 1000 cm³ roztworu Na₂S₂O₃ znajduje się 0,1 mola jonów S₂O₃^2-, to w 2,2 cm³ musi znajdować się 2,2·10^-4 mola tych jonów. Zatem stężenie jodu w warstwie czterochlorkowej po ekstrakcji wynosiło dwa razy mniej tj. 1,1·10^-4 mola.

Analogiczne rozumowanie przeprowadzam dla warstwy wodnej i otrzymuję, że stężenie jodu w warstwie wodnej po ekstrakcji wynosiło: 10^-4 mola.

Zatem współczynnik podziału jodu pomiędzy czterochlorek węgla i wodę wynosi:

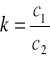
Rozdzielacz drugi:

- do zmiareczkowania warstwy czterochlorkowej zużyłem 3,8 cm³ 0,1 molowego roztworu Na₂S₂O₃

- do zmiareczkowania warstwy wodnej zużyłem 0,8 cm³ 0,1 molowego roztworu Na₂S₂O₃

W drugim rozdzielaczu będziemy mieć po ekstrakcji - 1,9·10^-4 moli jonów jodkowych w warstwie czterochlorkowej

- 4·10^-5 moli jonów jodkowych w warstwie wodnej.

A więc współczynnik podziału będzie wynosił:

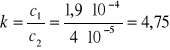
W roztworze wodnym zaszła reakcja zgodnie z równaniem:

KJ + J₂ = KJ₃

Reakcja ta ustaliła się na pewnym stałym poziomie i przebiegała w stałej temperaturze, a zatem możemy obliczyć dla niej stałą równowagi według wzoru podanego w części teoretycznej modyfikując go nieco. I tak oznaczając za:

- sumaryczne stężenie J₂+KJ₃ w warstwie wodnej

- stężenie J₂ w warstwie wodnej

- początkowe stężenie jodku potasu

- współczynnik podziału jodu między wodę i czterochlorek węgla.

Jeżeli teraz podstawimy te dane do wzoru głównego będziemy mieć:

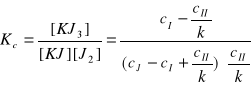
W naszym przypadku wartości te wynoszą odpowiednio:

c_I = 1,6ּ10^-4

c_II = 1,9ּ10^-4

c_J = 0,1 mol/l

k = 4,75

a więc:

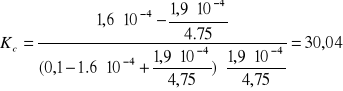
Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---