Cw.1. Przeprowadzić analizę wyników pomiarów geodezyjnych:

1. Wyznaczyć wartości czterech kątów wypełniających horyzont wokół dowolnego punktu,

• do obliczeń przyjąć dowolne wartości współrzędnych płaskich x, y;

• wartości współrzędnych wyrazić liczbami przynajmniej o 6 cyfrach znaczących;

• wartości kątów wyrazić w mierze stopniowej i gradowej;

• przeprowadzić obliczenia kontrolne.

• Wyznaczyć wartości trzech kątów w trójkącie mając dowolne długości trzech boków. Kąty wyrazić w mierze stopniowej i gradowej.

3. Wyznaczyć wartości trzech kątów w trójkącie. Przyjąć dowolne wartości współrzędnych punktów wierzchołkowych w układzie przestrzennym x, y, z.

Kąty wyrazić w mierze stopniowej i gradowej.

4. Wyznaczyć wartości trzech kątów w trójkącie. Przyjąć dowolne wartości współrzędnych punktów wierzchołkowych w układzie geograficznym
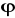
   i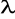
   . Kąty wyrazić w mierze stopniowej i gradowej z dokładnością 0,01” i 0,01^cc.

5. Wyznaczyć wartości współrzędnych punktów stosując wzory dla wcięcia:

• W przód

• Wstecz

• Liniowego

• Azymutalnego

Do obliczeń przyjąć dowolne wartości współrzędnych płaskich x, y i dowolne wartości kątów w mierze stopniowej lub gradowej. Wartości współrzędnych wyrazić liczbami o 6- cyfrach znaczących.

6. Zamiana współrzędnych lokalnych na terenowe. Wyznaczyć wartości współrzędnych 10 punktów w układzie wtórnym.

Do obliczeń przyjąć dowolne wartości współrzędnych płaskich x, y w układzie pierwotnym oraz, dowolne wartości dwóch punktów w układzie wtórnym. Wartości współrzędnych wyrazić liczbami o 6 cyfrach znaczących.

7. Sporządzić sprawozdanie.

8. Zaliczyć test sprawdzający.

Uwaga! W każdym analizowanym przypadku sporządzić szkic.

Sposób generacji współrzędnych punktów.

Rysujemy osie układu współrzędnych xy. Następnie wybieramy pięć punktów A, B, C, D, E. Rozkład punktów powinien odpowiadać mniej więcej temu na poniższym rysunku. Współrzędne punktów A, B, C, D, E można wyznaczyć mierząc ich odległości od początku układu przykładowo linijką.







Tabela 2. Współrzędne punktów pomnożone przez 100.
	x [m]	y [m]
A	410	420
B	1340	220
C	1570	1340
D	610	1520
E	850	1070

Tabela 1. Współrzędne punktów z rysunku.
	x [cm]	y [cm]
A	4,1	4,2
B	13,4	2,2
C	15,7	13,4
D	6,1	15,2
E	8,5	10,7

Tabela 3. Współrzędne punktów o zwiększonej dokładności (przynajmniej 6 cyfr znaczących)
	x [m]	y [m]
A	412,234	425,876
B	1347,534	228,654
C	1578,209	1340,432
D	614,023	1528,123
E	857,893	1073,601

Do współrzędnych tabeli 2 dodajemy wybrane losowo z przedziału 0- 9 liczby mające trzy cyfry po przecinku. Przykładowo do 410 dodajemy liczbę 2,234, a do 1340 liczbę 7,534.

1

0

2

4

6

8

10

12

14

16

0

2

4

6

8

10

12

14

16

y

x

B(13,4; 2,2))

D(6,1;15,2)

C(15,7;13,4)

A(4,1;4,2))

E(8,5; 10,7)

---