Metoda stabilizacyjna
Obliczenie linii kontrolnych:
Obliczam wartość średnią:
x = ![]()
xi Dla k = 34 (ilość próbek)
x =[(-16,82)+(-15,08)+(-12,44)+(-0,42)+ 7,32 +(-1,16)+(-7,16)] = = -1,3459
Otrzymana średnia jest jednocześnie linią centralną na karcie kontrolnej:
![]()
=![]()
= -1,3459
Linia centralna dla rozstępu:
![]()
= ![]()
Dla k = 34 (ilość próbek)
![]()
= (11,7+11,8+11,3+12,3+10,5+12,1+7) = = 2,2559
Do obliczenia linii kontrolnych górnych xg i dolnych xd przyjmuje współczynnik t = 3
Dla karty kontroli wartości średniej:
Zewnętrzna górna linia kontrolna:
Xg = ![]()
+ A2![]()
Współczynnik A2 = 0,577 (z tabel);
Stąd:
Xg = -1,3459 + 0,577 . 2,2559 = -0,0442
Zewnętrzna dolna linia kontrolna:
Xd = ![]()
- A2![]()
Wsp. A2 = 0,577
Stąd:
Xd = -1,3459 - 0,577 . 2,2559 = -2,6477
Wewnętrzna górna linia kontrolna:
Xg, = ![]()
+ A2, ![]()
Wsp. A2, = 0,377 (z tabel);
Stąd:
Xg, = -1,3459 + 0,377 . 2,2559 = -0,4954
Wewnętrzna dolna linia kontrolna:
Xd, = ![]()
- A2, ![]()
Wsp. A2, = 0,377 (z tab.);
Stąd: Xd, = -1,3459 - 0,377 . 2,2559 = -2,1964
Dla karty kontroli rozstępu:
Zewnętrzna górna linia kontroli:
Rg = D2 ![]()
Dla D2 = 2,11 (z tabel);
Stąd:
Rg = 2,11 .2,2559 = 4,7599
Wewnętrzna górna linia kontrolna:
Rg, = D2, ![]()
Dla D2, = 1,66 (z tab.):
Stąd:
Rg, = 1,66 . 2,2559 = 3,7448
Natomiast dolne linie kontrolne zewnętrzną i wewnętrzną ustala się jako 0.
Po obliczeniu wszystkich niezbędnych wartości można wykonać kartę kontroli x - R
Metoda projektowa:
Nie zostały nam narzucone wartości wymiarów granicznych potrzebnych np. do wyznaczenia linii centralnej. Dlatego wartości wymiarów granicznych przyjmuje w oparciu o wyniki uzyskane podczas ćwiczenia, stąd: A=-4; B=+4
Obliczam linię centralną:
Xc= = 4
Obliczam linie kontrolne (górną i dolną) ze wzorów:
Xg = B - e
gdzie: e = S (B-A)
Xd = A + e
Przyjmując stopień wadliwości w=0,5%, i współczynnik t=2,81 ⇒ wsp. S = 0,261 (dla próbki n=5)
Po podstawieniu otrzymujemy:
Xg= B - e = 1,912
Xd= A+ e = -1,912
Następnie należy sprawdzić czy można zaprojektować kartę kontrolną dla tej produkcji . Będzie to możliwe gdy odchylenie średnie spełni poniższą nierówność:
σ ≤ gdzie wsp. t![]()
= 2,81
Aby sprawdzić powyższy warunek należy obliczyć odchylenie standardowe, według wzoru:
σ =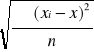
Po podstawieniu otrzymujemy:
σ = ![]()
= 2,218
![]()
= ![]()
= 1,423
Po wyznaczeniu powyższych danych można również obliczyć wskaźnik zdolności procesu - Cp, w celu przeprowadzenia badania zmienności procesu.
Cp = ![]()
=![]()
0,6
Analizując powyższe wyniki widać, że warunek σ ≤ nie został spełniony, a co za tym idzie nie można zaprojektować karty kontrolnej dla tej produkcji. Również wskaźnik zdolności procesu informuje nas o braku tej zdolności, gdyż minimalna wartość tego wskaźnika wynosi 1.
Wnioski:
Przeprowadzenie tego ćwiczenia pokazało, że statystyczna kontrola jakości i sporządzane w niej karty kontrolne są prostym sposobem czuwania nad jakością. Graficzne przedstawienie wyników umożliwia szybką ocenę jakości całej partii np. produkowanych przedmiotów. Analizując kartę kontroli można stwierdzić gdzie zostały przekroczone linie graniczne ostrzegające o możliwości wystąpienia sygnału o rozregulowaniu oraz moment kiedy trzeba zatrzymać proces i usunąć usterkę.
Analizując otrzymane wyniki w karcie kontroli rozstępu widać, że raz pojawił się sygnał uprzedzający, a 2-krotnie sygnał świadczący o rozregulowaniu. Pojawienie się sygnału o rozregulowaniu powinno spowodować przerwanie produkcji i usunięcie przyczyny jego wystąpienia.
Natomiast analizując kartę kontroli wartości średniej wg met. stabilizacyjnej widać całkowite rozregulowanie procesu. Wpływ na taki kształt karty miały na pewno próbki nr 4 i 19, w których uzyskano pomiary o dużych rozbieżnościach. Trudno wyjaśnić przyczyny tak dużych różnic między mierzonymi wałeczkami, możliwe że nastąpił błędny odczyt pomiarów lub niewłaściwe działanie czujnika.
Otrzymanie tak bardzo różniących się pomiarów sprawiło, że nie można zaprojektować karty kontroli wartości średniej wg met. projektowej. Świadczy o tym np. wskaźnik zdolności procesu, którego wartość wynikająca z obliczeń wyniosła 0,6 natomiast minimalna wartość tego współczynnika wynosi 1.
Laboratorium z metrologii
Data wykonania ćwiczenia:
8.X.2003
Skład grupy:
Akuszewski Grzegorz
Kaczmarek Krzysztof
Ocena:
Temat ćwiczenia:
Statystyczna kontrola jakości
Wyszukiwarka
Podobne podstrony:
SPRAWOZDANIE NR 1, ZiIP, II Rok ZIP, Metrologia, Sprawozdanie nr 1
sprawozdanie nr 5, ZiIP, II Rok ZIP, Metrologia, Sprawozdanie nr 5
SPRAWOZDANIE NR 1, ZiIP, II Rok ZIP, Metrologia, Sprawozdanie nr 1
metrologia - błędy kształtu, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
str tytuł-SKJ, ZiIP, II Rok ZIP, Metrologia, SKJ-Statystyczna Kontrola Jakości, Sprawozdanie
Stożki, ZiIP, II Rok ZIP, Metrologia
częstotliwość, ZiIP, II Rok ZIP, Metrologia
SKJ wnioski, ZiIP, II Rok ZIP, Metrologia, SKJ-Statystyczna Kontrola Jakości, Sprawozdanie
sprawozdanie nr 3, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdanie nr 3
Kopia LABORATORIUM-nasze, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1
LABORATORIUM, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1), Sprawozda
Pomiary błędów kształtu, ZiIP, II Rok ZIP, Metrologia
LABORATORIUM-nasze v2, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1),
Politechnika Poznańska, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania, Statystyczna kontrol
POPRAWIONE 01 - Pomiary współrzędnościowe, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
Pomiary stożków, ZiIP, II Rok ZIP, Metrologia
SKJ, ZiIP, II Rok ZIP, Metrologia, SKJ-Statystyczna Kontrola Jakości, Sprawozdanie
Błędy pomiarów pośrednich, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
metrologia -r-a, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
więcej podobnych podstron