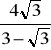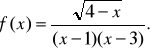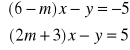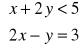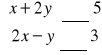MATEMATYKA część 1 |
19
|
99 |
|
A GDYBY MATURA BYŁA W PIERWSZEJ KLASIE SZKOŁY ŚREDNIEJ ... |
|
|
|
Twój nauczyciel określi, które zadania należy rozwiązać i w jakim czasie. Za poprawne rozwiązanie każdego pojedynczego zadania otrzymasz 3 punkty. Przed oddaniem nauczycielowi rozwiązań zadań, wpisz obok tematu każdego z zadań liczbę punktów, którą spodziewasz się uzyskać. Zsumuj wszystkie te punkty. Ciekawe, czy ocena dokonana przez nauczyciela potwierdzi Twoją prognozę. |
|
||
Życzymy Ci powodzenia!!!
|
|
Twoje punkty |
|
Wyznacz zbiory |
|
||
Oblicz x ze wzoru |
|
||
Przekształć wyrażenie |
|
||
Zapisz za pomocą nierówności z wartością bezwzględną warunek: |
|
||
Rozwiąż nierówność |
|
||
Dane są wektory |
|
||
Cenę dywanu kosztującego pierwotnie 500 zł obniżono o 20%. W miesiąc później obniżono jeszcze o 15%. O ile procent łącznie obniżono pierwotną cenę tego dywanu? |
|
||
Agnieszka jest o cztery lata młodsza od Kasi. Za sześć lat będą miały razem 34 lata. Ile lat ma obecnie każda z dziewcząt? |
|
||
Określ dziedzinę funkcji |
|
||
Obok dany jest wykres funkcji Odczytaj z wykresu
|
|
|
|
Napisz równanie prostej, do której należą punkty |
|
||
Dana jest funkcja |
|
||
Dla jakiej wartości parametru m układ równań |
|
||
Oblicz wartość wyrażenia |
|
||
Dane są punkty:
|
|
||
W trójkącie równoramiennym miara |
|
||
W równoległoboku ABCD dane są współrzędne punktów |
|
||
Z trzech okręgów o środkach A, B, C każdy jest styczny zewnętrznie do dwóch pozostałych. Znając odległości środków |
|
||
W przekształceniu P płaszczyzny obrazem odcinka |
|
||
Czworokąt ABCD jest wpisany w okrąg o środku O tak jak na rysunku obok. Oblicz miary trzech kątów:
|
|
|
|
|
Imię i nazwisko: |
Twoja suma punktów: |
|
MATEMATYKA część 2 |
19
|
99 |
|
A GDYBY MATURA BYŁA W PIERWSZEJ KLASIE SZKOŁY ŚREDNIEJ ... |
|
|
|
Twój nauczyciel określi, które zadania należy rozwiązać i w jakim czasie. Za poprawne rozwiązanie każdego pojedynczego zadania otrzymasz 10 punktów. Przed oddaniem nauczycielowi rozwiązań zadań, wpisz obok tematu każdego z zadań liczbę punktów, którą spodziewasz się uzyskać. Zsumuj wszystkie te punkty. Ciekawe, czy ocena dokonana przez nauczyciela potwierdzi Twoją prognozę. |
|
||
Życzymy Ci powodzenia!!!
|
|
Twoje punkty |
|||
Dana jest funkcja
|
|
||||
Dane są trzy niewspółliniowe punkty O, A i B.
Wyznacz zbiór wszystkich punktów odległych o długość
|
|
||||
Rozwiąż zadanie z konkursu dla uczniów zorganizowanego przez pewien Bank. "Dysponując podaną niżej ofertą naszego Banku podejmij decyzję jaki typ lokaty wybrać i na jaki okres ulokować kapitał 2000 zł, by najszybciej i najkorzystniej uzyskać z odsetek kwotę 500 zł." |
|
||||
Typ lokaty |
Uwagi |
Oprocentowanie w stosunku rocznym |
|
||
A |
Kapitalizacja odsetek co 1 miesiąc |
18% |
|
||
B |
Kapitalizacja odsetek co 3 miesiące |
19% |
|
||
C |
Kapitalizacja odsetek co 6 miesięcy |
20% |
|
||
D |
Kapitalizacja odsetek co 1 rok |
21% |
|
||
Dany jest układ nierówności i równania liniowego z dwiema niewiadomymi
|
|
||||
|
Imię i nazwisko: |
Twoja suma punktów: |
|
||
Wyszukiwarka
Podobne podstrony:
Zadania z treścia
Prezentacja 2 analiza akcji zadania dla studentow
Przedmiot i zadania dydaktyki 4
zadanie 1 v 002
Przedmiot dzialy i zadania kryminologii oraz metody badan kr
KOLOKWIUM 2 zadanie wg Adamczewskiego na porownawczą 97
CELE I ZADANIA EDUKACJI MEDIALNEJ(1)
ochrona atmosfery zadania
zadania
Przedmiot i zadania dydaktyki 2
Wymogi, cechy i zadania sprawozdawczośći finansowej
ZADANIA PiP Prezentacja Microsoft PowerPoint
1F CWICZENIE zadanie wg Adamczewskiego na porownawczą 97id 18959 ppt
zadania i rozwiazania z przekrojów 2
zadania egzaminacyjne
ZADANIA WÓJTA I STAROSTY W ZARZĄDZANIU KRYZYSOWYM
Motywacja zadaniowa[1]
więcej podobnych podstron