1.Część teoretyczna

1.1.Lepkość cieczy.

Każde ciało poruszające się w cieczy czy gazie doznaje pewnej hamującej siły wskutek tego, że warstewki cieczy przylegające do ciała będącego w ruchu pociągają za sobą coraz dalsze warstewki sąsiednie. Podobnie jak w przypadku przepływu cieczy przez rurki kapilarne mamy tu do czynienia z przesuwaniem się jednych warstewek cieczy względem drugich. Istnieje spad prędkości cząsteczek cieczy w kierunku prostopadłym do kierunku ruchu.

Siła która wywołuje ten spad prędkości, ma swe źródło w przyciąganiu międzycząsteczkowym. Jest ona czynnikiem hamującym ruch, przypisujemy jej zatem zwrot przeciwny kierunkowi ruchu i nazywamy ją tarciem wewnętrznym cieczy albo lepkością - w odróżnieniu od tarcia zewnętrznego, z którym mamy do czynienia wówczas, gdy dwie powierzchnie różnych ciał poruszają się względem siebie.

Prawo Stokesa, według którego gładka kulka o promieniu r, poruszająca się w cieczy ze stałą prędkością v doznaje oporu tarcia T skierowanego przeciwnie względem v, wyraża się wzorem:

Ft=-6phrv. Wielkość h jest niezależna od materiału, zktórego wykonano kulke, zależy natomiast od rodzaju cieczy i bardzo silnie od jej temperatury. Ruchy termiczne cząstek mają wpływ na siły oddziaływania międzycząsteczkowego. W cieczach wzrost prędkości ruchów termicznych siły te osłabia (h maleje), w gazach sytuacja jest odwrotna, ze wzrostem temperatury współczynnik lepkości wzrasta, gdyż przy wzroście temperatury rosną prędkości cząsteczek.

Wielkość h, stała dla danej cieczy i temperatury, nosi nazwę współczynnika lepkości lub tarcia wewnętrznego cieczy. Jeżeli kulka wykonana jest z materiału o gęstości r większej od gęstości rp płynu, to ruch może następować na skutek działania siły ciężkości:

Ponieważ jednak kulka spada, w ośrodku płynnym działa na nią dodatkowo siła wyporu Fw, która zgodnie z prawem Archimedesa wyraża się wzorem:
. Sumując wszystkie siły działające na kulkę otrzymamy: F=Fg+Fw+Ft, czyli
.

Siła Stokesa zależy od prędkości i istnieje taka prędkość vo, przy której siła F jest równa zeru, co oznacza, że kulka porusz się ruchem jednostajnym (I-sza zasada dynamiki). Jeżeli prędkość jest różna od vo, to kulka porusza się ruchem przyspieszonym i jej prędkość wzrasta lub maleje do chwili osiągnięcia wartości vo. Równanie: Ft=-6phrv, stosuje się ściśle tylko w przypadku, gdy kulka porusz się w ośrodku o nieograniczonej szerokości i gdy mamy do czynienia z ruchem laminarnym. W przypadku, gdy kulka porusza się w rurze o promieniu rk, wypełnionej cieczą, wtedy równanie Stokesa przyjmuje postać: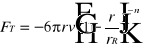
. Uwzględniając tę poprawkę w równaniu na sumę sił działających na kulkę i zakładając F=0 oraz v=l/t, gdzie t jset czasem spadania kulki, otrzymujemy: .

Spadek kulki w płynie ulega znacznemu zwolnieniu w rurce ośrednicy nieznacznie przekraczającej średnicę kulki. Wtedy rurkę musimy ustawić nieco ukośnie, gdyż przy ustawieniu pionowym ruch kulki nie jest jednostajny. Przy ustawieniu skośnym kulka toczy się po ściance rurki. Do omawianego przypadku stosuje się wzór zapisany w postaci: h=K(rk-ro)t, gdzie K jest stałą przyrządu, którą wyznaczamy z pomiaru wykonanego dla płynu o znanym współczynniku lepkości. Współczynnik lepkości zależy w dużym stopniu od temperatury. Dla cieczy zależnością tą rządzi prawo: , gdzie T jset temperaturą w skali Kelvina, A i B - stałe charakteryzujące ciecz.

Wizkozymetr Höplera składa się z rurki, w której mierzymy czas spadku kulki, otoczonej płaszczem wodnym. Temperaturę wody regulujemy ultratermostatem. Jeden z korków zamykających rurkę jest wydrążony i zaopatrzony w wentyl. W temperaturze pokojowej wydrążenie to pozostaje puste. W miarę podgrzewania objętość cieczy wzrośnie i wydrążenie wypełnia sie, a ciśnienie wzrasta tylko nieznacznie. Pomiar czasu opadania kulki można powtarzać wielokrotnie. Wystarczy każdorazowo obrócić przyrząd o kąt p wokół osi. Śruba znajdująca się z tyłu przyrządu służy do unieruchomienia rurki. Poziomica służy do kontroli ustawienia przyrządu.

Poprawne wyniki uzyskuje się tylko wtedy, gdy przyrząd jest bardzo czysty. Stąd przed pomiarem należy wnętrze rurki oraz kulkę dokładnie oczyścić i przemyć alkoholem lub eterem. Ciecz przeznaczoną do pomiaru należy wygotować, by w ten sposób pozbawić ją resztek gazów, zakłócających pomiar. Przed rozpoczęciem pomiarów ciecz badaną wygotowujemy, ochładzamy do temperatury pokojowej, po czym wypełniamy rurkę wiskozometru. Usunąć musimy pęcherzyki powietrza, które pozostały na ściankach. Wkładamy kulkę i zamykamy rurkę korkiem zwracając uwagę na to, by wydrążenie w korku nie było całkowicie wypełnione cieczą. Nastawiamy odpowiednią temperaturę na termometrze kontaktowym i włączamy ultratermostat. Czas spadku kulki mierzymy stoperem, ponieważ czas ustalania się temperatury jest dość długi. Czas spadku kulki mierzymy do chwili, gdy uzyskamy przynajmniej trzy powtarzające się wyniki, dokładną wartość temperatury odczytujemy na termometrze znajdującym się w wiskozymetrze. Pomiary wykonujemy dla temperatury od pokojowej do 45[°C] w odstępach ok 5[°C]. Jako błąd pomiaru przyjmujemy błąd termometru DT.

3.2.Lepkość gazu.

Ruch cząsteczek gazu jest ruchem chaotycznym. Ponieważ w gazach można zaniedbać siły oddziaływania wzajemnego cząsteczek, ich ruch cieplny odbywa się ze stałą prędkością aż do chwili zderzenia z inną cząsteczką. W wyniku tego zderzenia zmienia się raptownie kierunek i wartość prędkości cząsteczki. Do opisu zachowania się cząsteczek można stsować jedynie prawa ststystyczne, co oznacza że musimy posługiwać się pojęciem średniej drogi swobodnej, średniej liczby zderzeń itp. Oznacza to też, że w każdym z możliwych kierunków porusza się średnio taka sama liczba cząsteczek. średnią prędkość poruszania się cząsteczek gazu można obliczyć stosując prawo rozkładu prędkości cząsteczek podane przez axwella. Odpowiedni rachunekprowadzi do wzoru: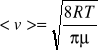
, gdzie T jest temperaturą gazu, µ jego masą molową, R uniwersalną stałą gazową. Jak widać średnia prędkość cząsteczek zależy od temperatury i rodzaju gazu.

W celu wyznaczenia średniej drogi swobodnej cząsteczek - sztywnej kulki (model),z prędkośćią <V> wystarczy obliczyć ilość zderzeń cząsteczek znajdujących się wewnątrz walca o wymiarach (2d x <v>t). Jeżeli koncentracja cząsteczek wynosi no to możemy zapisać, że: Z=no<v>td2. Koncentracje no możemy wyliczyć z równaia gazu doskonałego. Sumując otrynamy wzór na średnią drogę swobodną:
. Przekształcając to równanie możemy uzyskać wzór łączący <v> z <l>, który wykożystujemy do obliczń. Przekształcając powyższy wzór możemy także obliczyć średnicę cząsteczek powietrza: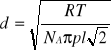
, który również uzależniamy od <v>.

Kożystając z kinetycznej teori gazów możemy stwierdzić, że wspólczynnik lepokści powietrza zależy jedynie od temperatury i rodzaju gazu. Zakładając że cząsteczki gazu (cienkie wartewki gazu) poruszają się prostopadle do powierzchni S (prostopadłej do ośi x) z prędkościami U1 i U2 wzglęgem współżędnej x, możemy obliczyć różnicę prędkości warstw 1 i 2, a co za tym idzie po przekształceniach współczynnik lepkości powietrza:
.

Celem ćwiczenia jest wyliczenie współczynnika lepkości powietrza. Dokonujemy tego na ukłądzie złożonym z butli z wodą, rurki kapilarnej oraz układu osuszającego. Wykożystując prawo Hagena-Poiseuille`a możemy badając zmianę ciśnienia uzależnić jego zmianę od różnicy poziomów cieczy manometrycznej h i gęstości cieczy.

3.Przebieg ćwiczenia.

3.1.Lepkość cieczy.

Sprawdzamy ustawienie wiskozymetru przy pomocy poziomicy. Zmieniając temperaturę cieczy przy pomocy ultratermostatu z termometrem kontaktowym w granicach od ok 45[°C] do temperatury pokojowej co ok 5[°C] mierzymy czas opadania kulki między skrajnymi położeniami obserwacyjnymi. Dla każdej temperatury pomiry powtarzamy trzykrotnie.

3.2.Lepkość gazu.

Sprawdzamy ustawienie przyżądów pomiarowych. Następnie ustawiamy szybkość wypływu wody odpowiadającą różnicy poziomu wody w manometrze ok 3 cm. Mierzymy 10-cio krotnie czas wypłynięcia z butli V=500 cm3 wody.

4.Opracowanie pomiarów.

4.1.Lepkość cieczy.

Dla każdej temperatury obliczamy współczynnik lepkości oleju parafinowego stosując wzór empiryczny: h=K(rk-ro)t, gdzie K=1.2018*10-6
- stała aparaturowa, rk=8150
- gęstość kulki, o - gęstość oleju (wg danych tablicowych), t - średnia wartość czasu opadania kulki.

Dla każdego h wyliczamy metodą różniczki zupełnej błąd Dh ze wzoru: Dh=K(rk-ro)Dt Następnie rysujemy wykres zależności temperaturowej współczynnika lepkości oleju parafinowego. Obliczamy kolejno ln|h|, oraz błąd. Dla kolejnych temperatur otrzymano:

lp.	T [°C]	ro		tśr [s]	h [kg/ms]	Dh [kg/ms]	ln|h| [kg/ms]	ln|Dh| [kg/ms]
1	24.0	876.1	0.00337	166.9	1.45900	0.00087	0.37775	-7.04223
2	26.0	874.6	0.00334	145.8	1.27481	0.00087	0.24280	-7.04202
3	29.0	872.5	0.00331	120.4	1.05303	0.00087	0.05167	-7.04173
4	34.0	868.9	0.00326	89.6	0.78404	0.00088	-0.24330	-7.04124
5	39.0	865.5	0.00321	75.5	0.65189	0.00086	-0.42788	-7.05459
6	42.0	863.3	0.00317	61.5	0.53857	0.00088	-0.61885	-7.04047
7	45.0	861.2	0.00314	51.5	0.45112	0.00088	-0.79601	-7.04018

Rysujemy wykres zależności
.

Metodą regresji liniowej obliczamy współczynniki A i B wzoru określającego temperaturową zależność współczynnika lepkości:
, gdzie k=1.38*10-23
- stała Boltzmana. Bląd wyliczenia h obliczano metodą różniczki zupełnej ze wzoru: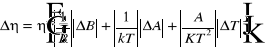
.

Obliczone współczynniki a i b wynoszą: a=5117.41433, b=-16.58734, błędy wynoszą: Da = 142.65379, Db = 0.46487 zatem otrzymujemy prostą zapisaną w postaci y=(a±Da)x + (b±Db) (1). Następnie logarytmując obustronnie wzór:
, otrzymujemy:
(2). Po porównaniu równania (2) z równaniem prostej (1) możemy obliczyć A i B, które odpowiednio zapisane A=a*k i B=exp(b), wynoszą: A=7.14483*10-20[J], B=6.25476*10-8[kg/ms]. Błędy wyznaczenia A i B liczone metodą różniczki zupełnej ze wzorów:
,
wynoszą: DA=1.96862*10-21[J], DB=2.90765*10-8[kg/ms]. Ostatecznie więc współczynnik lepkości cieczy wynosi: 1.09035*10-6±1.06259*10-7[kg/ms].

3.2.Lepkość gazu.

Obliczamy dla każdego z 10-ciu pomiarów wspołczynniki lepkości powietrza i błędy ich oliczenia ze wzorów:
, gdzie r=0.998*10-3
-gęstość wody,, g=9.81[m/s2]-przyspieszenie ziemskie, r=3.5*10-4[m]-promień rurki kapilarnej, l=0.078-długość rurki kapilarnej, v=5*10-4[m3]-objętość wody jaka została wypouszczona z zbiornika podczas ćwiczenia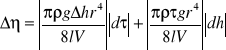
, gdzie dt=0.1[s], dh=0.001[m]. Następnie ze wzorów na średną ważoną:
i , obliczono średnią lepkość h.

Otrzymano następujące wartości:

lp.	h*10-7[kg/ms]	Dh*10-3[kg/ms]
1	206.368	0.457
2	196.116	0.401
3	203.779	0.433
4	191.367	0.422
5	195.716	0.45
6	188.882	0.428
7	198.823	0.453
8	202.063	0.434
9	188.882	0.421
10	194.562	0.489
śr.	195.462	0.141

Zatem ostatecznie lepkość powietrza wyniosła: h=195.462*10-7±0.141*10-7 [kg/ms].

Następnie obliczamy średnią drogę swobodną <l> i błąd jej wyliczenia D<l>, ze wzorów: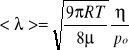
, gdzie po=727[mmHg], µ=28.83[g/mol], R=8.31[J/mol*K],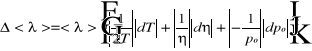
, gdzie dT=0.5[K], dpo=1[mmHg]. Otrzymano ostatecznie: <l>=4.636*10-8±0.010*10-8 [m].

Otrzymaną wartość wykożystujemy do obliczenia średnicy efektywnej cząsteczek powietrza ze wzoru: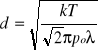
, gdzie k=1.38*10-23-stała Boltzmana, błąd wyliczenia Dd liczony ze jest wzoru: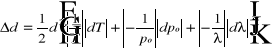
,. Otrzymano ostatedcznie:

d=5,196*10-10±0.014*10-10 [m].

5.Podsumowanie.

5.1.Lepkość cieczy.

W wyniku badania temperaturowej zależności współczynnika lepkości cieczy przy pomocy wiskozymetru Höpplera otrzymano następujące wartości liczbowe współczynników:

A=7.14483*10-20±1.96862*10-21[J],

B=6.25476*10-8±2.90765*10-8[kg/ms].

,które pozwoliły nam wyliczyć współczymmki lepkości cieczy:

h=1.09035*10-6±1.06259*10-7[kg/ms].

Otrzymana wartości obarczona jest błędem wynikłym na skutek niedokładności pomiaru temperatury i czasu oraz zanieczyszczenia rurki.

5.2.Lepkość gazu.

W wyniku badania temperaturowej zależności współczynnika lepkości gazu-powietrza otrzymano natępującą wartość liczbową wspólczynnika:

h=195.462*10-7±0.141*10-7 [kg/ms].

Wyliczono także średnią drogę swobodną:

<l>=4.636*10-8±0.010*10-8 [m].

Otrzymano taże następującą wartość średnicy efektywnej cząsteczki:

d=5.196*10-10±0.014*10-10 [m].

Wyniki jakie otrzymano porównywane w wartościami tablicowymi dla powietrza SUCHEGO są obarczone błędem, który pozwala wnioskować, że otrzymano wyniki z ma1łą dokładnością, której przyczyną może być: niedokładność pomiaru spuszczanego płynu z butli, nie dostatecze osuszanie powietrza.

---