Obligacje Podstawowe wiadomości o obligacji

Definicja obligacji Obligacja jest to instrument finansowy (papier wartościowy), w którym jedna strona, zwana emitentem obligacji, stwierdza, że jest dłużnikiem drugiej strony, zwanej obligatariuszem (jest to właściciel obligacji) i zobowiązuje się wobec niego do wykupu obligacji. Emisja obligacji jest formą zaciągnięcia kredytu. Kredytodawcą jest obligatariusz, czyli właściciel obligacji. Kredytobiorcą jest emitent obligacji. Cechy charakterystyczne obligacji Najważniejsze to: termin wykupu - jest to termin, po upływie którego emitent zobowiązany jest dokonać wykupu, tzn. zwrócić zaciągnięty kredyt właścicielowi obligacji; wartość (cena) nominalna - jest to wartość, którą emitent zwraca w dniu wykupu; cena emisyjna - jest to cena, po której obligacja jest sprzedawana w momencie emisji pierwszemu właścicielowi; oprocentowanie - określa wielkość odsetek od zaciągniętego kredytu; wyrażone jest w procentach wartości nominalnej; zwykle odsetki płacone są regularnie, np. co rok, co pół roku, co kwartał.

Przykład: Rozpatrzmy hipotetyczną obligację wyemitowaną w dniu 1.09.1995 z terminem wykupu 1.09.1997, której wartość nominalna wynosi 100, oprocentowanie 16%, przy czym odsetki płacone są co pół roku. Właściciel tej obligacji, który przetrzymał ją do terminu wykupu, otrzymał następujące dochody: - pół roku po zakupie (1.03.1996): 8 (odsetki półroczne); - rok po zakupie (1.09.1996): 8 (odsetki półroczne); - półtora roku po zakupie (1.03.1997): 8 (odsetki półroczne); - dwa lata po zakupie w momencie wykupu (1.09.1997): 8+100 (odsetki półroczne plus wartość nominalna). Oprocentowanie obligacji jest to cena kredytu, jaką płaci emitent obligacji właścicielowi obligacji.

Podstawowe rodzaje obligacji

Podział obligacji ze względu na różne kryteria Kryterium emitenta Najważniejsze rodzaje obligacji: obligacje skarbowe, emitowane przez Skarb Państwa; obligacje przedsiębiorstw; obligacje komunalne (emitowane przez gminy, związki gmin). Kryterium oprocentowania Wyróżnia się: obligacje o stałym oprocentowaniu; obligacje o zmiennym oprocentowaniu; obligacje zerokuponowe. Obligacje o stałym oprocentowaniu Obligacje o stałym oprocentowaniu to takie obligacje, których oprocentowanie jest znane i nie zmienia się przez cały czas do terminu wykupu. Strukturę przepływów pieniężnych dla obligacji o stałym oprocentowaniu przedstawia poniższy przykład.

Przykład: Obligacja o stałym oprocentowaniu, z terminem wykupu za 3 lata, wartość nominalna 100, cena emisyjna po jakiej emitent oferuje obligacje 98, oprocentowanie 10%, odsetki płacone co pół roku.

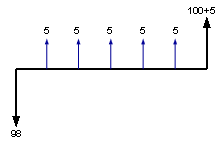
Struktura przepływów pieniężnych dla tej obligacji

Obligacje o zmiennym oprocentowaniu
Obligacje o zmiennym oprocentowaniu to takie obligacje, których oprocentowanie zmienia się w okresach odpowiadających płatnościom odsetek. Oprocentowanie to zależy od ustalonego wskaźnika, którym może być np. stopa rentowności bonów skarbowych (w okresie poprzedzającym płatność odsetek). Strukturę przepływów pieniężnych dla obligacji o zmiennym oprocentowaniu przedstawia poniższy przykład.

Przykład:
Obligacja o zmiennym oprocentowaniu, z terminem wykupu za 3 lata, wartość nominalna 100, cena emisyjna 103, odsetki płacone co pół roku. Oprocentowanie w skali rocznej jest o 1 punkt procentowy wyższe od stopy rentowności 26-tygodniowych bonów skarbowych. W kolejnych okresach (było ich sześć) poprzedzających płatności odsetek, roczna stopa wynosiła: 19%, 20%, 21%, 17%, 17%, 21%. Odsetki zatem, liczone dla okresów półrocznych, po uwzględnieniu podwyżki o 1 punkt procentowy, wynoszą kolejno: 10, 10, 5, 11, 9, 9, 11.

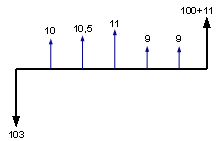
Struktura przepływów pieniężnych dla tej obligacji.

Do obligacji o zmiennym oprocentowaniu można (upraszczając) zaliczyć również obligacje indeksowane, których oprocentowanie zależy od stopy inflacji.

Obligacje zerokuponowe
Obligacje zerokuponowe (inaczej: obligacje z kuponem zerowym) to takie obligacje, od których nie są płacone odsetki, ale cena obligacji jest zawsze niższa niż wartość nominalna. Strukturę przepływów pieniężnych dla obligacji zerokuponowej przedstawia poniższy przykład.

Przykład:
Obligacja zerokuponowa, z terminem wykupu za 3 lata, wartość nominalna 100, cena emisyjna 93.

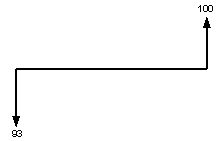
Struktura przepływów pieniężnych dla tej obligacji

Bardziej złożone obligacje
Ostatnio na świecie pojawia się wiele bardziej złożonych rodzajów obligacji, np.:

• obligacje zamienne - w tym przypadku właściciel ma prawo do zamiany obligacji na inny instrument finansowy, np. zamiana obligacji pewnej spółki na jej akcje;

• obligacje z opcją wykupu na żądanie emitenta (call) - emitent ma prawo zażądać wykupu przed ustalonym terminem;

• obligacje z opcją sprzedaży na żądanie właściciela (put) - właściciel ma prawo zażądać wykupu przed ustalonym terminem.

Obligacje mogą być sprzedawane w innym kraju niż kraj emitenta. Nazywa się je wówczas euroobligacjami.

Obligacje w Polsce

Obligacje skarbowe Obecnie (sierpień 99) w Polsce dostępnych jest pięć rodzajów obligacji skarbowych: jednoroczne, dwuletnie, trzyletnie, pięcioletnie, dziesięcioletnie. Obligacje jednoroczne Są to obligacje indeksowane. Termin wykupu tych obligacji wynosi 1 rok, wartość nominalna - 100 PLN. Odsetki płacone są po roku w momencie wykupu. Oprocentowanie tych obligacji zależy od stopy inflacji. Przykład: Stopa inflacji wynosiła 18%. Inwestor kupił obligację roczną płacąc za nią 97 PLN. Po roku otrzymał (oprocentowanie na poziomie stopy inflacji) 118 PLN, stopa dochodu inwestora w skali roku wyniosła: (118- 97) / 97 =21,65%. Ogólny wzór na stopę dochodu polskiej obligacji indeksowanej jest następujący: r = [(100(1+i+L)-P)/P] x 100% gdzie: r - stopa dochodu polskiej jednorocznej obligacji indeksowanej, i - stopa inflacji, L - nadwyżka oprocentowania nad stopę inflacji P - cena zakupu obligacji.

Obligacje dwuletnie Są to obligacje o stałym oprocentowaniu. Termin wykupu tych obligacji wynosi 2 lata, wartość nominalna -1000 PLN. Odsetki płacone są co rok. Obligacje trzyletnie Są to obligacje o zmiennym oprocentowaniu. Termin wykupu tych obligacji wynosi 3 lata, wartość nominalna - 100 PLN. Odsetki płacone są co kwartał. Oprocentowanie tych obligacji zależy od średniej stopy rentowności 13-tygodniowych bonów skarbowych. Obligacje pięcioletnie Są to obligacje o stałym oprocentowaniu. Termin wykupu tych obligacji wynosi 5 lat, wartość nominalna -1000 PLN. Odsetki płacone są co rok. Obligacje dziesięcioletnie Są to obligacje o zmiennym oprocentowaniu. Termin wykupu tych obligacji wynosi 10 lat, wartość nominalna - 1000 PLN. Odsetki płacone są co rok. Oprocentowanie tych obligacji zależy od średniej stopy rentowności 52-tygodniowych bonów skarbowych. Inne rodzaje obligacji Oprócz obligacji skarbowych w Polsce zaczyna się emitować obligacje gminne (komunalne). Wiele spółek publicznych wyemitowało także obligacje zamienne na akcje. W takim wypadku akcje te muszą być dopuszczone do publicznego obrotu. Akty prawne W Polsce emisję i obrót obligacjami regulują różne akty prawne. Najważniejsze to: Ustawa o obligacjach, Ustawa o publicznym obrocie papierami wartościowymi, zarządzenia Ministra Finansów o emisji obligacji skarbowych. Obrót obligacjami Obligacjami obraca się na rynku pierwotnym i wtórnym. O rynku pierwotnym obligacji mówimy wtedy, gdy obligacje są sprzedawane pierwszemu właścicielowi. Następnie obligacje trafiają na rynek wtórny, gdzie odbywa się właściwy nimi obrót. Rynek pierwotny obligacji skarbowych w Polsce to przetargi obligacji lub oferta sprzedaży za pośrednictwem biur maklerskich. Rynek wtórny obligacji w Polsce to Giełda Papierów Wartościowych w Warszawie lub Centralna Tabela Ofert (CeTO).

Cena i wartość obligacji

	Cena obligacji na rynku Cena obligacji na rynku jest sumą dwóch składników: tzw. ceny czystej, którą jest kurs obligacji, wyrażony w procentach wartości nominalnej; odsetek, które narosły od momentu ostatniej płatności. Oczywiście w przypadku obligacji zerokuponowej odsetki równe są zeru. Przykład: Rozpatrzmy hipotetyczną obligację wyemitowaną w dniu 1.06.1996, której termin wykupu przypada w dniu 1.06.1998. Wartość nominalna tej obligacji wynosi 100, oprocentowanie 12%, odsetki płacone są co pół roku. Kurs obligacji na giełdzie w dniu 1.09.1997 tj. 1/4 roku od ostatniej płatności wynosi 95. Obliczmy cenę obligacji. Pierwszy składnik jest równy: 95 =0,95 x 100 (kurs obligacji w procentach razy wartość nominalna). Drugi składnik jest równy: 3 =0,12 x (1/4) x 100 (oprocentowanie obligacji w skali rocznej razy część roku, która upłynęła od ostatniej płatności razy wartość nominalna). Cena obligacji wynosi 95 + 3 =98 W powyższym przykładzie poczyniliśmy pewne uproszczenie, przyjmując proporcjonalny przyrost odsetek od ostatniej płatności (upłynęły 3 miesiące, co stanowi czwartą część roku). W rzeczywistości w różnych krajach dla różnych obligacji stosowane są różne sposoby naliczania odsetek; często pod uwagę jest brana rzeczywista liczba dni, które upłynęły od ostatniej płatności. W Polsce sposoby naliczania odsetek podawane są w konkretnych zarządzeniach.
Wartość obligacji Wartość obligacji na rynku (a zatem jej cena) kształtuje się w wyniku popytu i podaży, które z kolei zależą od różnych czynników. Najważniejszym czynnikiem kształtującym wartość obligacji jest poziom stóp procentowych. Inwestorzy często dokonują wyceny obligacji. Wycena obligacji polega na określeniu tzw. sprawiedliwej ceny obligacji, która powinna odzwierciedlać wartość obligacji. Najczęściej stosowaną metodą przy wycenie obligacji Jest metoda dochodowa, inaczej metoda zdyskontowanych przepływów pieniężnych. Według tej metody: Wartość obligacji jest sumą dochodów, które inwestor otrzyma w okresie posiadania obligacji, przy czym dochody te są zdyskontowane, czyli "przeliczone na moment dokonywania wyceny". Stosuje się tu wzór: gdzie: P - wartość obligacji, otrzymana w wyniku wyceny, n - liczba okresów posiadania obligacji, Ct - dochód z tytułu posiadania obligacji, uzyskany w tym okresie posiadania obligacji, r - tzw. wymagana stopa dochodu, określona w skali okresu płatności odsetek, jeśli np. odsetki płacone są co pół roku, to jest to stopa półroczna. Wymagana stopa dochodu określana jest przez inwestora na podstawie stóp dochodu obligacji podobnego typu jak wyceniana obligacja. Informacje na ten temat podawane są w dziennikach finansowych. Wartość obligacji a cena obligacji Inwestor porównuje wartość obligacji uzyskaną w wyniku wyceny z ceną obligacji na rynku. Możliwe są tu trzy przypadki: wartość wyceniona jest wyższa od ceny rynkowej - inwestor ocenia, że obligacja jest warta więcej niż kosztuje na rynku - jest to tzw. niedowartościowanie obligacji; w takiej sytuacji należałoby kupić obligację; wartość wyceniona jest niższa od ceny rynkowej - inwestor ocenia, że obligacja jest warta mniej niż kosztuje na rynku - jest to tzw. przewartościowanie obligacji; w takiej sytuacji należałoby sprzedać obligację; wartość wyceniona jest równa cenie rynkowej - inwestor ocenia, że obligacja jest warta dokładnie tyle, ile kosztuje na rynku. Wartość obligacji o stałym oprocentowaniu Wzór na wartość obligacji można stosować również dla obligacji o stałym oprocentowaniu. Ilustrują to dwa przykłady. Przykład 1: Rozpatrzmy hipotetyczną obligację o terminie wykupu przypadającym za dwa lata. Wartość nominalna tej obligacji wynosi 100, oprocentowanie 12%, odsetki płacone są co rok. Wymagana stopa dochodu określona przez inwestora wynosi 14%. Po podstawieniu do wzoru otrzymujemy: P = 12/(1+0,14) + 112/(1+0,14)^2= 96,71 Przykład 2: Rozpatrzmy podobną obligację jak w poprzednim przykładzie, z tym że odsetki płacone są co pół roku (a nie co rok). Mamy tu zatem do czynienia z okresami półrocznymi. Wymagana stopa dochodu określona przez inwestora jest tutaj stopą półroczną, a zatem wynosi 0,14:2 = 7%. Po podstawieniu do wzoru otrzymujemy: Wartość obligacji zerokuponowej Najprościej dokonuje się wyceny w przypadku obligacji zerokuponowej. Ilustruje to poniższy przykład. Przykład: Rozpatrzmy hipotetyczną obligację zerokuponową o terminie wykupu przypadającym za dwa lata. Wartość nominalna obligacji wynosi 100, a wymagana stopa dochodu określona przez inwestora wynosi 11%. 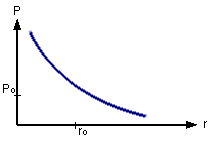Po podstawieniu do wzoru na wartość obligacji: P = 100/(1+0,11)^2= 81,16 Wartość obligacji a stopy procentowe Podstawowym czynnikiem, który decyduje o wartości, a w konsekwencji również o cenie obligacji, jest stopa procentowa. Zmiany stóp procentowych powodują zmiany wymaganych stóp dochodu inwestorów, co z kolei powoduje zmianę wartości obligacji. Ilustruje to następująca reguła: Wzrost stóp procentowych powoduje spadek wartości obligacji o stałym oprocentowaniu i obligacji zerokuponowych, a spadek stóp procentowych powoduje wzrost wartości obligacji o stałym oprocentowaniu i obligacji zerokuponowych.

Na wykresie na osi odciętych zaznaczony jest poziom stóp procentowych, a na osi rzędnych wartość obligacji. Jak widać, zmiany wartości obligacji w wyniku zmian stóp procentowych nie są proporcjonalne.

Stopa dochodu z obligacji

Dochód z obligacji Dochód z obligacji określony jest poprzez stopę dochodu obligacji, nazywaną również stopą dochodu w okresie do wykupu obligacji. Zwykle oznacza się ją przez YTM (ang. Yield To Maturity). Oblicza się ją na podstawie Stopa YTM określa, jaką stopę dochodu (w skali roku) uzyska inwestor, który kupi obligację po cenie P, przetrzyma ją do terminu wykupu, a także będzie reinwestował odsetki (na okres do terminu wykupu). Określanie stopy dochodu obligacji - przykłady Najłatwiej określa się stopę dochodu obligacji zerokuponowej. Przykład: Dana jest hipotetyczna obligacja zerokuponowa z terminem wykupu za dwa lata. Wartość nominalna obligacji wynosi 100. Obligacja została kupiona za 85. Po podstawieniu do wzoru (2) otrzymujemy: 85 = 100/(1 + YTM)^2 Po rozwiązaniu powyższego równania otrzymujemy: YTM = 8,47%

Trudniej określa się stopę dochodu obligacji o stałym oprocentowaniu. Przykład: Dana jest hipotetyczna obligacja z terminem wykupu za 3 lata. Wartość nominalna obligacji wynosi 100, oprocentowanie - 15%, odsetki płacone są co rok. Obligacja została kupiona za 102. Po podstawieniu do wzoru otrzymujemy: 102 = 15/(1 + YTM) + 15/(1 + YTM)^2+ 115/(1 + YTM0,14)^3 Do rozwiązania powyższego równania niezbędne jest zastosowanie komputera bądź kalkulatora finansowego. Wynik jest następujący: YTM = 14,14% Na świecie stopy dochodu najważniejszych rodzajów obligacji są podawane w środkach masowego przekazu.

Ryzyko inwestycji w obligacje

Gdyby inwestor zamierzał sprzedać obligację przed terminem wykupu, trudniej byłoby określić stopę dochodu, ponieważ inwestor nie znałby dokładnie ceny sprzedaży, a zatem nie mógłby dokładnie określić dochodu, który uzyska. Oznacza to, że istnieje ryzyko inwestycji w obligacje. Podstawowe rodzaje ryzyka inwestycji w obligacje Generalnie można powiedzieć, że obligacje są instrumentami finansowymi o mniejszym ryzyku niż akcje, jednak różne rodzaje obligacji charakteryzują się różnym poziomem ryzyka. Jest kilka rodzajów ryzyka inwestycji w obligacje. Do najważniejszych, które powinien brać pod uwagę inwestor, należy zaliczyć: ryzyko niedotrzymania warunków (w tym ryzyko bankructwa); ryzyko stopy procentowej. Ryzyko niedotrzymania warunków Ryzyko niedotrzymania warunków jest to ryzyko wynikające z faktu, że emitent (a więc zaciągający kredyt) może nie zwrócić kwoty równej wartości nominalnej lub nie zapłacić odsetek (lub jedno i drugie). Obligacje skarbowe są w zasadzie wolne od tego ryzyka, gdyż mamy prawo oczekiwać, że Skarb Państwa jest wypłacalnym dłużnikiem. Największym ryzykiem niedotrzymania warunków charakteryzują się obligacje przedsiębiorstw. Do oceny ryzyka niedotrzymania warunków służy tzw. rating obligacji. Jest on tworzony przez wyspecjalizowane instytucje i polega na zakwalifikowaniu obligacji do klas o różnym poziomie ryzyka niedotrzymania warunków.

Im wyższe ryzyko niedotrzymania warunków, tym wyższe powinno być oprocentowanie obligacji. Im wyższe ryzyko niedotrzymania warunków, tym wyższa stopa dochodu obligacji. Ryzyko stopy procentowej Podstawowym przejawem ryzyka stopy procentowej jest możliwość zmiany wartości (a zatem również ceny) obligacji w sytuacji zmian stóp procentowych na rynku. Nazywa się to również ryzykiem zmiany wartości. Im bardziej wartość obligacji reaguje na zmiany stóp procentowych, tym większe jest ryzyko stopy procentowej. Pozytywny przejaw ryzyka stopy procentowej występuje w przypadku spadku stóp procentowych, gdyż wtedy rośnie wartość obligacji. Negatywny przejaw ryzyka stopy procentowej występuje w przypadku wzrostu stóp procentowych, gdyż wtedy spada wartość obligacji. Im wyższe oprocentowanie obligacji, tym mniejsze ryzyko zmiany wartości obligacji. Im krótszy okres do terminu wykupu obligacji, tym mniejsze ryzyko zmiany wartości obligacji. Płynność obligacji Płynność, tzn. możliwość szybkiej sprzedaży obligacji po oczekiwanej cenie, różni się dla różnych rodzajów obligacji. Najbardziej płynne są obligacje skarbowe. Małą płynnością charakteryzują się obligacje komunalne niewielkich miast i gmin oraz obligacje przedsiębiorstw mało znanych, działających na małym terenie. Konkluzja Inwestycje w obligacje należy preferować, gdy inwestorowi zależy na ograniczaniu ryzyka. Należy wówczas inwestować w obligacje skarbowe i trzymać je do terminu wykupu. Inną zasadą jest inwestowanie w obligacje o długości okresu do terminu wykupu zbliżonej do horyzontu inwestycyjnego. Jeśli np. inwestor spodziewa się większych wydatków za dwa lata, wówczas powinien inwestować w dwuletnie obligacje skarbowe. Z kolei chęć zwiększania stopy dochodu prowadzi do konieczności inwestowania w obligacje o dużym poziomie ryzyka.

---