ZACHODNIOPOMORSKI UNIWERSYTET TECHNOLOGICZNY W SZCZECINIE
SPRAWOZDANIE Z LABORATORIUM STATYSTYKI MATEMATYCZNEJ
ĆW. NR: 3	TEMAT: BADANIE ZGODNOŚCI ROZKŁADU ZMIENNEJ LOSOWEJ Z ROZKŁADEM TEORETYCZNYM
DATA WYK. ĆW. 07.12.2011		IMIĘ I NAZWISKO STUDENTA: Mateusz Krawczyk		OCENA:		PODPIS:	GRUPA: T1-21
PROWADZĄCY ĆWICZENIE:			ROK AKADEMICKI: 2011/2012		SEMESTR: 3

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się ze sposobami weryfikacji hipotezy o zgodności rozkładu zmiennej losowej z proponowanym rozkładem teoretycznym (modelem rozkładu).

2. Podstawy teoretyczne

Wielokrotnie w analizie statystycznej zakładamy, że zmienne losowe ( badane cechy) mają pewne rozkłady, np. normalne, Poissona czy inne. Powstaje zatem pytanie, czy takie założenie jest zgodne z rzeczywistością. Aby to sprawdzić, dokonuje się obserwacji badanej cechy (pobiera próbkę losowa) i porównuje rozkład obserwacji zawartych w próbie z pewnym teoretycznym rozkładem, który to rozkład można uważać za proponowaną hipotezę zerową. Hipoteza zerowa może być postawiona w różnej postaci, np.: H₀: zmienna losowa X ma rozkład normalny o parametrach µ=5 i σ=0,5 lub H₀: zmienna losowa X jest zmienną Poissona o parametrze λ=5 lub przy braku konkretnej wartości parametrów H₀: zmienna losowa X podlega rozkładowi wykładniczemu. Hipoteza alternatywna określająca, że zmienna nie jest taka, jak żąda tego hipoteza zerowa H₀, jest najczęściej bardzo złożona. Np. jeżeli X nie jest zmienną losową o rozkładzie N(5;0,5) to może mieć rozkład N(5;0,3) lub N(10;0,5) lub N(15;0,4) lub może w ogóle nie mieć rozkładu normalnego, może mieć rozkład logarytmo-normalny lub gamma, lub dowolny z nieskończenie wielu nazywanych lub bez nazwy, ciągłych, dyskretnych lub mieszanych różnorodnych rozkładów.

1. Porównanie kształtów histogramów

Najprostszym sposobem oceny zgodności rozkładu obserwacji próby z rozkładem hipotetycznym jest wizualne porównanie histogramów.

2. Porównanie histogramu częstości z funkcją gęstości

Porównując kształt histogramu częstości danych z funkcją gęstości rozkładu hipotetycznego należy tak wybrać liczbę klas histogramu aby wypośrodkować między większą niejednoznacznością a większą zmiennością. Więc jeżeli uzasadnia się adekwatność swojego rozkładu na podstawie wizualnego porównania, to trzeba pamiętać, że jeżeli przyjmie się małą liczbę klas to inne rozkłady będą miały też prawie identyczną zgodność, a jeżeli wybierze się zbyt dużą liczbę klas to duże podobieństwo kształtów będzie mało prawdopodobne.

3. Porównanie histogramu skumulowanej częstości z dystrybuantą

Zamiast porównywać zaobserwowany histogram częstości danych z funkcją gęstości można porównywać histogram skumulowanej częstości (dystrybuantę empiryczną) z wykresem dystrybuanty. Porównanie kształtu histogramu skumulowanej częstości z dystrybuantą ma wyraźną przewagę nad porównaniem histogramu częstości z funkcją gęstości. W tym przypadku znacznie zmniejsza się niejednoznaczność i zmienność histogramu związana z koniecznością grupowania danych.

4. Testy zgodności

Bardziej obiektywne są oceny ilościowe zgodności na podstawie testów statystycznych. Opracowano wiele testów, które dzielą się na dwie grupy. Do pierwszej należą testy, które mogą być stosowane dla dowolnego hipotetycznego rozkładu. Do drugiej grupy należą testy bardziej specjalistyczne służące do badania zgodności z konkretnym rozkładem hipotetycznym.

5. Test Chi-kwadrat

Test Chi-kwadrat przeprowadza się w następujący sposób. Dokonuje się n obserwacji zmiennej losowej X. Otrzymany zakres zmienności zaobserwowanych wartości dzieli się na k klas. Oblicza się liczbę obserwacje n_i należących do każdej klasy. Jeżeli hipoteza zerowa jest prawdziwa, można oczekiwać, że liczba obserwacji w każdej klasie powinna wynosić np_i.

6. Test Kołmogorowa

Przewaga testu Kołmogorowa nad testem Chi-kwadrat polega na tym, że nie wymaga on łączenia danych w grupy i porównywania oddzielnych klas, ale porównuje wszystkie dane w niezmienionej postaci i dzięki temu jest niewrażliwy na działanie skrajnych, małolicznych klas.

7. Test normalności Lillieforsa

Test ten służy do weryfikacji hipotezy zerowej, że zmienna losowa X ma rozkład normalny N(µ,σ). Jeżeli parametry tego rozkładu są znane, to weryfikacji hipotezy zerowej można stosować opisany wcześniej test Kołmogorowa. Jeżeli zaś parametry te nie są znane, to należy stosować zmodyfikowany test Kołmogorowa, znany pod nazwą testu Lillieforsa. Statystyka tego testu jest taka sama jak testu Kołmogorowa, z tym że do wyznaczenia hipotetycznej dystrybuanty F(X) wykorzystuje się oceny X i s² nieznanych parametrów rozkładu normalnego.

8. Test normalności Shapiro-Wilka

Drugim testem, który weryfikuje hipotezę o normalności rozkładu zmiennej losowej w przypadku nieznanych parametrów rozkładu hipotetycznego jest test Shapiro-Wilka. W zależności od przyjętego poziomu istotności alfa i liczebności próbki n należy odczytać z tablic wartości krytycznych testu Shapiro-Wilka wartość krytyczną W_α,n . Jeżeli w < W_α,n to hipotezę o normalności rozkładu zmiennej losowej X należy odrzucić.

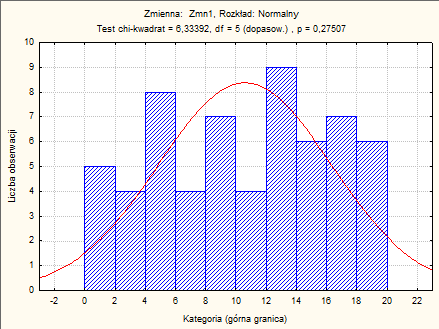
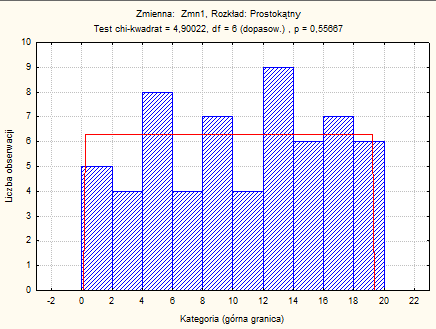
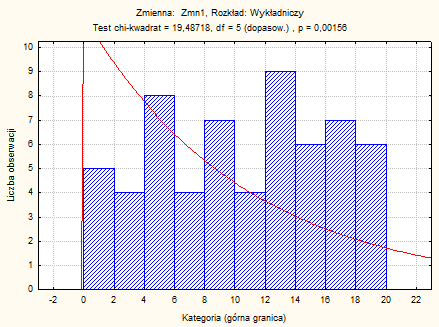
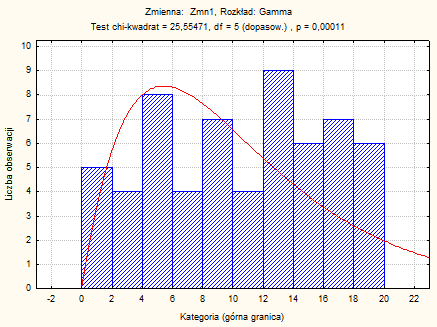
Wnioski:

Otrzymano wartości statystyk testowych maks D oraz W dla testów Lillieforsa i Sharpiro-Wilka. Mamy też podane prawdopodobieństwa p nie odrzucania hipotezy zerowej, gdy jest ona prawdziwa. Ponieważ wartości tych prawdopodobieństw przekraczają wartość przyjętego poziomu istotności α=0,05, nie ma więc podstaw do odrzucenia hipotezy zerowej.

---