SZKOŁA GŁOWNA SŁUŻBY POŻARNICZEJ |
|||
KATEDRA TECHNIKI POŻARNICZEJ |
LABORATORIUM HYDROMECHANIKI |
||
Ćwiczenie nr 2
Temat: Określenie wydatku za pomocą pomiaru prędkości przepływu osiowo - symetrycznego |
Pluton 1 |
wykonał:
st. asp. Piotr Kozłowski |
|
|
Grupa: A |
|
|
Prowadzący: kpt. mgr inż. E. Pawlak
|
Data wykonania: 17.02.2002r. |
Data złożenia:
03.03.2002r |
Ocena:
|
CEL ĆWICZENIA :
Celem ćwiczenia jest określenie wydatku za pośrednictwem pomiaru rozkładu
prędkości dla przepływu osiowo symetrycznego oraz porównanie wydatku zmierzonego przy pomocy kryzy z wydatkiem rzeczywistym .
Wstęp teoretyczny do ćwiczenia
Gaz doskonały ma następujące właściwości :
Posiada trwałość stanu gazowego .
Ma niezbędną budowę chemiczną i cząsteczkową .
Posiada stałe ciepło właściwe .
Nie ma zdolności przeniesienia naprężeń stycznych .
Stan fizyczny gazu doskonałego określa wzór :
p · v = R · T
p - ciśnienie
v - objętość właściwa·
R - indywidualna stała gazowa
T - temperatura gazu ,
Ciśnienie w poruszającym się płynie .
W poruszającym się strumieniu gazu podobnie jak w cieczy wyodrębniamy ciśnienia :
Ciśnienie statyczne
Ciśnienie dynamiczne
Ciśnienie całkowite
Pc = ps + pd
Ciśnienie statyczne jest to ciśnienie wskazywane przez przyrząd poruszający się w strumieniu płynu z taką samą prędkością i w tym samym kierunku , w którym porusza się płyn , czyli prędkość względna przyrządu i płynu równa się
zero .
Ciśnienie dynamiczne związane jest z ruchem płynu .
Równanie Bernoullego
ၲ · x · v2
pd = ----------------
2
ၲ - gęstość
v - prędkość przepływu
pd - ciśnienie dynamiczne
Schemat stanowiska pomiarowego:
Stanowisko pomiarowe składa się z pomiarowej rury poziomej, pionowej rury z kryzą. Przepływ powietrza jest wymuszony wentylatorem odśrodkowym, napędzanym silnikiem elektrycznym. Regulację wydatku uzyskuje się poprzez zmianę położenia regulatora wydatku.
Ciśnienie dynamiczne jest mierzone rurką Prandtla, która jest przesuwana w płaszczyźnie prostopadłej do kierunku przepływu. Do kontroli ustawienia rurki pomiarowej względem ścianki rury służy odpowiednia podziałka. Mikromanometr jest połączony różnicowo z rurką Prandtla. Ciśnienie różnicowe na kryzie jest wskazywane przez drugi mikromanometr.
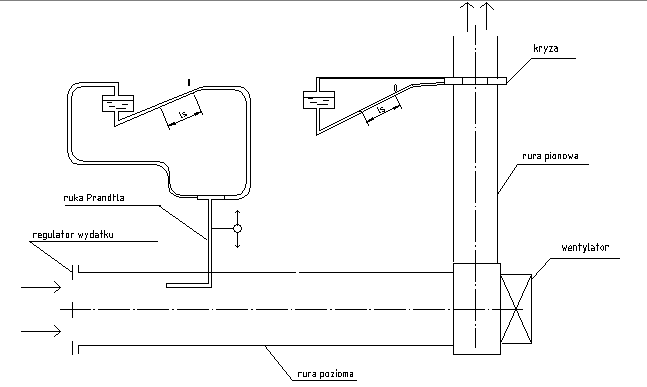
Tabela pomiarów:
Lp. |
Położenie rurki Prandtla
R [mm] |
Wychylenie się cieczy w manometrze Lp [mm] |
Wychylenie się cieczy na kryzie
Lk [mm] |
1 |
48 |
144 |
85 |
2 |
45 |
144 |
85 |
3 |
40 |
145 |
84 |
4 |
35 |
147 |
86 |
5 |
30 |
145 |
84 |
6 |
25 |
145 |
84 |
7 |
20 |
142 |
85 |
8 |
15 |
132 |
84 |
9 |
12 |
122 |
85 |
10 |
10 |
130 |
85 |
11 |
8 |
112 |
85 |
12 |
6 |
105 |
85 |
13 |
4 |
100 |
85 |
14 |
2 |
80 |
85 |
Tabela wyników:
Lp. |
Obliczone ciśnienie dynamiczne
Pd [Pa] |
Obliczona prędkość powietrza
Vpow(R) [m/s] |
Obliczony iloczyn
R·Vpow(R) [m2/s] |
1 |
22,03 |
5,82 |
0,279 |
2 |
22,03 |
5,82 |
0,262 |
3 |
22,19 |
5,84 |
0,234 |
4 |
22,49 |
5,88 |
0,206 |
5 |
22,19 |
5,84 |
0,175 |
6 |
22,19 |
5,84 |
0,146 |
7 |
21,73 |
5,78 |
0,116 |
8 |
20,20 |
5,57 |
0,083 |
9 |
18,67 |
5,35 |
0,064 |
10 |
19,89 |
5,33 |
0,055 |
11 |
18,36 |
5,31 |
0,042 |
12 |
16,06 |
4,97 |
0,030 |
13 |
15,30 |
4,85 |
0,019 |
14 |
12,24 |
4,33 |
0,009 |
Przykładowe obliczenia:
Obliczanie ciśnienia dynamicznego:
Dane: Obliczenia:
Lp = 0,142 [m] pd =Lp · np · ρcm · g
np. = 1/50 = 0,02 pd = 0,142 · 0,02 · 780 · 9,81
ρcm = 780 [kg/m3] pd = 21,73[Pa]
g = 9,81 [m/s2]
Dane: Obliczenia:
Lp = 0,105 [m] pd =Lp · np · ρcm · g
np. = 1/50 = 0,02 pd = 0,105 · 0,02 · 780 · 9,81
ρcm = 780 [kg/m3 ] pd = 16,06 [Pa]
g = 9,81 [m/s2]
Obliczanie prędkości powietrza:
Dane: Obliczenia:
pd = 22,49 [Pa] Vpow(R) = √(2pd/ ρpow)
ρpow = 1,3 [kg/m3] Vpow(R) = 5,88 [m/s]
Dane: Obliczenia:
pd = 16,06 [Pa] Vpow(R) = √(2pd/ ρpow)
ρpow = 1,3 [kg/m3] Vpow(R) = 4,97 [m/s]
Obliczanie iloczynu:
Dane: Obliczenia:
R = 0,035 [m] R·Vpow(R) = 0,206 [m2/s]
Vpow(R) = 5,88 [m/s]
Dane: Obliczenia:
R = 0,006 [m] R·Vpow(R) = 0,030 [m2/s]
Vpow(R) = 4,97 [m/s]
Obliczenie pola trójkąta z wykresu:
Dane: Obliczenia:
d = 24 [cm] F = 1/2 · d · h
h = 14,5 [cm] F = 174 [cm2]
Obliczenie pola trójkąta z wykresu:
Dane: Obliczenia:
d = 24 [cm] F = 1/2 · d · h
h = 14,5 [cm] F = 174 [cm2]
Obliczanie wydatku rzeczywistego:
Obliczenie κ z wykresu:
x → 1 cm = 0,002 [m] κ = x · y = 0,00004 [m3/s/cm2]
y → 1 cm = 0,02 [m2/s]
Dane: Obliczenie:
Π = 3,14 Qrz = 2 · Π · F · κ
F = 174 [cm2] Qrz = 0,0437 [m3/s]
κ = 0,00004 [m3/s/cm2]
7. Obliczenia dla kryzy:
obliczenie średniego wychylenia na kryzie:
Lśr = 85 [mm]
obliczenie ciśnienia różnicowego na kryzie:
Dane: Obliczenia:
Lkśr = 0,085 [m] p = Lkśr · nk · ρcm · g
nk = 1/10 = 0,1 p = 65,0 [Pa]
ρcm = 780 [kg/m3]
g = 9,81 [m/s2]
obliczenie modułu kryzy:
Dane: Obliczenie:
dk = 0,0756 [m] m = ( dk/dr)2
dr = 0,096 [m] m = 0,62
8.Obliczanie wydatku teoretycznego:
Dane: Obliczenie:
m = 0,62 Qt = [1/√(1-m2)]·[(Πdk2)/4]·[√(2p/ ρpow)]
Π = 3,14 Qt = 0,057 [m3/s]
dk = 0,0756 [m]
p = 65,0 [Pa]
ρpow 1,3 [kg/m3]
9.Obliczenie współczynnika wydatku kryzy:
Dane: Obliczenie:
Qrz = 0,0437 [m3/s] α = Qrz/Qt
Qt = 0,057 [m3/s] α = 0,76
10.Wykresy znajdują się na końcu sprawozdania.
11.Wnioski:
Po przeprowadzeniu ćwiczenia za pośrednictwem pomiaru rozkładu prędkości dla przepływu osiowo symetrycznego oraz porównując wyniki obliczeń wydatku objętościowego (rzeczywisty ) i wydatku zmierzony przy pomocy kryzy ( teoretyczny ) można stwierdzić , że wydatek rzeczywisty jest mniejszy od wydatku teoretycznego (współczynnik ၡ = 0,76 ) .Jest mniejszy, ponieważ wpisaliśmy uproszczenie przez założenie jednorodnego rozkładu prędkości oraz nie uwzględniliśmy strat ciśnienia na kryzie. Jest wiele metod badania wydatku, ale dzięki tej metodzie możemy zapoznać się z zasadami i metodami działania urządzeń pomiarowych w tym ćwiczeniu.
12. Przeliczanie jednostek :
30 MPa = 300at = 300 bar = 300 kG/cm2 = 3000 msw = 3 x 105 hPa = 3 x 106 kG / m2=3 x 106 kG / m2 = 3 x 107 Pa = 3 x 107 N/m2 = 220800 mmHg = 220800 Tr
Wyszukiwarka
Podobne podstrony:
Przepływ osiowo symetryczn4, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
osiowo symetryczny3, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
Sciąga przepływ, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
12 jarek, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
charakterystyk pomp wirowych odśrodkowych, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
ćw 9, SGSP, SGSP, cz.1, hydromechanika, hydra
cwiczenie 9 hydra brzoza krzywusek, SGSP, SGSP, cz.1, hydromechanika, hydra
zadania hydra, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
Hyromechanika lab, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
tabelka wynikowa do ćw 9, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
HYDRA ściąga, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
C11, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika, instrukcje stare
hydra tabelka, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
c12, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika, instrukcje stare
HYDRA ściąga2, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
PAGÓREK, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
Hydromechanika, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
charak pomp wirowych, SGSP, SGSP, cz.1, hydromechanika, Hydromechanika
więcej podobnych podstron