SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ
KATEDRA TECHNIKI POŻARNICZEJ		LABORATORIUM HYDROMECHANIKI
Ćwiczenie nr: 2 Temat: Określanie wydatku za pośrednictwem pomiaru rozkładu prędkości w przepływie osiowo - symetrycznym.	Pluton: 1	Imię i nazwisko: asp. Stanisław Trocki
				Grupa: A
Prowadzący: bryg. mgr inż. Wojciech Zegar	Data wykonania: 16.02.2002r.	Data złożenia: 02.03.2002r.	Ocena:

Cel ćwiczenia:

Celem ćwiczenia jest wyznaczenie wydatku rzeczywistego Q_rz oraz wydatku teoretycznego Q_t na kryzie korzystając z tabeli pomiarowej uzyskanych wyników, a następnie porównanie tych dwóch wielkości określających współczynnik wydatku kryzy α.

Schemat stanowiska pomiarowego:

Stanowisko pomiarowe składa się z pomiarowej rury poziomej, pionowej rury z kryzą. Przepływ powietrza jest wymuszony wentylatorem odśrodkowym, napędzanym silnikiem elektrycznym. Regulację wydatku uzyskuje się poprzez zmianę położenia regulatora wydatku.

Ciśnienie dynamiczne jest mierzone rurką Prandtla, która jest przesuwana w płaszczyźnie prostopadłej do kierunku przepływu. Do kontroli ustawienia rurki pomiarowej względem ścianki rury służy odpowiednia podziałka. Mikromanometr jest połączony różnicowo z rurką Prandtla. Ciśnienie różnicowe na kryzie jest wskazywane przez drugi mikromanometr.

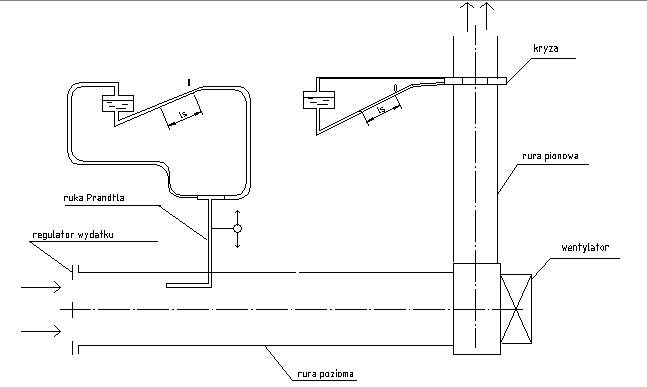
Tabela pomiarów:

Lp.	Położenie rurki Prandtla R [mm]	Wychylenie się cieczy w manometrze Lp [mm]	Wychylenie się cieczy na kryzie Lk [mm]
1	48	144	85
2	45	144	85
3	40	145	84
4	35	147	86
5	30	145	84
6	25	145	84
7	20	142	85
8	15	132	84
9	12	122	85
10	10	130	85
11	8	112	85
12	6	105	85
13	4	100	85
14	2	80	85

Tabela wyników:

Lp.	Obliczone ciśnienie dynamiczne Pd [Pa]	Obliczona prędkość powietrza Vpow(R) [m/s]	Obliczony iloczyn R·Vpow(R) [m^2/s]
1	22,03	5,82	0,279
2	22,03	5,82	0,262
3	22,19	5,84	0,234
4	22,49	5,88	0,206
5	22,19	5,84	0,175
6	22,19	5,84	0,146
7	21,73	5,78	0,116
8	20,20	5,57	0,083
9	18,67	5,35	0,064
10	19,89	5,33	0,055
11	18,36	5,31	0,042
12	16,06	4,97	0,030
13	15,30	4,85	0,019
14	12,24	4,33	0,009

Przykładowe obliczenia:

1. Obliczanie ciśnienia dynamicznego:

Dane: Obliczenia:

L_p = 0,142 [m] p_d =L_p · n_p · ρ_cm · g

n_p. = 1/50 = 0,02 p_d = 0,142 · 0,02 · 780 · 9,81

ρ_cm = 780 [kg/m³] p_d = 21,73[Pa]

g = 9,81 [m/s²]

Dane: Obliczenia:

L_p = 0,105 [m] p_d =L_p · n_p · ρ_cm · g

n_p. = 1/50 = 0,02 p_d = 0,105 · 0,02 · 780 · 9,81

ρ_cm = 780 [kg/m³ ] p_d = 16,06 [Pa]

g = 9,81 [m/s²]

2. Obliczanie prędkości powietrza:

Dane: Obliczenia:

p_d = 22,49 [Pa] V_pow(R) = √(2pd/ ρ_pow)

ρ_pow = 1,3 [kg/m³] V_pow(R) = 5,88 [m/s]

Dane: Obliczenia:

p_d = 16,06 [Pa] V_pow(R) = √(2p_d/ ρ_pow)

ρ_pow = 1,3 [kg/m³] V_pow(R) = 4,97 [m/s]

3. Obliczanie iloczynu:

Dane: Obliczenia:

R = 0,035 [m] R·V_pow(R) = 0,206 [m²/s]

V_pow(R) = 5,88 [m/s]

Dane: Obliczenia:

R = 0,006 [m] R·V_pow(R) = 0,030 [m²/s]

V_pow(R) = 4,97 [m/s]

4. Obliczenie pola trójkąta z wykresu:

Dane: Obliczenia:

d = 24 [cm] F = 1/2 · d · h

h = 14,5 [cm] F = 174 [cm²]

5. Obliczanie wydatku rzeczywistego:

Obliczenie κ z wykresu:

x → 1 cm = 0,002 [m] κ = x · y = 0,00004 [m³/s/cm²]

y → 1 cm = 0,02 [m²/s]

Dane: Obliczenie:

Π = 3,14 Q_rz = 2 · Π · F · κ

F = 174 [cm²] Q_rz = 0,0437 [m³/s]

κ = 0,00004 [m³/s/cm²]

6. Obliczenia dla kryzy:

► obliczenie średniego wychylenia na kryzie:

L_śr = 85 [mm]

► obliczenie ciśnienia różnicowego na kryzie:

Dane: Obliczenia:

L_kśr = 0,085 [m] p = L_kśr · n_k · ρ_cm · g

n_k = 1/10 = 0,1 p = 65,0 [Pa]

ρ_cm = 780 [kg/m³]

g = 9,81 [m/s²]

► obliczenie modułu kryzy:

Dane: Obliczenie:

d_k = 0,0756 [m] m = ( d_k/d_r)²

d_r = 0,096 [m] m = 0,62

6. Obliczanie wydatku teoretycznego:

Dane: Obliczenie:

m = 0,62 Q_t = [1/√(1-m²)]·[(Πd_k²)/4]·[√(2p/ ρ_pow)]

Π = 3,14 Q_t = 0,057 [m³/s]

d_k = 0,0756 [m]

p = 65,0 [Pa]

ρ_pow 1,3 [kg/m³]

7. Obliczenie współczynnika wydatku kryzy:

Dane: Obliczenie:

Q_rz = 0,0437 [m³/s] α = Q_rz/Q_t

Q_t = 0,057 [m³/s] α = 0,76

Wnioski:

Obliczony wydatek rzeczywisty Q_rz = 0,0437w porównaniu z wydatkiem teoretycznym Q_t = 0,057 jest mniejszy. Różnica między dwoma wydatkami (rzeczywistym a teoretycznym) spowodowana jest:

---