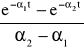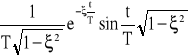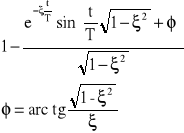Jeśli charakterystykę skokową
![]()
a wiec funkcję podstawową czasową, uważać za funkcję podstawową czyli oryginał, a następnie poszukiwać funkcji przekształconej czyli odwzorowania w dziedzinie częstotliwości, to można w tym celu posłużyć się przekształceniem Laplac'e wykorzystującym operator zespolony.
![]()
gdzie: ![]()
- część rzeczywista liczby zespolonej S,
![]()
- pulsacja ![]()
,
s - operator zespolony.
Za pomocą całki Laplac'e
![]()
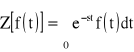
Charakterystyka skokowa jest odwzorowana w dziedzinie częstotliwości w taki sposób, że transformata wielkości wyjściowej xwyjścia(s) jest równa iloczynowi transmitancji operatorowej F(s) i transformaty wielkości wejściowej xwejściowe(t). W przypadku charakterystyki skokowej f(t) wielkość wejściowa xwejściowe(t) jest funkcją skokową xwejściowego o amplitudzie „1”. Zatem transformata Laplac'e skoku jednostkowego wynosi:
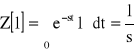
Przekształcenie Laplace'a przyporządkowuje funkcji f(t) zmiennej rzeczywistej t funkcję F(s) zmiennej zespolonej s według wzoru zwanego całką Laplace'a
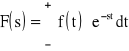
Funkcja f(t) nazywa się oryginałem, a odpowiadającą jej funkcja F(s) - transformatą.
W automatyce używane jest tzw. Jednostronne przekształcenie Laplac'e, w którym transformata związana jest z oryginałem zależnością
![]()
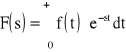
Stosując jednostronne przekształcenie Laplace'a zakłada się, że dla t < 0 jest f(t)≡0. Przyporządkowanie oryginałowi f(t) transformaty F(s) zgodnie z wzorem ( ) przyjęto zapisywanie za pomocą symbolu α.
![]()
czyli
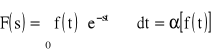
Nie wszystkie funkcje zmiennej rzeczywistej mają swoje transformaty. Aby można było wyznaczyć transformatę funkcji f(t) muszą być spełnione warunki:
f(t) ma pochodną
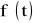
w każdym przedziale skończonym,istnieje zbiór liczb rzeczywistych c, dla których całka
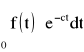
jest absolutnie zbieżna.
Jeżeli transformata funkcji f(t) jest określona tylko dla pewnego zbioru wartości zmiennych zespolonych „s”, przyjmuje się umownie, że istnieje ona i jest taka sama również dla pozostałych wartości zmiennej zespolonej.
Przekształcenie Laplace'a można traktować jako prawo odpowiedzialności między dwoma zbiorami funkcji
![]()
oryginał transformata
Idea metody operatorowej stosowanej w automatyce pozwala znacznie upuścić tok obliczeń. Polega na znalezieniu przekształcenia pozwalającego zastąpić równanie różniczkowo - całkowe zwykłymi równaniami algebraicznymi. Oryginały i odpowiadające im transformaty przedstawia tabela nr.1. Rozwiązując różniczkowe równania liniowe o stałych współczynnikach, opisujące dynamikę układu za pomocą transformacji Laplace'a, uzyskuje się nowe funkcje zmiennej zespolonej. Obie strony równania poddajemy przekształceniu Laplace'a, otrzymujemy równania algebraiczne, które według tabeli zależności odwrotnych przekształcając transformatę na oryginał czyli na funkcję czasu. Należy powiedzieć, że istnieje odwrotne przekształcenie Laplace'a α-1 które przyporządkuje funkcji F(s) zmiennej zespolonej „s” funkcję f(t) zmiennej rzeczywistej „t” według wzoru zwanego całką Riemanna - Mellina.
![]()
Do wyznaczenia oryginału danej funkcji zmiennej zespolonej wykorzystuje się własności przekształcenia Laplace'a oraz tablicę transformat. W celu znalezienia oryginału rodzaju transformaty należy ją włożyć na sumę ułamków prostych a oryginały poszczególnych ułamków wyznaczyć za pomocą tablic.
W sposób równoważny jak równanie różniczkowe układ automatyki opisuje wielkość zwaną transmisją lub transmitancją operatorową. Transmitancję operatorową elementu, układu, członu lub obiektu nazywamy stosunek transformaty wielkości wyjściowej Y(s) do transformaty wielkości wejściowej X(s) tego elementu, układu lub obiektu przy zerowych warunkach początkowych
![]()
Przyjęto wpisywać transmitancję operatorową wewnątrz prostokątów przedstawiających poszczególne elementy na schematach blokowych układów automatyki.
gdzie: X(s) - wielkość wejściowa (sygnał wejściowy),
Y(s) - wielkość wyjściowa (sygnał wyjściowy),
G(s) - transmitancja operatorowa członu.
Strzałki oznaczją kierunek przekazywania sygnału oraz wskazują, że nie ma oddziaływania sygnału wyjściowego na wejściowy czyli jednokierunkowość członu.
Z transmitancji operatorowej można wyznaczyć charakterystykę ststyczną i dynamiczną elementu, układu, obiektu i odwrotnie z charakterystyki dynamicznej można wyznaczyć transmitancję operatorową.
Rozwiązywanie liniowych równaań różniaczkowych zwyczajnych za pomocą przekształcenia Laplace'a polega na ich algebraizacji. Zwyczjane równanie różniczkowe ze stałymi współczynnikami w których f(t) jest zwaną funkcją zmiennej rzeczywistej oraz zwane są warunki początkowe i aby rozwiązać należy:
podać je przekształceniu Laplace'a z uwzględnieniem waruknów początkowych,
wyznaczyć transformatę G(s) szukanej funkcji,
doprowadzić tę transfotmatę do postaci:
![]()
wyznaczyć szukaną funkcję zmiennej rzeczywistej
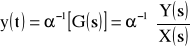
.
Działając według przedstawionych reguł można wyznaczyć transformatę funkcji jednostkowej f(t)=1(t) czyli skoku jednostkowego przyjmując, że:
1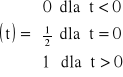
TABLICA 1
Transformaty Laplace'a najczęściej spotykanych funkcji
Lp. |
Oryginał f(t) |
Transformata F(s) |
1. |
|
1 |
2. |
1(t) skok jednostkowy (funkcja Heviside'a) |
|
3. |
t |
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
|
11. |
|
|
12. |
|
|
13. |
|
|
14. |
|
|
15. |
|
|
16. |
|
|
17. |
|
|
18. |
|
|
cd. tablicy 1.
19. |
|
|
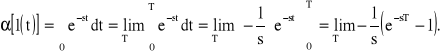
Granica jest określona dla takich s, których część rzeczywista jest większa od zera a więc, jeśli
![]()
,
to
![]()
,
stąd
![]()
.
WYKŁAD 6
Liniowe człony dynamiczne
Operatory liniowe (opisane równaniami różniczkowymi liniowymi) spełniają spełniają dwa warunki:
![]()
dla wszystkich wielkości x i y należących do określonego zbioru oraz stałej liczby C.
Warunek:
![]()
oznacza, że dokonanie transformacji T na wielkości ![]()
(gdzie c jest liczbą stałą) jest równoznaczne dokonaniu transformacji T na wielkości x i pomnożeniu otrzymanego wyniku przez „c”. Innymi słowy: wielkość stałą c można wyciągnąć przed znak operatora.
Warunek:
![]()
oznacza, że operatory liniowe mają własność addytywności, to jest możliwości dokonania transformacji na sumie wielkości x i r co jest równoznaczne zsumowaniu transformacji dokonanej na „x” i transformacji dokonanej na „r”.
Dotychczasowe rozważania pokazały, że człon dynamiczny można opisać za pomocą równania różniczkowego. Równanie różniczkowe wyrażające zależności pomiędzy sygnałem wejściowym i wyjściowym nazywa się równaniem dynamiki (równaniem ruchu). Postać równania dynamiki lub transmitancja określona z tego równania stanowi kryterium, według którego klasyfikuje się człony automatyki. Jeśli na przykład jest rozważane równanie różniczkowe drugiego rzędu, to opisywany przez nie człon dynamiczny jest nazywany członem rzędu drugiego np. członem inercyjnym rzędu drugiego. W ogólności układ może być dowolnego rzędu. W równaniu różniczkowym opisującym człon dynamiczny n - tego rzędu wielkość wyjściowa Xwyjściowe(t) występuje wraz z pochodnymi do n - tego rzędu włącznie. Wielkość wejściowa Xwejściowa(t) występuje również nie tylko w postaci pierwotnej, ale i wraz z pochodnymi - czyli w członie dynamicznym występują zjawiska nie tylko typu inercji (bezwładności, o późnienia), ale także wyprzedzania.
Zatem równanie różniczkowe członu dynamicznego ma postać ogólną:
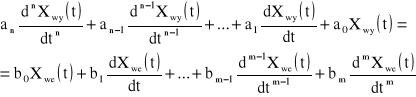
![]()
czyli
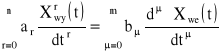
.
Dla uproszczenia zapisu w równaniu powyższym upuszczono składnik stałej, wskazujący, na jakim poziomie przebiega proces czyli a0=1. Składnik stały można pominąć gdy obliczenia są prowadzone na względnym poziomie zerowym lub gdy wielkości Xwe oraz Xwy są wielkościami względnymi bezwymiarowymi.
Współczynnikami ar o indeksach r = 0,1,2 do n oraz bμ o indeksach μ = 0,1,2 są liczbami rzeczywistymi stałymi.
Przyrównując do zera lewą stroną równania różniczkowego ( ) do zera
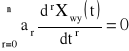
otrzymuje się równanie różniczkowe jednorodne, opisujące przebieg przejściowy.
Jeżeli którakolwiek z pochodnych rzędu
![]()
występuje ze współczynnikiem ujemnego, to człon dynamiczny będzie wykazywał przebiegi narastające w czasie.
Z równania różniczkowego po podstawieniu sygnału wyjściowego
![]()
o stałej amplitudzie ![]()
i zmiennej pulsacji ω, możemy wyznaczyć przebieg sygnału wyjściowego w zależności od częstotliwości, tzn. transmitancję widmową
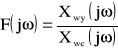
.
Poszukiwanie rozwiązania drogą klasyczną ma sens tylko dla równań różniczkowych niskiego rzędu. Po rozkładzie transmitancji widmowej moduł i fazę
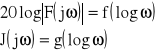
można otrzymać charakterystyki częstotliwościowe członu dynamicznego.
Jeśli sygnał Xwejściowy Xwe(t) członu dynamicznego jest funkcją skokową Xwe o amplitudzie jednostkowej „1” i jeśli wszystkie warunki początkowe w chwili skoku są zerowe, czyli
![]()
to jako rozwiązanie równania różniczkowego otrzymuje się charakterystykę skokową
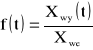
która przedstawia przebieg przejściowy zależy od czasu. Charakterystykę skokową wyznacza się z równania różniczkowego tylko w przypadku członów niskich rzędów nakład obliczeń jest zbyt duży. Mając daną charakterystykę skokową, to za pomocą przekształcenia Laplace'a można wyznaczyć transmitancję operatorowe. Transmitancję operatorową z równania różniczkowego dynamiki członów podstawowych przy zerowych warunkach początkowych wyznaczamy. a0 = Różniczkowanie
![]()
zastępujemy operatorem „s”
Dla równania otrzymuje się:
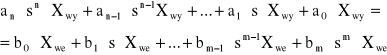
czyli
![]()
.
Przy tych warunkach transmitancja operatorowa ma postać:
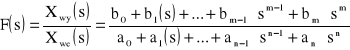
.
Postać algebraiczna jest znacznie dogodniejsza do obliczeń niż postać równania różniczkowego. Po przez odwrotne przekształcenie transformaty Laplace'a do funkcji czasowej można wyznaczyć charakterystyki skokowe dla członów dynamicznych. Wtedy w dalszych rozważaniach posługiwać się będziemy transmitancją operatorową, oraz charakterystyką skokową członu automatyki.
Przystępując do układania schematu strukturalnego określonego układu regulacji, powinniśmy wyodrębnić jego typowe człony aby wykorzystać znajomość właściwości dynamicznych tych członów.
Człon bezinercyjny (proporcjonalny)
Operator transformacji proporcjonalnej, który przekształca stan wejścia „x” na stan wyjścia „y” przez pomnożenie stanu wejścia przez pewną liczbę rzeczywistą, a więc w ten sposób, że
![]()
gdzie: k - stała rzeczywista nosi nazwę przepustowości transformacji.
Należy podkreślić, że operator transformacji i proporcjonalnej nie jest identyczny ze stałą k. Operator w danym przypadku to reguła postępowania i pomnóż „x” przez „k”.
Między wielkością wejściową a wyjściową członu bezinercyjnego nie ma żadnej inercji ani zależności czasowej. Jedynie amplituda wielkości wyjściowej może być większa, mniejsza lub równa amplitudzie na wejściu.
Stosunek wielkości wyjściowej ![]()
do wielkości wejściowej ![]()
określa działanie członu w dziedzinie czasowej
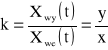
przy czym k oznaczono wzmocnienie. Charakterystyka skokowa ma postać:
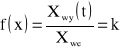
lub

gdy
![]()
przy czym Xwy jest skokową zmianą wielkości wejściowej Xwe. Transmitancję operatorową można napisać:
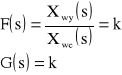
lub
![]()
![]()
a odpowiedź skokowa
![]()
Element bezinercyjny - proporcjonalny opisany więc jest równaniem:
![]()
a transmitancja elementu ma postać:
![]()
.
Element można uznać za bezinercyjny, gdy jego stała czasowa w porównaniu ze stałymi czasowymi połączonych z nim elementów jest bardzo mała. Wielkością charakteryzującą element bezinercyjny jest wzmocnienie statyczne „k”. Można przyjąć, że elementy pomiarowe, czujniki i przetworniki są elementami bezinercyjnymi o wzmocnieniu „k”. W elementach o takiej dynamice, po podaniu na wejście sygnału określonego funkcją skokową, na wejściu otrzymamy sygnał skokowy, a o innej wysokości skoku. Przykładem elementu bezinercyjnego - członu proporcjonalnego może być dzielnik napięcia.
Wielkością wejściową jest napięcie U1, a wielkością wyjściową napięcie U2. Ze zmianą napięcia U1 zamienia się napięcie U2 bezinercyjne, czyli bez przesunięcia czasowego. Stosunek amplitud jest równy:
![]()
a współczynnik proporcjonalności “k” mniejszy od jedności.
Transmitancję operatorową dzielnika napięcia w którym wielkością wejściową jest napięcie U1, a wielkością wyjściową napięcie U2 na postawie prawa Ohma możemy napisać:
![]()
czyli
![]()
stąd
![]()
Po transformacji Laplace'a otrzymamy:
![]()
stąd transmitancja:
![]()
.
Wielkością wejściową jest tu prędkość obrotowa n mierzona w obrotach na minutę ![]()
, wielkością wyjściową jest napięcie UT[V].
Wzmocnienie k określa się wzorem:
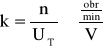
gdzie: k - wzmocnienie,
n - obroty tachoprądniczki, ![]()
,
U - napięcie wyjściowe [V].
Wprowadzając wielkości bezwymiarowe stosowane w automatyce otrzymujemy:
![]()
i w ten sposób stosunek wielkości wyjściowej do wejściowej jest bezwymiarowy i niezależny od czasu.
Człon inercyjny rzędu pierwszego
Inercja jest określana jako bezwładność i jest ona naturalną własnością obiektu regulacji powodującą opóźnienie w czasie wielkości wyjściowej w stosunku do wielkości wejściowej. W członie dynamicznym inercyjnym rzędu pierwszego wielkość wyjściowa nie zmienia się w tej samej chwili po zamianie wielkości wejściowej. Charakterystykę skokową członu inercyjnego otrzymujemy rejestrując przebieg sygnału na wejściu członu po wprowadzeniu skokowej zamiany sygnału wejściowego.
Postać ogólna funkcji czasowej członu inercyjnego rzędu pierwszego jest określana przez równanie:
![]()
lub
![]()
gdzie: T - stała czasowa członu,
k - współczynnik wzmocnienia lub proporcjonalności.
Symbol T oznacza własność elementu dynamicznego, która przy zależnościach obowiązujących w tym członie jest wielkością stałą i nazywa się stałą czasową.
Jeśli zmiana sygnału wejściowego jest skokowa, to zmiana wielkości wyjściowej stanowi charakterystykę skokową typu:
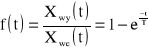
Przekształcenie Laplace'a prowadzi do transmitancji operatorowej
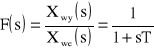
lub
![]()
ponieważ człon inercyjny może być rozpatrywany jako połączenie szeregowe członu bezinercyjnego i członu inercyjnego o współczynnikach wzmocnienia „k”.
Sposób wyznaczenia stałej czasowej T z wykresu odpowiedzi skokowej pokazano na rys.4. Stała czasowa jest to czas określony rzutem odcinka stycznej OA na asymptotę wyznaczającą wartość ustaloną wielkości wyjściowej.
Po czasie T od zaistnienia wymuszenia na wejściu członu wielkość wyjściowa ulega zmianie o ok. 0,64 wartości ustalonej na wyjściu członu.
Przykładem takiego członu może być kondensator „C” ładowany przez rezystor „R”.
Po przyłożeniu na wejście obwodu napięcia w układzie płynie prąd „I” i na okładkach kondensatora gromadzi się ładunek elektryczny, wzrasta napięcie UC, aż ustali się na poziomie napięcia wejściowego.
Niech sygnał wejściowy u(t)=U0⋅1(t), a sygnał wyjściowy uc to wzmocnienie statyczne
![]()
a stała czasowa
![]()
gdzie: C - pojemność kondensatora [F],
R - rezystancja [Ω]
T - stała czasowa [s].
Człon inercyjny rzędu drugiego może być uzyskany przez połączenie dwóch elementów inercyjnych rzędu pierwszego o stałych czasowych T1 i T2. W ten sam sposób, przez szeregowe połączenie n elementów inercyjnych można otrzymać element rzędu n- tego. W obiektach automatycznej regulacji zwykle rozdziela się inercyjności występujące w obiekcie tak aby móc je rozpatrywać jako człony pierwszego rzędu. Symbol blokowy dynamicznego drugiego rzędu odzwierciedla postać przebiegu przejściowego.
W zależności od charakteru pierwiastków mianownika funkcji transformacji, odpowiedzi obiektów inercyjnych drugiego rzędu mogą być aperiodyczne - przy rzeczywistych pierwiastkach transmitancji lub oscylacyjnie przy pierwiastkach zespolonych.
Działanie członu całkującego polega na tym, że zmiana sygnału wyjściowego Xwy jest proporcjonalna do wielkości wejściowej Xwe. Jeśli wielkość wejściowa jest równa zeru, to wielkość wyjściowa nie ulega zmianie, może jednak przyjmować dowolną wartość z dopuszczalnego przedziału. Gdy wielkość wejściowa jest mała, to zmiana wielkości wyjściowej następuje powoli - jeśli jest duża, to zmiana wielkości wyjściowej jest możliwa tylko do chwili osiągnięcia pewnej wartości granicznej, zwanej również poziomem nasycenia. W zakresie sterowania słuszne jest w dziedzinie czasowej równanie
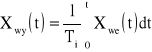
Działanie członu całkującego przedstawia stała czasowa Ti, inaczej czas całkowania. Czas całkowania można wyznaczyć wtedy gdy wielkość wejściowa Xwe i wyjściowa Xwy są jednakowymi wielkościami fizycznymi. Jeśli w chwili t=0 wielkość wejściowa zmienia się skokowo od wartości zerowej do wartości skończonej Xwe to wielkość wyjściowa rośnie liniowo z biegiem czasu w taki sposób, że przyrost wielkości wyjściowej Xwy po czasie Ti staje się równy wielkości wejściowej Xwe.
W ten sposób również określana charakterystyczna skokowa
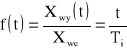
lub opisane równaniem różniczkowym
![]()
gdzie: Ti - stała czasowa całkowania,
k - prędkościowy współczynnik wzmocnienia członu.
Nazwa „człon całkujący” określa funkcję członu, często używana jest nazwa „człon astatyczny” pochodzi stąd, że człon ten nie ma charakterystyki statycznej, a stan ustalony istnieje tylko przy zerowej wartości sygnału wejściowego. Idealnym modelem członu całkującego jest zbiornik cylindryczny w którym zarówno dopływ jak i odpływ są wymuszane i niezależne od poziomu cieczy.
Jeżeli jako wielkość wyjściową przyjmujemy poziom cieczy w zbiornikach „h”, a jako wielkość wejściową - otwarcie zaworu doprowadzającego ciecz do zbiornika lub złączenie pompy odprowadzającej ciecz ze zbiornika. Przedstawiony przykład członu całkującego pokazuje, że człon taki mógłby być nazwany „nadgromadzającym” albo „akumulującym”.
Porównajmy odpowiedzi skokowe członu całkującego i inercyjnego. Odpowiedź skokowa członu inercyjnego może być zastępowana z pewnym przybliżeniem linią prostą. Nasuwa się wniosek, że człon inercyjny rzędu pierwszego może przez pewien czas od wprowadzenia na jego wejście wymuszenia skokowego stanowić przybliżenie członu całkującego. Przy bardzo dużych stałych czasowych człon inercyjny rzędu pierwszego traktować jako człon całkujący.
Człon różniczkujący
W rzeczywistości nie ma elementu którego sygnał wyjściowy byłby pochodną sygnału wejściowego. Budując układy strukturalne w automatyce wydziela się człony dla których model członu różniczkującego idealnego jest w pełni uzasadniony.
Wielkość wyjściowa członu dynamicznego reaguje wartością różną od zera tylko wtedy, gdy wielkość wejściowa ulega zmianie, zachodzi różniczkowanie wielkości wejściowej. Działanie opisane jest równaniem:
![]()
Stała czasowa TD nazywa się czasem różniczkowania i określa skuteczność oddziaływania wielkości wejściowej na wielkość wyjściową.
Członem różniczkującym idealnym nazywamy układ opisany równaniem różniczkowym
![]()
Transmitancja operatorowa wynosi
![]()
gdzie: k - współczynnik wzmocnienia członu.
Rzeczywistym członem różniczkującym nazywamy człon opisany równaniem:
![]()
Transmitancja operatorowa wynosi:
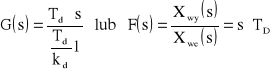
gdzie: kd - dynamiczny współczynnik wzmocnienia członu,
Td - stała czasowa różniczkowania.
Przy założeniu, że wielkość wejściowa Xwe i wielkość wyjściowa Xwy są jednakowymi wielkościami fizycznymi t0 czas różniczkowania można wyznaczyć przy liniowej względem czasu zmianie wielkości wejściowej.
Gdy wielkość wejściowa Xwe zmienia się - począwszy od t=0 zgodnie z funkcją
![]()
to zgodnie z zależnością opisującą działanie członu różniczkującego ( ) oznacza to, że po upływie czasu TD zmiana wielkości wejściowej musi odpowiadać dokładnie wielkości wyjściowej
![]()
.
Z porównania wykresów członów całkującego i różniczkującego wynika, że działanie członu różniczkującego jest dokładnym przeciwstawieństwem działania członu całkującego. Wprowadzamy do członu różniczkującego skokową zmianę wielkości wejściowej Xwe w chwili t=0, powinno się otrzymać w tejże chwili wielkość wyjściową teoretycznie nieskończenie wielką. Mówi się o funkcji szpilkowej lub impulsie Diraca. Iloczyn amplitudy wielkości wyjściowej i czasu jej trwania ts≈0 jest równa iloczynowi amplitudy wielkości wejściowej i czasu różniczkowania
![]()
.
W praktyce nie są możliwe nieskończone amplitudy. Transmisja operatorowa ma postać:
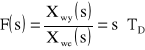
.
Członem różniczkującym nazwano układ, którego wartość sygnału wejściowego jest proporcjonalna do szybkości zmian sygnału wejściowego, natomiast nie zależy od wartości tego sygnału. Ze względu na funkcję człon różniczkujący nazywany jest członem „forsującym”. Rzeczywiste człony różniczkujące realizują operację różniczkowania w przybliżeniu. Wielkością wejściową przesunięcia tłoka „x”, a zbiornika z gazem. Przesunięcie tłoka powoduje sprężanie lub rozprężanie (zależnie od kierunku ruchu tłoka) gazu w zbiorniku.
Rozpoczyna się wyrównywanie ciśnień przez zawór przelotowy po obu stronach tłoka. Po pewnym czasie, zależnym od pojemności zbiornika i drożności zaworu przelotowego, ciśnienia w zbiorniku wyrównuje się z ciśnieniem panującym po drugiej stronie tłoka czyli powraca do wartości, jaką miało ciśnienie przed przestawieniem tłoka.
Przykładem członu różniczkującego jest również kondensator przewodzący prąd przy zmiennym napięciu.
Pojemność kondensatora wyraża wzór:
|
(a) |
|
(b) |
Po podstawieniu zależności (b) do (a) otrzymujemy:
![]()
Oznaczając:
![]()
otrzymamy:
|
(c) |
Transformata wielkości wyjściowej określona z równania (c) jest następująca:
![]()
stąd transmitancja
![]()
W układach regulacji automatycznej spotyka się często z koniecznością uwzględnienia czasu transportu materiału, dostawy paliwa oraz czasu przepływu sygnału sterującego np. jeśli zawór dopływu gazu do pieca został umieszczony daleko od pieca. Wówczas przy analizie pracy całego układu automatyki należy uwzględnić opóźnienie między wytworzeniem sygnału sterującego w regulatorze a otrzymaniem tego sygnału przez siłownik.
WYKŁAD 7
Stabilność liniowych układów regulacji automatycznej
W celu uzyskania dynamicznej interpretacji podstawowego wzoru regulacji
![]()
nasuwa się przez analogię możliwość, że operator sprzężenia zwrotnego
![]()
wyrażający działanie regulatora można uważać za sumę nieskończonego szeregu geometrycznego:
![]()
przy czym wzór ten ma sens (czyli jest zbieżny), gdy wartość bezwzględna SR jest mniejsza od 1, czyli
![]()
.
Podstawowy wzór regulacji przyjmuje wówczas postać:
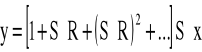
lub
![]()
Dla analizy procesu regulacji trzeba uwzględnić, że odbywające się w układzie regulacji procesy są funkcją czasu. Załóżmy, że ma regulator w danym czasie t oddziaływuje wielkość
![]()
czyli wartość zmiennej y z powszedniego okresu. Wówczas podstawowy wzór regulacji przyjmuje postać:
|
(x) |
Innymi słowami przyjmujemy, że istnieje pewne opóźnienie działania regulatora w czasie, przy czym to opóźnienie możemy przyjąć za jednostkę mierzenia czasu. Podstawowy wzór regulacji możemy przekształcić
![]()
wprowadzając do wzoru operator E-1 i wyznaczając yt otrzymujemy wzór:
![]()
,
który jest analogiczny do podstawowego wzoru regulacji w przypadku działania natychmiastowego (bez opóźnień).
W równaniu różniczkowym (x) można dokonać redukcji sprężenia zwrotnego ![]()
, będący odchyleniu zmiennej yt od stanu równowagi układu określanego wzorem
![]()
.
Otrzymujemy wówczas:
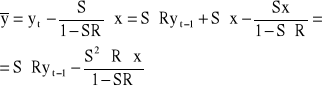
czyli
![]()
.
W rezultacie mamy zredukowane równanie różniczkowe:
|
(y) |
gdyż
![]()
Rozwiązywanie zredukowanego równania (y) jest wyrażone
|
(z) |
Rozwiązywanie pozwala zbadać przebieg procesu regulacji w czasie.
Warunkiem stabilności układu regulacji jest, aby bezwzględna wartość operatora SR była mniejsza od 1
czyli
![]()
Warunek ![]()
można zapisać w postaci
![]()
gdzie: ![]()
- moc regulatora,
![]()
- moc układu regulowanego.
Warunkiem stabilności układu regulacji jest aby moc regulatora była mniejsza od odwrotności mocy układu regulowanego. W takim przypadku mówimy, że sprężenie zwrotne kompensuje działanie układu, czyli skutecznie zmniejsza zakłócenie powstałe w układzie. Gdy:
![]()
,
działanie regulatora jest zbyt silne i proces zachodzący w danym układzie oddala się od stanu równowagi. Mówimy wówczas, że zachodzi kumulacyjne sprzężenie zwrotne i moc regulatora jest większa od mocy układu regulowanego.
W przypadku gdy:
![]()
wtedy moc regulatora jest równa mocy układu regulowanego a układ pracuje na granicy stabilności, likwiduje powstałe zakłócenia a, każdy stan jest stanem równowagi.
Operatorom regulatora i układu regulowanego można nadać znak plus lub minus. W przypadku, gdy transformacja polega na pomnożeniu przez liczbę rzeczywistą (transformacja proporcjonalna), przypisywania operatorom określonego znaku nie powoduje żadnych trudności. Gdy jako znak operatora przyjmujemy znak wymienionej liczby rzeczywistej to w przypadku operatorów innych transformacji za opatrzenie operatora w znak oznacza pomnożenie jego przez jednostkowy operator proporcjonalności +1, lub -1. Znak operatorów wybieramy tak, że operatorom R i S nadajemy ten sam znak, kiedy zmiana stanu wyjścia regulatora ma ten sam znak, co zmiana stanu wyjścia układu regulowanego; znak różny nadajemy w porządku odwrotnym. Zakładając, że operatorowi został przyporządkowany określony znak, łatwo zauważyć na podstawie wzoru (z), że jeśli znak operatora S jest taki sam jak operatora R czyli:
![]()
to przebieg zaburzenia danym układzie jest jednostronny (monotoniczny), czyli w kolejnych następujących po sobie okresach układ jest stale powyżej lub poniżej poziomu równowagi.
W przypadku gdy r i S mają taki sam znak w układzie zachodzi dodatnie sprężenie zwrotne. Jeśli operatory S i R mają znaki różne w układzie regulacji zachodzi sprężenie zwrotne ujemne. Wówczas zaburzenie przebiega w sposób oscylacyjny. Z wzoru (z) wynika, że odchylenie ![]()
od stanu równowagi w kolejnych okresach zmienia znak, ponieważ wykładnik t jest na przemian nieparzysty i parzysty. Oscylacyjnie są rosnące lub gasnące lub stałe w zależności od tego, czy
![]()
.
Wyniki zostały ujęte w tabeli, która podaje obszary odpowiadające różnym wartością iloczynu ![]()
Obszar oscylacji |
Obszar monotoniczności |
|||||
SR |
||||||
Obszar niestabilności układu |
Obszar stabilności układu |
Obszar niestabilności układu |
||||
|
Lewa granica Obszaru stabilności |
Praw granica obszaru stabilności |
|
|||
Zapewnienie stabilności w pracy układu regulacji automatycznej jednym z podstawowych wymagań przy jego projektowaniu. Pojęcie stabilności jest intuicyjne i oznacza, że układ po wyprowadzeniu do ze stanu równowagi sam powraca do tego stanu. Istnieje wiele definicji stabilności o różnej interpretacji pojęcia „stan równowagi”. Dla przykładu drgania nierosnące są niekiedy jako stan równowagi układu i sąd dwupołożeniowa regulacji automatyczna temperatury traktowana jest jako praca stabilna.
Wywód przeprowadzony w pierwszej części wykładu dotyczy „podstawowego układu automatyki” można powiedzieć układu odniesienia, ale projektując układy automatycznej regulacji trzeba rozpatrywać człony rzeczywiste i układy zbudowane z członów w różnej konfiguracji.
Przyjmując definicję stabilności wg. Laplace'a która mówi, że układ liniowy jest stabilny jeżeli jego odpowiedź na wymuszenie (zakłócenie) o ograniczonej wartości jest ograniczona. Naturalną drogą przekonania się czy dany układ jest stabilny jest rozwiązanie równania ruchu opisującego dany układ.
Układy automatyki opisywane są za pomocą równań różniczkowych (pełnych) niejednorodnych.
Rozwiązanie równania różniczkowego niejednorodnego y(t) jest sumą rozwiązań
![]()
,
gdzie: y0(t) - jest rozwiązaniem ogólnym równania jednorodnego,
ys(t) - jest rozwiązaniem szczególnym równania niejednorodnego.
Rozwiązanie ogólne równania jednorodnego y0(t) reprezentuje ruch swobodny układ, natomiast rozwiązanie szczególne ys(t) równania niejednorodnego reprezentuje ruch wymuszony układu. Rozwiązanie ogólne równania niejednorodnego będące sumą rozwiązań y0(t) i ys(t) mówią o zachowaniu się układu pod wpływem zakłóceń.
Warunkiem stabilności układu jest tłumienie ruchu swobodnego. A więc dla stwierdzenia stabilności układu należy badać rozwiązanie ogólne równania jednorodnego y0(t).
![]()
gdzie: s1,s2,...,sn - pierwiastki równania charakterystycznego.
Aby po upływie dostatecznie długiego czasu wielkość y0(t) była równa zeru, pierwiastki s1,s2,...,sn muszą być rzeczywiste ujemne, bądź zespolone z częścią rzeczywistą ujemną. Wynika z tego, że kryterium stabilności można sformułować następująco:
„Układ automatyki jest stabilny, jeżeli wszystkie pierwiastki równania charakterystycznego układu leżą w lewej półpłaszczyźnie płaszczyzny pierwiastków”.
Układ liniowy, którego równanie charakterystyczne posiada jeden pierwiastek zerowy jest układem stabilnym nieasymptotycznie. W przypadku pierwiastków zerowych wielokrotnych układ jest niestabilny. Badanie stabilności liniowych układów automatyki sprowadza się do badania położenia pierwiastków równania charakterystycznego układu w płaszczyźnie zmiennej zespolonej „s”.
W przypadku, gdy znane są pierwiastki równania charakterystycznego, zagadnienie stabilności układu jest rozstrzygnięte.
Obliczenie pierwiastków równania charakterystycznego nie zawsze jest łatwe, dlatego też poszukiwano metod umożliwiających stwierdzenie czy pierwiastki znajdują się w lewej płaszczyźnie pierwiastków (Gaussa).
Trudności w obliczaniu pierwiastków równania charakterystycznego skłoniły do poszukiwania reguł pozwalających oceniać stabilność układu bez obliczania pierwiastków równania charakterystycznego. Reguły te nazwano kryteriami stabilności. Kryteria te można podzielić na:
kryteria analityczne (Hurnitra, Routha),
kryteria grafo - analityczne (Michajłowa),
kryteria graficzne (Nyguista).
Kryteria analityczne i grafo - analityczne wymagają znajomości transmitancji.
Kryteria graficzne oparte są na charakterystyce częstotliwościowej i pozwalają oceniać stabilność układu regulacji bez znajomości jego równania charakterystycznego.
O kształcie charakterystyk częstotliwościowych układu regulacji decydują parametry regulatora i obiektu. Parametrowi obiektu regulacji zmieniać nie można, ale można zastosować odpowiedni regulator. Przypuśćmy, że na układ otwarty działa skok jednostkowy ε(t) i uzyskuje się odpowiedź y(t).
Układ niestabilny można ustabilizować zmieniając wartość transmitancji układu k0 regulatora oraz czas odpowiedni skokowej t1 i t2.
Zmieniając wzmocnienia k0 jest skuteczne ale niekorzystne, gdyż zmniejsza się dokładność regulacji i pogarsza dynamika procesu regulacji.
Można zmniejszyć t1, a więc zmniejszyć opóźnienie przebiegu y(t) układu otwartego, lub t2 a więc zwiększyć czas narastania funkcji y(t) układu otwartego.
WYKŁAD 8
Ocena jakości regulacji na podstawie odpowiedzi na zakłócenie skokowe
Problemy regulacji wiążą się również z zagadnieniem jakości regulacji. Chodzi o to aby układ regulowany miał stabilne parametry regulacji o określonych poziomach. Innymi słowy, wartość stanu wyjścia układu regulacji powinna być równa wartości zadanej „z” przy czym „z” może być liczba, wektorem lub funkcją.
W przypadku gdy wartość zadana „z” jest liczbą to taką regulację nazywamy stabilizacją, gdy „z” jest funkcją mamy doczynienia z pewnym rodzajem regulacji automatycznej nadążnym lub programowym.
Może się zdarzyć, że proces regulacji zmierza do stanu równowagi ![]()
, który różni się od wartości zadanej z. Różnicę między poziomem, osiągniętym przez układ już ustabilizowany a wielkością zadaną „z” nazywamy odchyleniem statycznym „ε”.
![]()
gdzie: ![]()
- wielkość stan równowagi,
z - wielkość zadana,
ε - odchylenie statyczne.
Sytuacje, w których w danym układzie powstaje odchylenie statyczne, w praktyce zdarzają się często. Mówimy wówczas, że działanie układu zawiera pewien błąd systematyczny. Istnieją dwie możliwości poprawy jakości regulacji:
zwiększyć zasilanie układu regulowanego S czyli sygnał sterujący „x”,
przebudować regulator „R” lub włączyć w układ dodatkowy regulator.
Innej możliwości nie ma gdy układ regulowany - obiekt „S” jest dany i jest to mieszkanie, termostat, chłodnica samochodowa i na jego budowę nie mamy wpływu. Obliczamy transmitancję - przepustowość regulatora R odpowiadającą zadanej wartości „z”. Wychodząc z podstawowego wzoru regulacji
![]()
przyjmujemy y = z,
otrzymujemy równanie:
![]()
.
Stąd znajdujemy
![]()
lub
|
(x) |
Z wzoru (x) wynika, że przepustowość regulatora w układzie stabilnym zależy od wielkości ![]()
, czyli od stosunku wielkości wejścia układu regulowanego - obiektu „S” x czyli zasilania układu do wielkości zadanej „z”.
Jeżeli w procesie regulacji występuje odchylenie statyczne należy przebudować regulator tak, aby jego przepustowość - transmitancja spełniała warunek ze wzoru (x). Z podstawowego wzoru regulacji wynika bezpośrednio, że wielkości zadanej y=z wielkość zasilania - sygnału wejściowego do układu regulowanego - obiektu „S” w układzie stabilnym musi być równa:
![]()
W praktyce sposób poprawienia działania procesu regulacji przez wielkość zasilania jest łatwiejszy i tańszy, chociaż często pozornie. Dla przykładu załóżmy, że przy pomocy odpowiedniego termostatu osiągnęliśmy układ stabilny przy czym poziom równowagi temperatury wynosi z=15[°C]. Natomiast chcemy osiągnąć temperaturę z=18[°C]. Zadanie można zrealizować:
przebudować regulator lub zastosować inny,
zmienić zasilanie układu regulowanego „S” dodając ustaloną na podstawie prób ilość paliwa lub, energii elektrycznej.
Ocena jakości (dobroci) regulacji polega na ustaleniu, który z regulatorów, możliwy w danym przypadku do zastosowania szybciej zlikwiduje zaburzenie. Jest to ważne gdyż w praktyce staramy się zastosować regulator sprawniejszy. Może powstać praktycznie zagadnienie, zastosowania regulatora realizującego stabilizację układu poprzez oscylację, czy też w sposób monotoniczny. Z tym łączy się zagadnienie, czy oscylacje prowadzące do stabilizacji układu mają mieć dużą ale szybko gasnącą amplitudę, czy też amplitudę gasnącą wolniej, ale za to mniejszą. Wszystkie te cechy stanowią o jakości układu regulacji.
Zadaniem więc każdego układu regulacji jest otrzymać równość między wartością wielkości regulowanej „y” i zadanej „z” czyli
![]()
Dokładnie spełniające tego warunku w układach rzeczywistych automatycznej regulacji jest niemożliwe. Różnica między wielkością regulowaną „y” a zadaną „z” nazwana jest uchybem regulacji
![]()
gdzie: ε - uchyb regulacji,
z - wielkość zadana,
y - wielkość regulowana.
Przyjmując dla uproszczenia z =0, otrzymamy:
![]()
.
Uchyb regulacji e(t) związany jest z sygnałem sterującym - zadanym z(t) i zakłócającym g(t) równaniami różniczkowymi.
Rozwiązaniem równań jest sumą całek
![]()
gdzie: eu - uchyb ustalony, odchyłka stateczna,
ep - uchyb przejściowy,
e - uchyb.
Uchyb przejściowy zmierz do zera, gdy czas zmierza do nieskończoności, jeśli wartość uchyb ustalonego równa jest zero; wtedy wielkość wyjściowa y→∞=z. Gdy natomiast eu≠0, to wielkość y→∞≠z. Kryteriami jakości regulacji działającymi na podstawie odpowiedzi na zakłócenie skokowe, są:
czas odpowiedzi t0,
czas regulacji tR,
przeregulowanie ℵ.
Czasem odpowiedzi t0 nazywamy czas okresu liczony od chwili zmiany sygnału sterującego do chwili, gdy odpowiedz skokowa układu osiągnie po raz pierwszy wartość zadaną (punkt A), co jest równoważne osiągnięciu przez uchyb regulacji po raz pierwszy wartości zerowej.
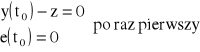
Czasem regulacji tR nazywamy okres czasu liczony od chwili zmiany sygnału sterującego do chwili, gdy odpowiedź skokowa osiągnie wartość zadaną w granicach ustalonej tolerancji ![]()
, co jest równoważne osiągnięciu przez uchyb regulacji stanu ustalonego z określoną dokładnością ![]()
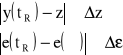
gdzie: ε(∞) - uchyb ustalony (odchyłka statyczna).
Przeregulowanie jest to, procentowy stosunek amplitud pierwszego przeregulowania e1 do drugiego przeregulowania e2
![]()
lub
![]()
gdzie: y1 - jest amplituda pierwszej oscylacji,
z - wartość zadana,
δ - maksymalny uchyb dynamiczny,
e1 - amplituda pierwszego odchylenia - przeregulowania,
e2 - amplituda drugiego odchylenia - przeregulowania.
Wielkości te zostały przedstawione w tabeli dla przebiegów aperiodycznych i oscylacyjnych. Wartości i kształt przebiegu przejściowego zależą od nastaw regulatorów które powinny gwarantować utrzymanie wymagań stawianych przebiegowi. Dążyć należy w zakresie przebiegu przejściowego do minimalnego czasu regulacji
tr = minimum
przeregulowanie
![]()
Wartości tych kryteriów wynikają a warunków technologicznych danego procesu, który podlega regulacji.
TABELA 1
rodzaj przebiegu |
Oddziaływanie skokowe na wejściu obiektu z(t)=zIJ(t) |
Oddziaływanie skokowe na wejściu układu ω(t)= ωIJ(t) |
||||||||
|
Układy z regulatorami astatycznymi |
Układy z regulatorami statycznymi |
Układy z regulatorami astatycznymi |
Układy z regulatorami statycznymi |
||||||
Aperiodyczny |
|
|
|
|
||||||
Oscylacyjny |
|
|
|
|
||||||
ε - uchyb regulacji |
||||||||||
1
71
Wyszukiwarka
Podobne podstrony:
Napęd Elektryczny wykład
wykład5
Psychologia wykład 1 Stres i radzenie sobie z nim zjazd B
Wykład 04
geriatria p pokarmowy wyklad materialy
ostre stany w alergologii wyklad 2003
WYKŁAD VII
Wykład 1, WPŁYW ŻYWIENIA NA ZDROWIE W RÓŻNYCH ETAPACH ŻYCIA CZŁOWIEKA
Zaburzenia nerwicowe wyklad
Szkol Wykład do Or
Strategie marketingowe prezentacje wykład
Wykład 6 2009 Użytkowanie obiektu
wyklad2
wykład 3
wyklad1 4
wyklad 5 PWSZ
więcej podobnych podstron