Mierniki współzależności między cechami jakościowymi.
Weryfikacja niezależności badanych cech statystycznych:
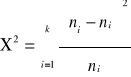
(r-1)(k-1) stopni swobody
gdy liczba stopni swobody > 30 do weryfikacji niezależności statystyka z:
![]()
Dopiero po odrzuceniu u hipotezy Ho można przystąpić do określenia siły związku między cechami za pomocą jednego z mierników korelacji.
współczynnik zbieżności T Czuprowa
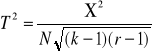
współczynnik kondygencji C Pearsona
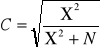
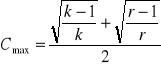
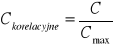
Jeżeli każda z cech jakościowych ma tylko 2 warianty do weryfikacji hipotezy o niezależności stochastycznej badanych cech stosujemy statystykę X2 o postaci:
![]()
Siły związku między badanymi cechami ustalamy za pomocą współczynnika zbieżności Pearsona:
![]()
, statystyka ta ma 1 stopień swobody.
Mierniki współzależności między cechami ilościowymi.
Współczynnik korelacji rang Spearmana
stosujemy, gdy N<30
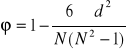
d - różnica między rangami
ϕ=0 - oznacza brak współzależności między badanymi cechami.
ϕ>0 - oznacza korelację dodatnią (wzrostowi jednej cechy towarzyszy wzrost drugiej).
ϕ<0 - oznacza korelację ujemną (wzrostowi jednej cechy towarzyszy spadek drugiej).
Wnioskowanie o współzależności w całej zbiorowości na podstawie współczynnika korelacji:
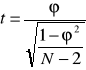
dla N<10 ![]()
dla N>= 10
Współczynnik korelacji liniowej Pearsona - r.
stosujemy, gdy N>30. Zależność między badanymi cechami jest liniowa
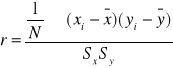
lub 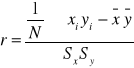
Weryfikacja:
![]()
N>=122 ![]()
N<122
Przedział ufności dla r-Pearsona w zbiorowości budujemy w oparci o następującą formułę:
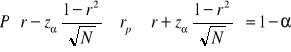
Wskaźniki (stosunki korelacyjne Pearsona)
Stosujemy, gdy N>=122, a zależność między badanymi cechami jest nieliniowa:
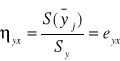
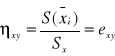
eyx=exy=r=0
eyx=exy=r=1
eyx=exy=r => kiedy zależność między badanymi cechami jest liniowa
Współczynnik korelacji r-Pearsona :
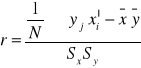
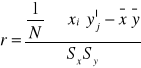
Weryfikacja istotności wskaźników korelacyjnych
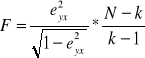
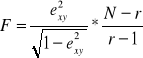
Kwadrat współczynników korelacji nazywamy współczynnikiem determinacji:
![]()
Rachunek regresji
![]()
![]()
![]()
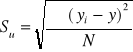
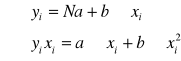
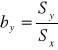
, ![]()
![]()
, ![]()
![]()
![]()
Miernikiem oceny dobroci otrzymanej funkcji regresji jest współczynnik rozbieżności φ2(fi):
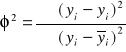
- informuje jaka część zmienności zmiennej zależnej nie jest wyjaśniana przez zmiany zmiennej niezależnej.
φ2=1-d2
Wnioskowanie statystyczne w rachunku regresji:
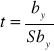
, Sby - błąd standardowy oceny danego parametru
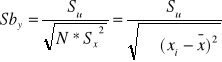
![]()
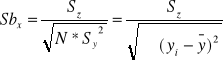
n-2 stopni swobody
Metody analizy dynamiki zjawisk
Przyrost absolutny o podstawie ruchomej.
PAr=yt-yt-1
PAs=yt-yto - o stałej podstawie (jednopodstawowy)
Indeksy (mierniki dynamiki)
![]()
![]()
Obliczanie przeciętnego tempa zmian badanego zjawiska:
![]()
![]()
Średnie tempo zmian:
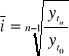
Szacowanie :
![]()
(procent składany)
Obliczania przeciętnego poziomu badanego zjawiska w szeregach czasowych momentów dokonujemy za pomocą średniej chronologicznej.
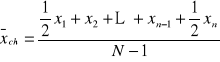
![]()
średnia 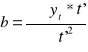
średnioroczny przyrost
![]()
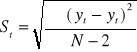
Wnioskowanie statystyczne przy funkcji trendu dotyczy
weryfikacji istotności współczynnika b w równaniu trend
![]()
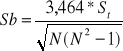
weryfikacji hipotezy dotyczącej losowości reszty dokonujemy w oparciu o nieparametryczny test serii:
![]()
![]()
![]()
k - liczba serii
n1=a z tablic odczytujemy k1
n2=b z tablic odczytujemy k2
![]()
hipotezy zerowej nie możemy odrzucić reszty mają charakter losowy. Liniowa funkcja trendu jest dobrą aproksymantą.
Wyszukiwarka
Podobne podstrony:
statystyka--Zarys statystyki wzory , Administracja
podstawy statystyki wzory id 36 Nieznany
Statystyka - podstawowe wzory, Statystyka wzory
statystyka - wzory 1 , 1
Statystyka wzory
statystyka wzory zadania duze
statystyka wzory 2
statystyka wzory kolokwium 2
statystyka wzory na egzamin zkw5xf4iosgbietwkpeub53rkm2z5feqn6kqp4y ZKW5XF4IOSGBIETWKPEUB53RKM2Z5F
Statystyka wzory, Wiedza, Statystyka
statystyka wzory na egz (do pomniejszenia) XXFM7CYZLD4IS5CATNHU2J5E2CYM4EXAKAMTZDI
statystyka wzory 0
STATYSTYKA - WZORY, Nauka, Ekonomia Finanse i Rachunkowość, Statystyka
Statystyka - wzory (tabelka), UE Katowice FiR, statystyka
Statystyka-wzory-2
statystyka wzory, Statystyka
statystyka wzory
Statystyka wzory duże
więcej podobnych podstron