Ćwiczenie nr 22

WYZNACZANIE SZYBKOŚCI HYDRATACJI BEZWODNIKA OCTOWEGO Z POMIARÓW PRZEWODNICTWA

Aparatura i szkło: Odczynniki:

Konduktometr, termostat, stoper, bezwodnik kwasu octowego

Kolbka miarowa o poj. 100 cm³,

Probówka o poj. 100 cm³

WYKONANIE ĆWICZENIA:

1. Ustawić termostat na temperaturę 20 ^oC (± 0,2 ^oC).

2. Przygotować zestaw do pomiaru przewodnictwa.

3. Do kolby miarowej wlać 12 cm³ bezwodnika octowego i uzupełnić wodą destylowaną do kreski. W momencie dodawania wody włączyć stoper i nie wyłączać aż do końca pomiarów (do ustalenia się wartości przewodnictwa). Rozpuszczać bezwodnik octowy w wodzie, silnie mieszając.

4. Wyznaczyć stoperem czas początku i końca rozcieńczania ( podczas dodawania wody pojawia się granica rozdziału dwóch faz, a po wstrząśnięciu, zmętnienie - - moment zniknięcia zmętnienia uznać za koniec rozcieńczania). Czas średni przyjąć za moment początku reakcji.

5. Naczynie (probówkę) z elektrodą umieścić w termostacie, wlać otrzymany roztwór i mierzyć przewodnictwo, początkowo częściej (trzy pomiary co 30 s, ok. 10 co 1 min), następnie jeden pomiar po upływie 5 min i jeden po 1 godz. (od początku reakcji). Stałość wskazań konduktometru oznacza koniec reakcji.

6. Wykonać analogiczne pomiary (punkty 2 - 5) w temperaturze 40 ^oC.

7. Wyniki zestawić w tabeli:

Nr	T [^oC]	Czas od początku reakcji, τ [s]			log( )	log	K

OPRACOWANIE WYNIKÓW:

Reakcja hydratacji bezwodnika octowego jest reakcją pierwszego rzędu, dlatego obliczenia należy przeprowadzić w oparciu o równanie:

k =
ln
=
ln
(1)

gdzie: c_o - początkowe stężenie bezwodnika octowego,

c_x - stężenie powstającego kwasu octowego,

τ - czas.

Wzrost przewodnictwa w czasie jest proporcjonalny do stężenie powstającego kwasu octowego. Ilość powstającego kwasu octowego proporcjonalna jest do ilości użytego bezwodnika octowego:

(CH₃CO)₂O + H₂O = 2CH₃COOH,

dlatego wzrost przewodnictwa w czasie trwania reakcji będzie proporcjonalny do początkowego stężenia kwasu octowego. Znając przewodnictwo roztworu w momencie początkowym κ_o , w danym momencie κ_τ i po czasie κ_∞ mamy:

c_o = const (κ_∞ - κ_o) (2)

(c_o - c_x) = const(κ_∞ - κ_o) - const(κ_τ - κ_o) = const(κ_∞ - κ_o - κ_∞ + κ_o) = const(κ_∞ - κ_τ),

gdzie: κ_o - przewodnictwo właściwe roztworu w momencie zainicjowania reakcji,

κ_o - przewodnictwo właściwe roztworu po upływie czasu τ,

κ_∞ - przewodnictwo właściwe po zakończeniu reakcji.

Z równań (1) i (2) wynika, że:

k =
ln
=
ln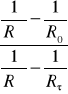
(3)

Przewodnictwo roztworu 1/R, w momencie rozpoczęcia reakcji, wyznacza się z ekstrapolacji zależności: ln(1/R_∞ - 1/R_τ) = f(τ). Dla reakcji pierwszego rzędu wykres takiej zależności jest linią prostą. Wyliczyć stałe szybkości dla każdego τ oraz obliczyć k_śr. i porównać jej wartość z wartością otrzymaną z wykresu (tangens kąta nachylenia prostej).

Znając wartości stałej szybkości w dwóch temperaturach, z równania:

ln
=
(
) (4)

obliczyć energię aktywacji E tej reakcji, a z równania:

k = A e^-E/RT (5)

obliczyć wartość stałej A.