1. Dany jest rosnący ciąg geometryczny, w którym
   

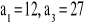
1. Wyznacz iloraz tego ciągu.

2. Zapisz wzór, na podstawie którego można obliczyć wyraz
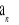
   dla każdej liczby naturalnej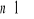
   .

3. Oblicz wyraz
   .

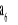
2. Iloraz ciągu geometrycznego (a_n) równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.

1. Oblicz pierwszy wyraz ciągu (a_n).

2. Podaj wzór na wyraz ogólny ciągu (a_n).

3. Sprawdź, czy ciąg o wyrazach 2, 6, 18, 36 jest geometryczny.

4. Wyznacz cztery początkowe wyrazy ciągu geometrycznego, jeśli: a₁ = 4, a₂ = 10.

5. Jaką liczbą musi być x, aby liczby: 6,x,54 tworzyły ciąg geometryczny?

6. Uzasadnij, że ciąg określony wzorem
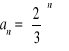
   jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.

7. Oblicz sumę S_n pierwszych n wyrazów ciągu geometrycznego, jeżeli a₁ = − 3, q = n = 4.

8. Oblicz sumę ośmiu początkowych wyrazów rosnącego ciągu geometrycznego, w którym a₁ = 4, a₃ = 16.

9. Dany jest rosnący ciąg geometryczny (a_n) dla n ≥ 1 , w którym a₁ = x , a₂ = 14 , a₃ = y . Oblicz x oraz y, jeżeli wiadomo, że x+ y = 35.

10. Liczby a, b, c, d są czterema kolejnymi wyrazami ciągu geometrycznego. Trzecia liczba jest o 9 większa od pierwszej, a druga liczba jest o 18 większa od czwartej. Wyznacz te liczby.

11. Wyznacz wszystkie wartości k
    R, dla których pierwiastki wielomianu W(x) = (x² − 8x + 12)(x − k) są trzema kolejnymi wyrazami rosnącego ciągu geometrycznego.

12. Ciąg (a_n) , dla n ≥ 1 jest ciągiem geometrycznym o ilorazie q =
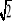
    . Oblicz wartość wyrażenia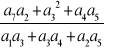
    .

13. W skończonym ciągu geometrycznym (a_n) wyraz pierwszy jest równy 3, a wyraz ostatni 768. Wiedząc, że suma wszystkich wyrazów wynosi 1533, oblicz iloraz tego ciągu.

14. Dla jakich x
    R \ {2} , liczby (x−2)² , x² − 4 , 2x² + 9x− 2 w podanej kolejności tworzą ciąg geometryczny? Dla znalezionej wartości x wyznacz ciąg i jego iloraz.

15. Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 26, różnica wyrazów czwartego i pierwszego wynosi 52. Oblicz piąty wyraz tego ciągu.

---