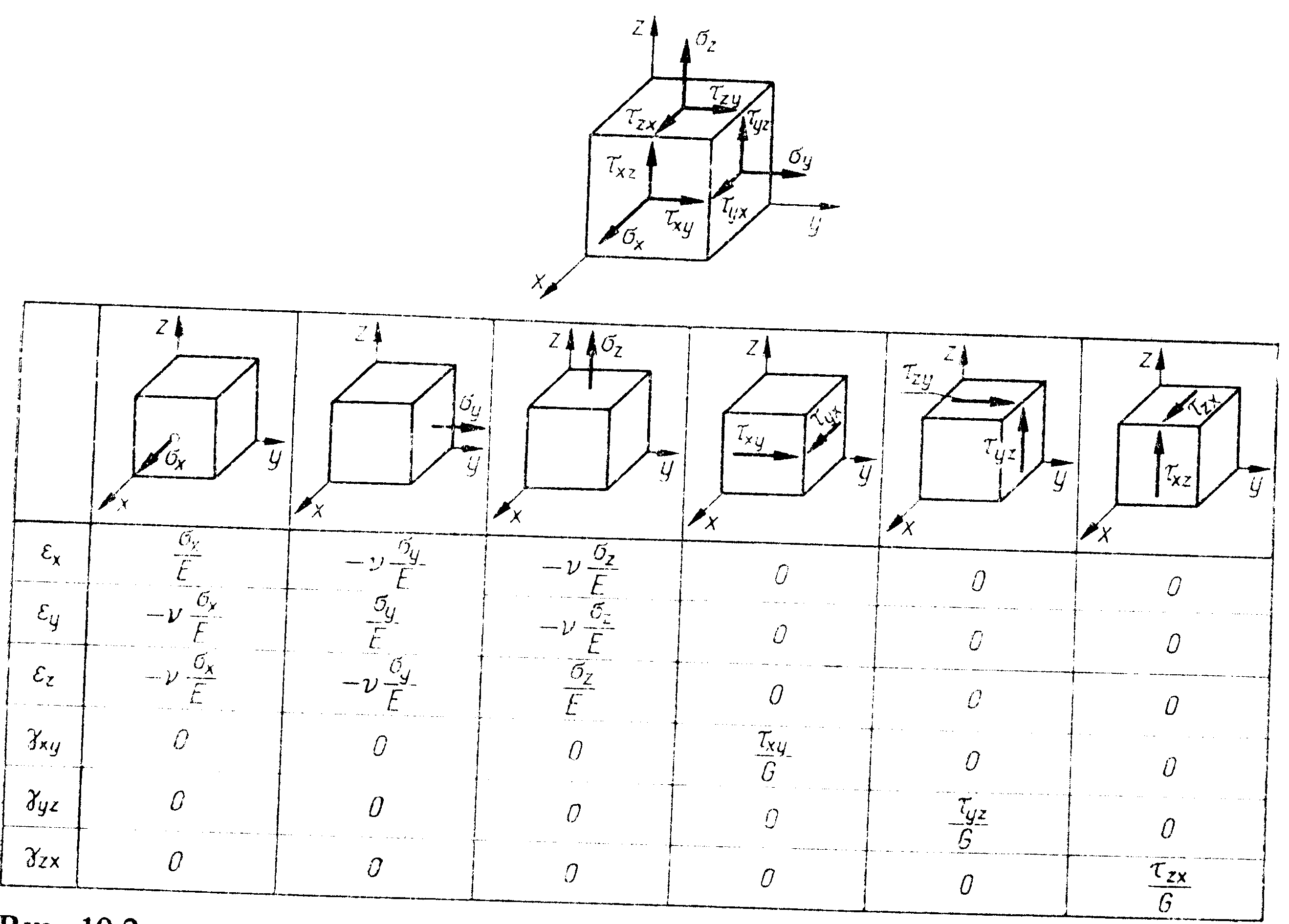
Dla materiału izotropowego

ε_x=1/E[σ_x-v(σ_y+σ_z)]; y_xy=τ_xy/G

ε_y=1/E[σ_y-v(σ_z+σ_x)]; y_yz=τ_yz/G

ε_z=1/E[σ_z-v(σ_x+σ_y)]; y_zx=τ_zx/G

Układ równań można rozwiązać, wyznaczając

naprężenia i otrzymuje się wówczas

σ_x=E/(1+ν)[ε_x+ν/(1-2ν)(ε_x+ε_y+ε_z)] τ_xy=Gy_xy

σ_y=E/(1+ν)[ε_y+ν/(1-2ν)(ε_x+ε_y+ε_z)] τ_yz=Gy_yz

σ_z=E/(1+ν)[ε_z+ν/(1-2ν)(ε_x+ε_y+ε_z)] τ_zx=Gy_zx

W zapisie skróconym wzory (10.3) i (10.4) przyjmują

następującą postać. e_ij=(1+v)/E σ_ij-v/Eσ_ααδ_ij

σ_ij=2Ge_ij+λe_ααδ_ijgdzie λ=2vG/(1-2v)-stałaLamego.

Wzory (10.3) i (10.4) lub (10.3a) i (10.4a) wyrażają

uogólnione prawo Hooke'a dla trójosiowego stanu

naprężenia w materiale izotropowym.

Składowe stanu odkształcenia (lub naprężenia)

są jednorodnymi liniowymi funkcjami składowych

stanu naprężenia (lub odkształcenia).

Zauważmy, że w przypadku gdy osie x, y, z są

głównymi osiami odkształcenia, to y_xy=0, y_yz=0,

y_zx=0;pociąga to jednak za sobąτ_xy=0,τ_yz=0,τ_zx=O

i dowodzi, że kierunki główne stanu odkształcenia

i stanu naprężenia w ciele izotropowym pokrywają

się. Dla płaskiego stanu naprężenia gdy σ_z=O,

τ_yz=O,τ_xz=O, zależności między składowymi stanu

naprężenia i odkształcenia wyrażają się następująco

ε_x=1/E(σ_x-vσ_y); ε_y=1/E(σ_y-vσ_x); y_xy=τ_xy/G

σ_x=E/(1-ν²)(ε_x+νε_y); σ_y=E/(1-ν²)(ε_y+νε_x); τ_xy=Gy_xy

---