Sekcja: II środa 14⁰⁰

Grupa: 5

Politechnika Śląska

Kierunek: MiBM

Wydział: Mechaniczny Technologiczny

rok ak. 2001/02

sem. letni

Katedra Wytrzymałości Materiałów

i Metod Komputerowych Mechaniki

LABORATORIUM WYTRZYMAŁOŚCI MATERIAŁÓW

Temat: STATYCZNA PRÓBA SKRĘCANIA METALI

Skład sekcji:

1.	Gorzeń Krzysztof
2.	Kopiec Damian
3.	Mura Marcin
4.	Rodź Marek
5.	Skuza Mateusz
6.	Sternal Łukasz
7.	Szymiczek Krzysztof
8.	Szymocha Mariusz
9.	Trzaskowski Marek
10.	Uliszak Szymon
11.	Watoła Piotr
12.	Wieczorek Michał
13.	Wojciechowski Grzegorz
14.
15.

1. Cel przeprowadzania statycznej próby skręcania

Przeprowadzenie statycznej próby skręcania ma na celu:

- pokazanie zachowania się materiału podczas próby;

- wyznaczenie pewnych wielkości charakteryzujących własności materiału (w naszym przypadku w

zakresie odkształceń sprężystych):

- sprawdzenie liniowej zależności kąta skręcenia Φ od momentu skręcającego M_S

- wyznaczenie modułu sprężystości poprzecznej G;

• statystyczne opracowanie wyników.

Jeżeli pręt jest obciążony w płaszczyźnie prostopadłej do jego osi parą sił o momencie K , to siły wewnętrzne zredukują się do momentu M_s, którego kierunek jest zgodny z osią pręta. Moment M_s nazywamy momentem skręcającym.

Odkształcenie (γ) Kąt skręcenia (ϕ) i rozkład naprężeń (τ_max) w pręcie skręcanym

Moment ten powoduje w poszczególnych przekrojach poprzecznych próbki płaski stan naprężenia i odpowiadający mu stan odkształcenia, który dla prętów o przekrojach kołowych w zakresie odkształceń sprężystych określany jest wzorami :

Τ_max =(Ms / W_o )

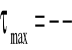
gdzie:

τ_max- największe naprężenia styczne

W_o - wskaźnik wytrzymałości na skręcanie

I_o - biegunowy moment bezwładności przekroju próbki

r - promień przekroju poprzecznego próbki

d_o - początkowa wartość próbki

gdzie:

ϕ - kąt skręcenia

l_o - długość pomiarowa próbki

GI_o - sztywność na skręcanie

G - moduł sprężystości poprzecznej

gdzie:

γ - kąt odkształcenia postaciowego (posunięcie)

Moduł sprężystości poprzecznej G wyznaczamy z równania :

W celu dokładniejszego określenia wartości G zastosujemy metodę statystyczną - metodę najmniejszych kwadratów, która jest jedną z częściej stosowanych metod do analizy wyników doświadczalnych. Jej ideą jest wyznaczanie takiej funkcji y = ƒ(x), która przy założeniu minimum błędu aproksymacji określa zależność pomiędzy otrzymanymi wynikami badań.

W naszym wypadku poszukujemy funkcję :

y = ax + b

gdzie:

y = Ms

x = ϕ

a = G [ Io / l_o ]

współczynniki “a” i “b” dobieramy tak aby suma kwadratów różnic pomiędzy wartościami doświadczalnymi y, a wartością oczekiwaną ax+b : należy dobrać „a” i „b” minimalizujące sumę :

wprowadzając oznaczenia :

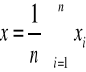
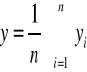
otrzymujemy rozwiązany układ równań w postaci :

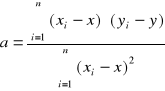
b = y - ax

Dla oceny dokładności pomiarów wyznaczamy wartość odchylenia standardowego:

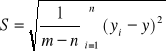
Wartości momentów M_prs, M_sps, M_es i M_ms zaznaczone na wykresie mogą posłużyć do wyznaczenia wartości granicznych naprężeń tj. odpowiednio: granicy proporcjonalności, sprężystości, plastyczności oraz wytrzymałości przy skręcaniu.

Wykres skręcania materiału sprężysto - plastycznego

Zaznaczyć tu należy, że próba skręcania lepiej obrazuje własności plastyczne materiału niż próba rozciągania. Wynika to z niezmienności wymiarów przekroju i długości próbki podczas skręcania aż do jej zniszczenia, co pozwala na określenie naprężeń w prze­kroju poprzecznym próbki nawet przy znacznych odkształceniach. W próbie rozciągania było to niemożliwe ze względu na tworzenie się tzw. szyjki.

Ujemną stroną próby skręcania jest nierównomierność rozkładu naprężeń w przekroju poprzecznym próbki, co znacznie komplikuje ujecie zjawiska powyżej granicy sprężystości w formę matematyczną - by uniknąć tego zjawiska stosuje się pręty cienkościenne.

Obliczenia:

Obliczeń dokonano w programie Microsoft Exel.

Obliczenie średniej średnicy pręta:

Średnica pręta
Lp.	Średnica pręta (d) [mm]	Wartość średnia (d) [mm]
1	17	17,01666667
2	17
3	17,1
4	16,9
5	17,1
6	17

Przeliczenie momentu skręcającego na [Nm]:

Lp.	Ms[kGm]	Ms[Nm]
1	0	0
2	3,1	30,411
3	6	58,86
4	9	88,29
5	12	117,72
6	15,1	148,131
7	18	176,58
8	21	206,01
9	24	235,44

Przeliczenie kąta skręcenia na [rad]:

L.p.	^	rad	^	rad	 rad
1	0	0	0	0	0
2	7,5	0,130833	3,5	0,061056	0,069778
3	10,5	0,183167	5	0,087222	0,095944
4	14	0,244222	7	0,122111	0,122111
5	17	0,296556	8,5	0,148278	0,148278
6	20,5	0,357611	10	0,174444	0,183167
7	23,5	0,409944	12	0,209333	0,200611
8	27	0,471	13,5	0,2355	0,2355
9	30,5	0,532056	15	0,261667	0,270389

Wykres w układzie Ms - ϕ

Obliczenie błędów oraz odchylenia standardowego dokonano w programach „MathCad” oraz „Analiza”

Metoda najmniejszych kwadratów została obliczona w programie „Analiza” Roberta Respondowskiegio

Odchylenie standardowe:

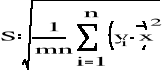
Wnioski:

---