Ćwiczenie 17

Pomiar strat ciepła w zależności od różnicy temperatur.

Przygotował: Michał Kruminia-Łozowski

Wydział: ETI

Kierunek: Automatyka-Robotyka inż.

Ogrzewane ciała tracą część swojej energii cieplnej i przekazują ją otoczeniu. W czasie podgrzewania część energii zamieniana jest na energię wewnętrzną, a część ulega wyemitowaniu do otoczenia. Im wyższa jest różnica temperatur podgrzewanego ciała i otoczenia tym większe są straty energii.

Bilans cieplny dla układu z ćwiczenia można zapisać w ten sposób:

Dla niedużych zmian temperatury q jest proporcjonalne do różnicy temperatur T (temperatura ciała) i To (temperatura otoczenia):

q=a(T-T0)

gdzie a jest współczynnikiem stałym dla danego materiału.

Oznaczając T-To jako t otrzymujemy wzór:

Rozwiązując równanie różniczkowe dla warunku początkowego, że w chwili temperatura ciała jest równa temperaturze zewnętrznego środowiska otrzymujemy teoretyczną zależność w postaci

Gdyby to temperatura osiągnęłaby graniczną wartość . W takim przypadku cała energia cieplna

zostaje oddana otoczeniu.

Zasada i przebieg pomiarów.

Badany układ składa się z naczynia metalowego wypełnionego wodą, w której zanurzone są: grzałka elektryczna, mieszadełko i sonda termometru. Do obwodu grzałki podłączony jest amperomierz i woltomierz. Moc grzałki jest regulowana napięciem wyjściowym.

W naszym doświadczeniu moc grzałki utrzymywana była na poziomie P = 26 W.

Oto otrzymane wyniki pomiarów:

Czas t [s]	Temperatura T [°C]	Temperatura [K]
0	19,2	292,3
120	19,8	292,9
240	20,4	293,5
360	21,0	294,1
480	21,6	294,7
600	22,0	295,1
720	22,6	295,7
840	23,2	296,3
960	23,6	296,7
1080	24,2	297,3
1200	24,6	297,7
1500	25,8	298,9
1800	27,0	300,1
2100	28,0	301,1
2400	29,0	302,1
2700	30,0	303,1
3000	30,8	303,9
3300	31,8	304,9
3600	32,6	305,7
3900	33,4	306,5
4200	34,0	307,1
4500	34,8	307,9
4800	35,4	308,5
5100	36,0	309,1
5400	36,6	309,7

Przez pierwsze 20 minut pomiary temperatury przeprowadzane były co dwie minuty, a następnie co 5. Pomiar temperaturu był przeprowadzony z dokładnością do 0,2 °C.

Na poniższym wykresie jest przedstawiona zależność dla wyników doświadzalnych.

W tabeli przedstawiono wartości przyrostu temperatury w czasie:

dt [min]	dT [°C]	dT/dt [°C/min]
2	0,6	0,3
2	0,6	0,3
2	0,6	0,3
2	0,6	0,3
2	0,4	0,2
2	0,6	0,3
2	0,6	0,3
2	0,4	0,2
2	0,6	0,3
2	0,4	0,2
5	1,2	0,24
5	1,2	0,24
5	1	0,2
5	1	0,2
5	1	0,2
5	0,8	0,16
5	1	0,2
5	0,8	0,16
5	0,8	0,16
5	0,6	0,12
5	0,8	0,16
5	0,6	0,12
5	0,6	0,12
5	0,6	0,12

Teoretyczny przebieg zależności otrzymujemy ze wzoru . Wartości wyznaczamy metodą najmniejszych kwadratów korzystając ze wzoru: , w którym:

Oto otrzymane wyniki:

a=-0,00018 [1/J]

b=0,00508 [K/J]

Znając możemy obliczyć temperaturę końcową tk, stałą a oraz pojemność cieplną układu K.

tk=320,9 [K] = 47,7 [°C]

stąd: K=5118,1 [J]

stąd: a=0,921 [1/K]

W poniższej tabeli podaję porównanie wyników teoretycznych z otrzymanymi doświadczalnie:

Czas t [s]	Temperatura-teoria [K]	Temperatura-doświadczenie [K]	Różnica
0	292,4	292,4	0,0
120	293,0	293,0	0,0
240	293,6	293,6	0,0
360	294,2	294,2	0,0
480	294,7	294,8	-0,1
600	295,3	295,2	0,1
720	295,8	295,8	0,0
840	296,4	296,4	0,0
960	296,9	296,8	0,1
1080	297,4	297,4	0,0
1200	297,9	297,8	0,1
1500	299,1	299,0	0,1
1800	300,2	300,2	0,0
2100	301,3	301,2	0,1
2400	302,3	302,2	0,1
2700	303,3	303,2	0,1
3000	304,2	304,0	0,2
3300	305,1	305,0	0,1
3600	305,9	305,8	0,1
3900	306,7	306,6	0,1
4200	307,4	307,2	0,2
4500	308,1	308,0	0,1
4800	308,8	308,6	0,2
5100	309,4	309,2	0,2
5400	310,0	309,8	0,2

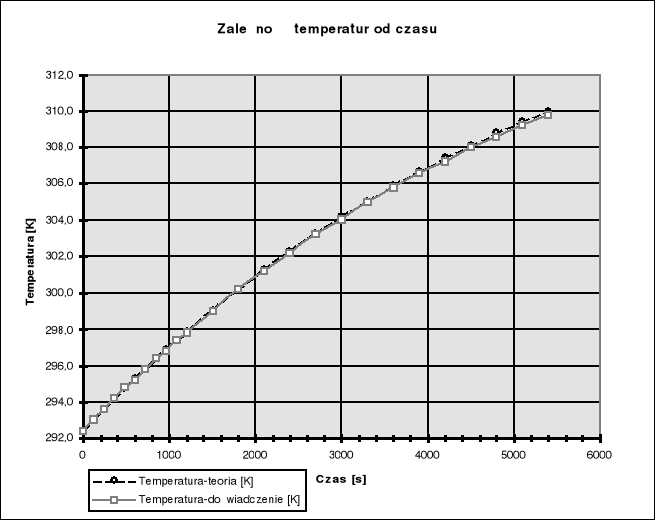
Jak widać z powyższego wykresu i tabeli zgodność wyników teoretycznych i doświadczalnych jest bardzo duża. Większą rozbieżność zaobserwować można w wyższych temperaturach.

Ćwiczenie 17

Pomiar strat ciepła w zależności od różnicy temperatur.

Przygotował: Wojciech Asztemborski

Wydział: ETI

Kierunek: Automatyka-Robotyka inż.

Ogrzewane ciała tracą część swojej energii cieplnej i przekazują ją otoczeniu. W czasie podgrzewania część energii zamieniana jest na energię wewnętrzną, a część ulega wyemitowaniu do otoczenia. Im wyższa jest różnica temperatur podgrzewanego ciała i otoczenia tym większe są straty energii.

Bilans cieplny dla układu z ćwiczenia można zapisać w ten sposób:

Dla niedużych zmian temperatury q jest proporcjonalne do różnicy temperatur T (temperatura ciała) i To (temperatura otoczenia):

q=a(T-T0)

gdzie a jest współczynnikiem stałym dla danego materiału.

Oznaczając T-To jako t otrzymujemy wzór:

Rozwiązując równanie różniczkowe dla warunku początkowego, że w chwili temperatura ciała jest równa temperaturze zewnętrznego środowiska otrzymujemy teoretyczną zależność w postaci

Gdyby to temperatura osiągnęłaby graniczną wartość . W takim przypadku cała energia cieplna

zostaje oddana otoczeniu.

Zasada i przebieg pomiarów.

Badany układ składa się z naczynia metalowego wypełnionego wodą, w której zanurzone są: grzałka elektryczna, mieszadełko i sonda termometru. Do obwodu grzałki podłączony jest amperomierz i woltomierz. Moc grzałki jest regulowana napięciem wyjściowym.

W naszym doświadczeniu moc grzałki utrzymywana była na poziomie P = 26 W.

Oto otrzymane wyniki pomiarów:

Czas t [s]	Temperatura T [°C]	Temperatura [K]
0	19,2	292,3
120	19,8	292,9
240	20,4	293,5
360	21,0	294,1
480	21,6	294,7
600	22,0	295,1
720	22,6	295,7
840	23,2	296,3
960	23,6	296,7
1080	24,2	297,3
1200	24,6	297,7
1500	25,8	298,9
1800	27,0	300,1
2100	28,0	301,1
2400	29,0	302,1
2700	30,0	303,1
3000	30,8	303,9
3300	31,8	304,9
3600	32,6	305,7
3900	33,4	306,5
4200	34,0	307,1
4500	34,8	307,9
4800	35,4	308,5
5100	36,0	309,1
5400	36,6	309,7

Przez pierwsze 20 minut pomiary temperatury przeprowadzane były co dwie minuty, a następnie co 5. Pomiar temperaturu był przeprowadzony z dokładnością do 0,2 °C.

Na poniższym wykresie jest przedstawiona zależność dla wyników doświadzalnych.

W tabeli przedstawiono wartości przyrostu temperatury w czasie:

dt [min]	dT [°C]	dT/dt [°C/min]
2	0,6	0,3
2	0,6	0,3
2	0,6	0,3
2	0,6	0,3
2	0,4	0,2
2	0,6	0,3
2	0,6	0,3
2	0,4	0,2
2	0,6	0,3
2	0,4	0,2
5	1,2	0,24
5	1,2	0,24
5	1	0,2
5	1	0,2
5	1	0,2
5	0,8	0,16
5	1	0,2
5	0,8	0,16
5	0,8	0,16
5	0,6	0,12
5	0,8	0,16
5	0,6	0,12
5	0,6	0,12
5	0,6	0,12

Teoretyczny przebieg zależności otrzymujemy ze wzoru . Wartości wyznaczamy metodą najmniejszych kwadratów korzystając ze wzoru: , w którym:

Oto otrzymane wyniki:

a=-0,00018 [1/J]

b=0,00508 [K/J]

Znając możemy obliczyć temperaturę końcową tk, stałą a oraz pojemność cieplną układu K.

tk=320,9 [K] = 47,7 [°C]

stąd: K=5118,1 [J]

stąd: a=0,921 [1/K]

W poniższej tabeli podaję porównanie wyników teoretycznych z otrzymanymi doświadczalnie:

Czas t [s]	Temperatura-teoria [K]	Temperatura-doświadczenie [K]	Różnica
0	292,4	292,4	0,0
120	293,0	293,0	0,0
240	293,6	293,6	0,0
360	294,2	294,2	0,0
480	294,7	294,8	-0,1
600	295,3	295,2	0,1
720	295,8	295,8	0,0
840	296,4	296,4	0,0
960	296,9	296,8	0,1
1080	297,4	297,4	0,0
1200	297,9	297,8	0,1
1500	299,1	299,0	0,1
1800	300,2	300,2	0,0
2100	301,3	301,2	0,1
2400	302,3	302,2	0,1
2700	303,3	303,2	0,1
3000	304,2	304,0	0,2
3300	305,1	305,0	0,1
3600	305,9	305,8	0,1
3900	306,7	306,6	0,1
4200	307,4	307,2	0,2
4500	308,1	308,0	0,1
4800	308,8	308,6	0,2
5100	309,4	309,2	0,2
5400	310,0	309,8	0,2

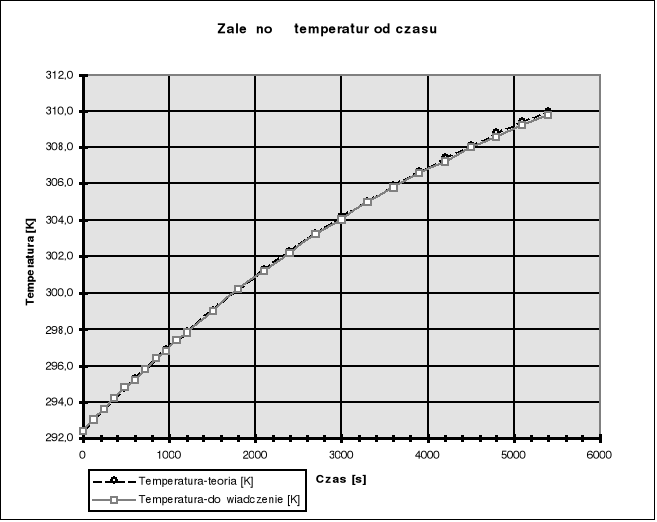
Jak widać z powyższego wykresu i tabeli zgodność wyników teoretycznych i doświadczalnych jest bardzo duża. Większą rozbieżność zaobserwować można w wyższych temperaturach.

---