Wstęp teoretyczny.
Siatką dyfrakcyjną nazywamy szereg szczelin umieszczonych w odległościach równych od siebie w nieprzezroczystym ekranie. Szczeliny otrzymuje się najczęściej przez porysowanie linii płasko-równoległej płytki szklanej szeregiem równoległych linii przy pomocy diamentu.
Zjawisko dyfrakcji - jeżeli na siatkę dyfrakcyjną, równoległa wiązka promieni pada prostopadle do jej powierzchni, wówczas każda szczelina staje się źródłem drgań i wysyła promienie we wszystkich kierunkach. Zjawisko to nazywamy inaczej uginaniem prostoliniowego biegu promieni.
Interferencja to inaczej nakładanie się na siebie fal świetlnych. Promienie mogą ze sobą interferować jeżeli różnice fal między promieniami zależą tylko od różnic dróg geometrycznych, a nie zależą od czasu. Biorąc pod uwagę wiązki promieni ugiętych zauważamy, że w pewnych kierunkach promienie te będą ulegały wzmocnieniu, a w innych będą wygaszały. Wzmocnienie promieni nastąpi wtedy, gdy różnice dwóch sąsiednich promieni będą różne całkowitej wielokrotności długości fali światła padającego.
Otrzymywanie widma za pomocą siatki dyfrakcyjnej.
Kąt wzmacniania się promieni ugiętych dla każdej długości fali oraz przy każdym rzędzie widma jest inny. Wynika stąd, że kierunki wzmacniania się promieni różnych barw są różne. Biorąc pod uwagę tę własność możemy zaobserwować następujące zjawisko: jeżeli poza siatką dyfrakcyjną, na którą pada wiązka promieni równoległych, umieścimy soczewkę zbierającą, a w pewnej odległości ekran, to wówczas powstaną na nim oprócz smugi odpowiadającej promieniom nieugiętym po jej obu stronach barwne widma, nazwane rzeczywistym. Jeżeli na miejscu soczewki umieścimy obserwatora, to soczewka oczna wytworzy na siatkówce obraz promieni ugiętych. Osoba patrząca wyobrazi sobie, że na przedłużeniu wiązek ugiętych znajdują się barwne źródła światła, mówimy wówczas o powstaniu widma pozornego.
Zasada pomiaru stałej siatki dyfrakcyjnej.
Stała siatki dyfrakcyjnej to odległość między rysami siatki mierzymy ją za pomocą mikroskopu wyposażonego w duży okular mikrometryczny. Stałą tą można wyznaczyć także przy pomocy światła o znanej długości fali. Korzystamy przy tym z następującego równania :
![]()
gdzie λ - długość fali
n - rząd widma
ϕn - średnia wartość kąta ugięcia
Jednak najdokładniejszym urządzeniem do wyznaczania kąta ugięcia promieni świetlnych jest spektrometr. Pomiar przy pomocy tego urządzenia wykonujemy w następujący sposób :
dokładnie regulujemy spektrometr
na stoliku spektrometru ustawiamy siatkę dyfrakcyjną prostopadle do biegu promieni świetlnych
ustawiamy krzyż nici pajęczej na środku prążka
znajdujemy położenie kątowe prążków 1..n na prawo i lewo
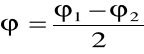
Mając dane położenie n-tego prążka na prawo i na lewo dokonujemy obliczenia średniej wartości kąta ugięcia korzystając z następującego wzoru :
Budowa spektrometru.
Spektrometr jest to urządzenie, które umożliwia dokładny pomiar kąta odchylenia promienia przez pryzmat lub inny układ optyczny. W zależności od konstrukcji spektrometr posiada części ruchome i nieruchome. W niektórych modelach nieruchome mogą być takie części, które w innym egzemplarzu są aktywne. Najczęściej można się spotkać ze spektrometrem, w którym kolimator i koło podziałowe są połączone na stałe z podstawą urządzenia. Natomiast stolik i luneta mogą się obracać naokoło tej samej osi, niezależnie od siebie. Niekiedy stolik oraz luneta mogą być unieruchomione względem koła podziałowego za pomocą dwóch śrubek zaciskowych. Aby uzyskać precyzyjne przesunięcia stolika i lunety używa się dwóch śrubek zwanych leniwkami. Luneta jest połączona z dwoma przesuniętymi względem siebie o 180o noniuszami, których podziałki znajdują się obok podziałek koła podziałowego. Światło wychodzące z monochromatycznego źródła (np. płomień sodowy, lampa rtęciowa lub neonowa) trafia na szczelinę o regulowanej szerokości i wchodzi do rury kolimatora. Szczelina znajduje się w płaszczyźnie ogniskowej soczewki umieszczonej na końcu kolimatora. Soczewka ta zmienia rozbieżną wiązkę promieni wychodzących ze szczeliny na wiązkę równoległą. Wiązka ta może następnie wchodzić do lunety bezpośrednio lub po odchyleniu przez pryzmat ustawiony na stoliku spektrometru. W płaszczyźnie poziomej umieszczone jest koło podziałowe z podziałką liczoną w stopniach. Oś koła jest przedłużeniem osi stolika.
soczewka
zbierająca
ekran
Otrzymywanie widma rzeczywistego Otrzymywanie widma pozornego
przy pomocy siatki dyfrakcyjnej przy pomocy siatki dyfrakcyjnej
KIERUNEK, W KTÓRYM
OBSERWATOR WIDZI POZORNE ŻRÓDŁO ŚWIATŁA
OKO
![]()
Wyszukiwarka
Podobne podstrony:
67-siatka dyfrakcyjna, sprawozdania, Fizyka - Labolatoria, Gotowe Spraw
Cw 09 - Wyznaczanie stałej siatki dyfrakcyjnej, Sprawozdania fizyka
siatka dyfrakcyjna, studia, Fizyka II
Siatka dyfrakc-teoria, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr67
Siatka dyfrakcyjna, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćw
,fizyka,siatka dyfrakcyjna
fizyka sprawozdania, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjne, Sprawozdanie z ćwi
fizyka sprawozdania, Pomiar długości fali świetlnej za pomocą siatki dyfrakcyjne, Sprawozdanie z ćwi
67-siatka dyfrakcyjna3, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria
siatka dyfrakcyjna, MIBM WIP PW, fizyka 2, sprawka fiza 2, fizyka lab, fizyka
siatka dyfrakcyjan, Materiały, Inżynieria Środowiska, Semestr 1, Fizyka
Pomiar stałej siatki dyfrakcyjnej za pomocą spektrometru (3), Sprawozdania - Fizyka
Siatka dyfrakc, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicze
sprawozdanie dyfrakcja bragga, Fizyka, Laboratoria, Sprawozdania, Sprawozdania cd, 1
fizyka siatka dyfrakcyjna
Opt- Pomiar stałej Siatki Dyfrakcyjnej za Pomocą Spektrometr, Sprawozdania - Fizyka
Siatka dyfrakcyjna 1, studia I i II stopnia, fizyka
Fizyka Siatka dyfrakcyjna
Lab. siatka dyfrakcyjna, Fizyka
więcej podobnych podstron