1.Wprowadzenie:
Siatka dyfrakcyjna jest to szereg wzajemnie równoległych i leżących w równych odstępach szczelin. Odległość między szczelinami nazywa się stałą siatki.
Spójna wiązka światła przechodząc przez dwie jednakowe szczeliny ulega ugięciu i daje dwie fale spójne interferujące ze sobą. Na ekranie umieszczonym w pewnej odległości od siatki możemy zaobserwować jasne i ciemne prążki interferencyjne. Maksima promieni ugiętych obserwuje się jako jasne paski. Następuje to wtedy, gdy między promieniami wychodzącymi z dwóch sąsiednich szczelin różnica dróg wynosi kl.
Siatki dyfrakcyjne dzielą się na transmisyjne i odbiciowe. Siatki transmisyjne można uzyskać przez nacięcie rys na szkle. Przerwy między rysami pełnią rolę szczelin. Inną metodą uzyskania siatek transmisyjnych jest metoda holograficzna. W siatkach odbiciowych rysy są nacinane na wypolerowanej powierzchni metalu, a światło padające na miejsca między rysami jest odbijane, dając taki sam rezultat końcowy jak światło przechodzące przez siatkę transmisyjną.
Innym ważnym podziałem siatek dyfrakcyjnych jest podział na siatki amplitudowe i fazowe. Siatką amplitudową nazywamy siatkę z nieprzezroczystymi obszarami przedzielającymi periodyczne obszary przezroczyste ( szczeliny ).Siatka fazowa w całym swoim obszarze jest przezroczysta dla światła, a odpowiednikami naprzemiennych obszarów przezroczystych i nieprzezroczystych są obszary
zmieniające periodycznie fazę fali świetlnej.
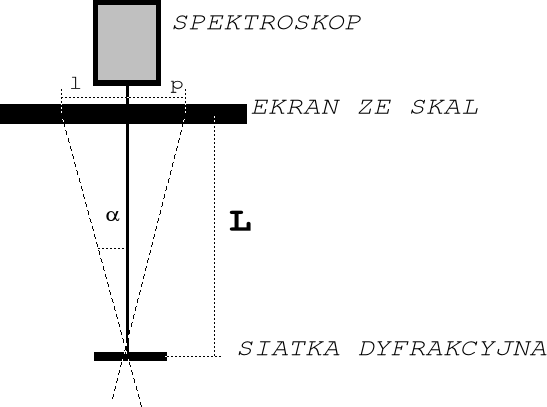
Rys. Budowa prostej aparatury do wyznaczenia stałej siatki dyfrakcyjnej.
L - odległość siatki od ekranu
l - odległość lewego prążka
p - odległość prawego prążka
a - kąt jaki tworzy kierunek promienia ugiętego z normalną do powierzchni siatki
Drugim parametrem, obok stałej siatki, jest kątowa dysperacja siatki. Jest to zdolność siatki do rozszczepiania światła polichromatycznego. Wyznacza się ją z zależności:
![]()
α - kąt jaki tworzy kierunek promienia ugiętego z normalną do powierzchni siatki
l - długość fali świetlnej
k - rząd maksimów dyfrakcyjnych
d - stała siatki
cos α - cosinus kąta kierunku promienia ugiętego
2. Tabela pomiarów:
Rodzaj |
Rząd |
Odległość prążka od szczeliny |
Odległość b [m] |
Długość |
||
|
|
na lewo a1 [m] |
na prawo |
średnia a0 [m] |
|
|
Sodowe |
1 |
0,078 |
0,077 |
0,0775 |
0,632 |
588,9 |
|
2 |
0,157 |
0,158 |
0,1575 |
|
|
Filtr 1 |
1 |
0,078 |
0,075 |
0,0765 |
|
576,55 |
|
2 |
0,152 |
0,153 |
0,1525 |
|
|
Filtr 2 |
1 |
0,054 |
0,057 |
0,0555 |
|
431,43 |
|
2 |
0,118 |
0,114 |
0,116 |
|
|
Filtr 3 |
1 |
0,071 |
0,068 |
0,0695 |
|
531,37 |
|
2 |
0,143 |
0,141 |
0,142 |
|
|
Filtr 4 |
1 |
0,085 |
0,082 |
0,0835 |
|
647,5 |
|
2 |
0,173 |
0,172 |
0,1725 |
|
|
3. Obliczenia:
Stałą siatki dyfrakcyjnej oblicza się ze wzoru
![]()
Aby wyznaczyć stałą siatki dyfrakcyjnej, należy wiązkę światła o znanej długości skierować prostopadle na siatkę dyfrakcyjną. Na ekranie po lewej i prawej stronie szczeliny obserwuje się prążki I i II rzędu . Mierzymy odległość prążków od szczeliny z lewej (a1) i prawej (a2) strony. Średnią odległości prążka od szczeliny (a0) obliczamy ze wzoru
![]()
Mierzymy również odległość ekran-siatka (b).
Wartość sinusa kąta ugięcia α wyznaczamy z zależności trygonometrycznych
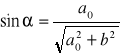
Korzystając z tej zależności stałą siatki dyfrakcyjnej obliczamy ze wzoru
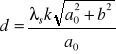
gdzie :
d - stała siatki dyfrakcyjnej
λs - średnia długość fali świetlnej przechodzącej przez siatkę
k - rząd widma
a0 - średnia odległość prążka od szczeliny
b - odległość ekran-siatka
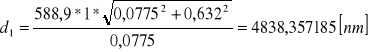
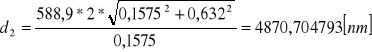
![]()
Długość fal świetlnych odpowiadających maksimum przepuszczalności filtrów obliczamy za wzoru
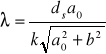
Filtr 1:
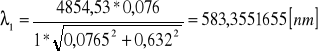
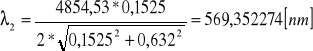
![]()
Filtr 2:
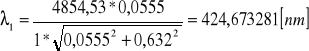
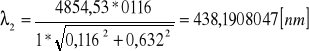
![]()
Filtr 3:
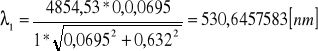
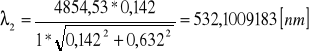
![]()
Filtr 4:
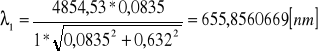
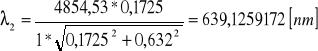
![]()
4.Rachunek i dyskusja niepewności pomiarowych:
Niepewność wzorcowania dla wielkości an i b wynosi odpowiednio
![]()
![]()
![]()
Niepewność eksperymentatora dla wielkości an i b wynosi odpowiednio
![]()
![]()
Całkowita niepewność pomiarowa wielkości a i b wynosi odpowiednio
![]()
![]()
Do obliczenia niepewności całkowitej wielkości d oraz λ korzysta się ze wzoru
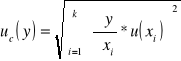
który po przekształceniu, dla wartości d ma postać
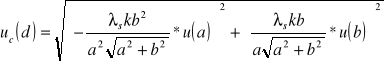
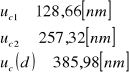
dla wartości λ
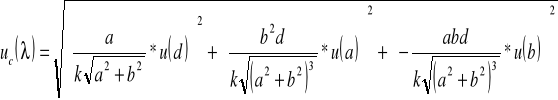
Do obliczenia uc(λ) przyjmujemy obliczoną wcześniej wartość u(d)=385,98.
Dla kolejnych filtrów uc(λ) przyjmuje różną wartość:
Filtr 1:
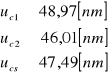
Filtr 2:
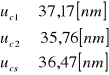
Filtr 3:
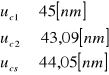
Filtr 4:
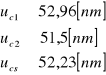
Średnia niepewność całkowita λ dla wszystkich filtrów wynosi
![]()
5.Wnioski:
Jak widać z doświadczenia każda długość fali świetlnej odpowiada odpowiedniemu widmu w odpowiedniej barwie tak np najdłuższej długości fali świetlnej odpowiada widmo koloru czerwonego natomiast przy najkrótszej fali obserwujemy widmo koloru fioletowego. Widmo światła białego posiada wszystkie kolory z czego można sądzić ,że w skład światła białego wchodzą fale o różnej długości fali. Doświadczenie było przeprowadzone dosyć dokładnie co potwierdzają otrzymane wyniki ,które są zbliżone do tych które podają tabele.
Wyznaczanie długości fali świetlnej
za pomocą siatki dyfrakcyjnej
- 5 -
Wyszukiwarka
Podobne podstrony:
Siatka dyfrakcyjna, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćw
67-siatka dyfrakcyjna3, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria
Siatka dyfrakc, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicze
Siatka dyfrakcyjna 1, studia I i II stopnia, fizyka
wyznaczanie dlugosci fal za pomoca siatki dyfrakcyjnej, studia, fizyka
67-siatka dyfrakcyjna, sprawozdania, Fizyka - Labolatoria, Gotowe Spraw
rura kundta, studia, Fizyka II
wheahstone, studia, Fizyka II
newton, studia, Fizyka II
Laser, studia, Fizyka II
Siatka Dyfrakcyjna, Sprawozdania - Fizyka
brylasztywna, studia, Fizyka II
sprezyna, studia, Fizyka II
grawitacja, studia, Fizyka II
temp krytyczna, TRANSPORT PWR, STUDIA, SEMESTR II, FIZYKA, fizyka-wyklad, zagadnienia opracowane, za
planck poprawka, studia, semestr II, SEMESTR 2 PRZYDATNE (od Klaudii), Od Górskiego, II semestr, Fiz
więcej podobnych podstron