- 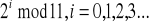
- 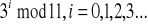
W pewnych momentach nie będzie trzeba liczyć przy wyższych liczbach i trzeba będzie zauważyc pewną zasadę.
A teraz przejdziemy do zadań. Załóżmy, że mamy alfabet afaniczny 26 literowy 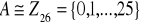
.
a b c d e f g h i j k l m n o p q r s t u v w x y z
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Załóżmy, że mamy ciąg dzisjestpieknapogoda. Będizemy go szyfrowac za pomocą szyfru przesuwającego o kluczu 11. Oto w jaki sposób się deszyfruje ciąg, a w jaki szyfruje:
Szyfrowanie: 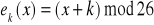
Deszyfracja: 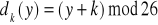
I kodujemy. Najpierw postać niezaszyfrowana:
d z i s j e s t p i e k n a p o g o d a
3 25 8 18 9 4 18 19 15 8 4 10 13 0 15 14 6 14 3 0
No i teraz ciąg zaszyfrowany. Szyfrować będziemy dodając do pozycji każdego znaku w alfabecie klucz modulo 26. I tak otrzymujemy:
a t p v y l a z r z o l o k t d u p d e
0 19 15 21 24 11 0 25 17 25 14 11 14 10 19 3 20 15 3 4
Zakodujmy jeszcze operując na tym samym alfabecie ciąg trendismyfriend korzystając z klucza 17. A więc najpierw postać niezakodowana:
t r e n d i s m y f r i e n d
19 17 4 13 3 8 18 12 24 5 17 8 4 13 3
No i teraz zakodujmy modulo 26 (bo alfabet 26 literowy od 0 do 25 pozycji):
k i v e u z j d p w i z v e u
10 8 21 4 20 25 9 3 15 22 8 25 21 4 20
A teraz taka zagadka. Załóżmy, że mamy taką postać zakodowaną. Pytanie: Jak rozszyfrować ten ciąg znaków nie znając klucza. Zasada jest taka, że najpierw zliczamy czestości liter występujących w zakodowanym słowie, a następnie bierzemy te litery najczęściej występujące i sprawdzamy, jaka jest ich odległość od siebie w alfabecie. Odległośc stanie się naszym kluczem i wtedy przesywamy w prawo o ten klucz i sprawdzamy, czy ciąg ma sens. Przykładowo litera e od litery i jest oddalona o 4. Za klucz przyjmujemy 4, ale po przesunięciu ciągu o 4 w lewo nic sensownego nie otrzymamy. Więc sprawdzamy odległość litery e od v. Jest 17, więc trafiliśmy. Zastosowanie tej metody wiąże się z duzym prawdopodobieństwem złamania takiego szyfru.
Na zakończenie jeszcze jedna praca domowa. Należy umieć liczyć algorytm euklidesa, czyli największy wspólny dzielnik jakichś duzych liczb. Przykładowo NWD(1236, 129). To nam się przyda na następne ćwiczenia.
![]()
![]()
![]()