Wydział ROLNICZY	Kierunek BIOTECHNOLOGIA		Grupa A1
Imię i nazwisko ROBERT BOROWIAK	Nr pary 7	Nr ewidencyjny 13	Prowadzący DR ELŻBIETA LEWANDOWSKA

14. Entalpia zobojętniania

Cel ćwiczenia

Zapoznanie się ze sposobem wyznaczania pojemności cieplnej kalory­metru oraz pomiaru entalpii rozpuszczania i zobojętniania.

Zasada pomiaru

Procesowi rozpuszczania krystalicznego NH₄Cl lub KCl w wodzie towa­rzyszy pewien efekt cieplny (ΔH), którego miarą może być zmiana tem­peratury układu (ΔT) zachodząca w czasie tej przemiany. Znając wartość molowej entalpii rozpuszczania tych związków oraz przyjmując zamiast rze­czywistej pojemności cieplnej (C) średnią pojemność cieplną w granicach temperatur T₁, T₂, można z następującej zależności wyznaczyć średnią po­jemność cieplną kalorymetru:

ponieważ

więc

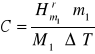
gdzie C - średnia pojemność cieplna kalorymetru,
- molowa entalpia rozpuszczania NH₄Cl lub KCl (kJ ∙ mol^-1), ml - liczba gramów substancji rozpuszczonej, m₁ - masa molowa substancji rozpuszczonej (g), ΔT₁ ­zmiana temperatury zachodząca w procesie rozpuszczania.

Przekształcając równanie do postaci:

można z niego obliczyć entalpię rozpuszczania dowolnej substancji (o masie molowej M₂), mierząc zmianę temperatury
podczas rozpuszczania m₂ gramów badanego związku w rozpuszczalniku (wodzie) o objętości takiej samej, jaka była stosowana. do wyznaczania średniej pojemności cieplnej kalorymetru (C).

Zmiana entalpii towarzysząca reakcji zobojętniania wodorotlenku sodu stężonym kwasem siarkowym (ΔH^c- entalpia całkowita) jest sumą entalpii rozpuszczania kwasu siarkowego (ΔH^r) i entalpii powstawania cząsteczek wody, czyli entalpii zobojętniania (ΔH^z):

stąd

Ponieważ w reakcji tej tworzą się dwie cząsteczki wody, więc

Ostatecznie otrzymujemy:

)

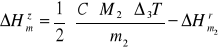
gdzie m₂ - liczba gramów kwasu siarkowego użytego do reakcji zobojęt­niania, M₂ - masa molowa kwasu siarkowego (g), C - średnia pojemność cieplna kalorymetru
- molowa entalpia rozpuszczania kwasu siar­kowego (kJ ∙ mol^-1) wyznaczona przez rozpusz­czenie takiej samej ilości kwasu, jakiej użyto do reakcji zobojętniania, tj. m₂.

Wykonanie ćwiczenia

1. Wyznaczenie pojemności cieplnej kalorymetru (kalibrowanie kalorymetru)

a. Odważyć w naczyńku wagowym około 5 g NH₄Cl lub KCl z dokładnością­ do 0,0001 g.

b. Do kalorymetru wlać 100 cm³ wody i mierzyć jej temperaturę w odstępach co 1 min w ciągu około 10 min (do czasu osiągnięcia niewielkich stałych zmian temperatury w kolejnych odczytach - okres wstępny).

c. Wsypać do kalorymetru odważoną ilość NH₄Cl lub KCl i ciągle mieszając mierzyć temperaturę przez pierwsze 5 min co 0,5 min, a następnie co 1 min przez około 30 min (do momentu, gdy zmiany temperatury będą niewielkie i stałe - okres główny i końcowy).

d. Otrzymane wyniki zestawić w tabeli I.

CZAS (MIN.)	OKRES POCZATKOWY
	1		2		3		4		5		6		7		8		9		10
TEMP. (ºC)
CZAS (MIN.)	OKRES GŁÓWNY
	10,5		11		11,5		12		12,5		13		13,5		14		14,5		15
TEMP. (ºC)
CZAS (MIN.)	OKRES KOŃCOWY
	16	17		18	19	20		21	22	23		24	25	26		27	28	29		30
TEMP. (ºC)

2. Wyznaczenie molowej entalpii rozpuszczania kwasu siarko­wego

a. Jak w punkcie l b.

b. Wprowadzić do kalorymetru 2 cm³ stężonego mierzyć zmiany temperatury jak w punkcie l c.

c. Wyniki wpisać do tabeli II.

CZAS (MIN.)	OKRES POCZATKOWY
	1		2		3		4		5		6		7		8		9		10
TEMP. (ºC)
CZAS (MIN.)	OKRES GŁÓWNY
	10,5		11		11,5		12		12,5		13		13,5		14		14,5		15
TEMP. (ºC)
CZAS (MIN.)	OKRES KOŃCOWY
	16	17		18	19	20		21	22	23		24	25	26		27	28	29		30
TEMP. (ºC)

3. Wyznaczenie molowej entalpii zobojętniania w reakcji wo­dorotlenku sodu z kwasem siarkowym

a.. W zlewce zawierającej 100 cm³ wody rozpuścić NaOH w ilości po­trzebnej do zobojętnienia 2 cm³ stężonego H₂S0₄. Roztwór ten oziębić do temperatury wody stosowanej w poprzednich pomiarach, tj. w punkcie lb i 2b.

b. Oziębiony roztwór NaOH przelać do kalorymetru i notować zmiany temperatury jak w punkcie lb.

c. Wprowadzić do kalorymetru 2 cm³ stężonego kwasu siarkowego i ciągle mieszając mierzyć temperaturę jak w punkcie lc.

d. Rezultaty pomiarów zebrać w tabeli III.

CZAS (MIN.)	OKRES POCZATKOWY
	1		2		3		4		5		6		7		8		9		10
TEMP. (ºC)
CZAS (MIN.)	OKRES GŁÓWNY
	10,5		11		11,5		12		12,5		13		13,5		14		14,5		15
TEMP. (ºC)
CZAS (MIN.)	OKRES KOŃCOWY
	16	17		18	19	20		21	22	23		24	25	26		27	28	29		30
TEMP. (ºC)

Sposób przedstawienia wyników

1. Pojemność cieplna kalorymetru

Substancja - NH₄Cl (KCl)

molowa entalpia rozpuszczania
- 15,99 (18,33) kJ ∙ mol^-1

masa substancji - m₁ =………………g

objętość wody - V= 100 cm³

zmiana temperatury -
= …………….°C

Sporządzić wykres zależności zmian temperatury układu od czasu. Wy­znaczyć metodą graficzną wartość
(patrz punkt 4.) i obliczyć pojemność cieplną kalorymetru (C.)

2. Wyznaczanie molowej entalpii rozpuszczania kwasu siarko­wego w wodzie

Sporządzić tabelę II na wzór tabeli I.

pojemność cieplna kalorymetru - C = ………………… kJ ∙ K^-1

masa H₂S0₄ (objętość 2 cm³) - m² =………………...g

objętość wody - V = 100 cm³

zmiana temperatury -
=…………………..°C

Wykreślić wykres zmian zależności temperatury od czasu i odczytać z niego
jak w punkcie 1. oraz obliczyć molową entalpię rozpuszczania H₂S0₄ (
).

3. Wyznaczanie molowej entalpii zobojętniania

Sporządzić tabelę III na wzór tabeli I i wykres zależności temperatury od czasu - T = ƒ(t).

pojemność cieplna kalorymetru - C =………… kJ ∙ K^-1

molowa entalpia rozpuszczania H₂S0₄ -
=………… kJ ∙ mol^-1

masa H₂S0₄ (o objętości 2 cm³) - m₂ = …………g

masa NaOH - m_NaOH =………….g

zmiana temperatury -
=………….°C

Na podstawie zależności obliczyć molową entalpię zobojętniania mocnego kwasu (H₂S0₄) mocną zasadą (NaOH). Wartość molowej entalpii rozpuszczania H₂S0₄ w tym równaniu bierzemy z pomiarów wykonanych w punkcie 2.

4. Wyznaczanie ΔT

Pomiar kalorymetryczny składa się, niezależnie od rodzaju kalorymetru, z trzech okresów: początkowego AB, głównego BC i końcowego CD (ryc.).

Okres początkowy trwa od rozpoczęcia obserwacji temperatury układu kalorymetrycznego do zainicjowania badanej przemiany. Od tego momentu do uzyskania maksymalnej temperatury trwa okres główny. Po nim zaczyna się okres końcowy, który trwa przez cały czas odczytywania pomiarów po okresie głównym. Jeśli nie byłoby wymiany ciepła z otoczeniem i innych do­datkowych efektów powodujących straty ciepła (układ idealnie izolowany), to temperatura w okresie początkowym i końcowym miałaby wartość stałą, a zmiana temperatury ΔT byłaby równa różnicy między nimi. Jednak z uwagi na to, że układ traci część ciepła na tzw. promieniowanie, zmierzona. w ka­lorymetrze różnica ΔT jest mniejsza od tej, jaką układ osiągnąłby, gdyby wy­równanie temperatur nastąpiło w bar­dzo krótkim czasie.

Aby wyeliminować błąd powstały na skutek wymiany ciepła z otocze­niem kreśli się tzw. krzywą idealnego wyrównania temperatur (ryc. 108), z której w drodze ekstrapolacji otrzy­muje się ΔT przy nieskończenie szyb­kim wyrównaniu temperatur. W tym celu nanosi się na wykres zmiany temperatury­

względem czasu - otrzymując krzywą ABCD. Następnie kreśli się prostą przechodzącą przez punkty pomiarowe odpowiadające okresowi początkowemu i przedłuża się ją w stronę wzrastających wartości czasu (na prawo od punktu B - krzywa I). Analogicznie kreśli się prostą przechodzącą przez punkty odpowiadające okresowi końcowemu i ekstrapoluje się ją w stronę przeciwną (na lewo od punktu C - krzywa II). Otrzymuje się w ten sposób dwie proste pomocnicze (I i II), lekko nachylone względem osi poziomej. Przedłużenia te łączymy prostą EF prostopadłą do osi czasu w ten sposób, aby odcinki EG i FG były równe. Odcinek EF wyznaczo­ny przez oba otrzymane w ten sposób punkty E i F odpowiada wartości ΔT = T₁ - T₀, otrzymanej przy nieskończenie szybkim wyrównaniu tempe­ratury. Wykres należy sporządzić bardzo starannie, ponieważ tylko wówczas wyznaczona wartość ΔT będzie w przybliżeniu równa wartości żądanej.

Ryc. Krzywa zmian tempera­tury układu w zależności od czasu: AB - okres wstępny, BC - okres

główny, CD - okres końcowy [6]

---