Katedra Fotogrametrii i Teledetekcji Olsztyn, dn. 31.03.2004r

UWM w Olsztynie

SPRAWOZDANIE NR 2

Temat ćwiczenia 3: FOTOGRAMETRYCZNA OCENA ZDJĘĆ LOTNICZYCH

Temat ćwiczenia 4: ANALITYCZNA ANALIZA POJEDYNCZEGO ZDJĘCIA

LOTNICZEGO

Wykonanie:

Anna Miszkiel

Monika Łach

Marta Malinowska

III GiSzN; II gr

ĆWICZENIE 3: FOTOGRAMETRYCZNA OCENA ZDJĘĆ LOTNICZYCH

Zdjęcia fotograficzne można podzielić na dwie postacie analogową i cyfrową. Podłoże tych zdjęć jest wykonane z płyt szklanych albo z filmów. Zdjęcia mogą być rejestrowane w zakresie IR, promieniowania widzialnego, czarno białym i wielospektralnym.

Analogowa postać zdjęcia to zdjęcie na pozytywie, diapozytywie i odbitki na papierze fotograficznym. Te trzy formy są dla zdjęć czarno-białych i barwnych. Istotne rzeczy na zdjęciu to: skala zdjęcia, która zależy od stałej kamery ck i wysokości fotografowania.

Przeglądane zdjęcia:

ODBITKA STRYKOWA NA PAPIERZE FOTOGRAFICZNYM

Odbitka inaczej pozytyw, powstaje przez naświetlanie papieru, na którym znajduje się negatyw. Nie jest to materiał do pomiaru. Służy do poglądów i robienia szkiców.

Pozytywy przechowywane są w kopertach we właściwym archiwum. W odpowiednich warunkach (naświetlenie, temperatura, klimatyzacja) Na każdej kopercie znajdują się informacje o : obiekcie, szeregu, nr zdjęć, ilości sztuk, skali. Na zdjęciach jest pieczątka, metryka, data, skala wykonani 1:13500, format 23 x 23.

CZARNO BIAŁE DIAPOZYTYWY

Robione kamerą RMB, ogniskowa 152 mm. Obraz cyfrowy wykorzystuje się do robienia pomiarów. Materiał niekurczliwy. Skala 1:6000 format 18 x 18. Materiał twardy lub ultra twardy dający zdjęcia o dobrym kontraście. Po prawej stronie diapozytywów znajdują się informacje o :liczniku ustawialnym na lotnisku, nr fabrycznym kamery, nr zdjęcia, stałej kamery. Na obrzeżach zdjęcia są punkty wzorcowe w formie małych prostokącików. Jest to sitka Reseau.

POKRYCIE PODŁUŻNE I POPRZECZNE

Zdjęcia lotnicze wykonane w celu opracowania mapy danego obszaru nazywane są zespołem zdjęć. W czasie jednego przelotu samolotu nad terenem przeznaczonym do sfotografowania kamera wykonuje w określonych odstępach czasu serię (szereg) zdjęć. Ponieważ jeden szereg zdjęć obejmuje pas terenu wzdłuż trasy lotu o szerokości równej bokowi kliszy w skali fotografowania, to w zależności od wielkości obiektu i skali zdjęć trzeba wykonać jeden, dwa lub więcej równoległych szeregów. Tak więc zespół zdjęć może się składać nawet z dużej liczby szeregów. Na przykład przy skali zdjęć 1:10000, wykonanych kamerą o formacie 23 cm, zostaje sfotografowany dla jednego szeregu pas terenu o szerokości 10000. 23 cm = 2300 m. Żeby między sąsiednimi zdjęciami w szeregu czy między szeregami nie było luk, zdjęcia są wykonywane tak, aby część obszaru odwzorowana na jednym zdjęciu była również odwzorowana na zdjęciach sąsiednich (zdjęcia muszą się pokrywać). Pokrywanie się zdjęć sąsiednich w jednym szeregu nazywane jest pokryciem w szeregu lub pokryciem podłużnym (P), zaś pokrywanie się zdjęć sąsiednich szeregów nazywane jest pokryciem w zespole lub pokryciem poprzecznym (q). Przy pokryciu n% odstęp między zdjęciami sąsiednimi wyniesie (100 - n)% boku kliszy. Na przykład przy pokryciu w szeregu wynoszącym 60% i formacie zdjęcia 23x23 cm odstęp między zdjęciami (baza fotografowania) wyniesie

b = (100-60). 23 cm = 0,40. 23 cm = 9,2 cm.

Przy skali zdjęć mz = 10000 baza ta w rzeczywistości wyniesie B = 10000 . 9,2 cm = 920m. Będzie to odstęp, w jakim zostaną wykonane kolejne zdjęcia podczas przelotu samolotu nad terenem.

Do opracowań stereoskopowych cały teren (obszar) jest fotografowany na parad zdjęć, czyli zdjęcia muszą mieć pokrycie podłużne wynoszące co najmniej 50%. W praktyce stosuje się najczęściej pokrycie podłużne około 60% oraz pokrycie poprzeczne około 30%. Do opracowań jednoobrazowych przyjmuje się p równe ok. 20%.

Wykonanie ćwiczenia:

Analizowano szereg 9 i 10. w szeregu 9 znajdują się zdjęcia od 617-636 a w szeregu 10 są zdjęcia od nr 642-654. każde zdjęcie ma metrykę i średnią skalę zdjęcia. W analizie szeregu 9 i 10 należy wyznaczyć pokrycie podłużne( dla 2D: p%=20-40% i poprzeczne-20%-30%.;3D p%=60-80%, q%=20%-40%;. Powierzchnię użyteczną fotogramu oblicza się z wzoru P_z = (L_x'y' M_z )²

1. W celu obliczenia pokrycia podłużnego (p%)

• 9 szeregu wzięto pod uwagę 3 pary zdjęć o numerach: 617 i 618, 626 i 627, 635 i 636.

p₁%=(13,7/22,6)*100%=60,6%

p₂%=(15,0/22,6)*100%=66,4%

p₃%=(12,0/22,6)*100%=53,1%

p_śr%=60%

• 10 szeregu wzięto pod uwagę 3 pary zdjęć o numerach: 642 i 643, 648 i 649,653 i654.

p₁%=(15,2/22,6)*100%=67,2%

p₂%=(13,8/22,6)*100%=61,1%

p₃%=(14,8/22,6)*100%=65,5%

p_śr%=65%

2. W celu obliczenia pokrycia poprzecznego (q%) szeregów 9 i 10 wzięto pod uwagę trzy pary zdjęć o numerach: 634 i 654, 628 i 648, 622 i 642

q₁%=(9,3/22,6)*100%=41,2%

q₂%=(9,7/22,6)*100%=42,9%

q₃%=(8,3/22,6)*100%=36,7%

q_śr%=40%

Kąt znosu szeregu

• szereg 9 tgα=4,5/40 → α=7,1320^g

• szereg 10 tgα= 0,5/30 → α=1,0609^g

Powierzchnia użyteczna pojedynczego fotogramu

P_z = (L_x'y' M_z )²

P_z = (22,6 x 5620 )²

P_z ≈ 161ha

ĆWICZENIE 4: ANALITYCZNA ANALIZA POJEDYNCZEGO ZDJĘCIA LOTNICZEGO

Układ współrzędnych tłowych jest prawoskrętnym ortogonalnym układem trój­wymiarowym. Początkiem układu jest środek rzutów (rys. 2.l), a płaszczyzna zdjęcia jest płaszczyzną x', y'. Przyjmuje się, że oś kamery jest prostopadła do płaszczyzny zdjęcia w punkcie głównym O' ( punkt przecięcia się osi kamery z płaszczyzną ramki tłowej ). Z tego względu, że w obiektywie, w którym znajduje się środek rzutu, nie ma ani kierunków odnie­sienia, ani fizycznych płaszczyzn odniesienia, trzeba przesunąć układ odniesienia do płaszczyzny zdjęcia. Układ znaczników tłowych zdjęcia określają osie x', y'. W układzie tym oś x' przyjmowana jest zazwyczaj wzdłuż osi lotu lub wzdłuż bazy, z której wykonano zdjęcia. Początek tego układu O', x', y', czyli położenie punktu głównego zdjęcia O' (rys. 2.l) można określić następująco: O' (x₀, y₀, O). Środek rzutu zdjęcia O znajdujący się w wewnętrznym punkcie głównym obiektywu (na osi kamery w odległości obrazowej Ck od płaszczyzny zdjęcia x', y') posiada natomiast w tym układzie współrzędne: O (x₀, y₀, Ck). Położenie jakiegokolwiek punktu A_i' na zdjęciu w tak zdefiniowanym układzie współrzędnych tłowych można określić współrzędnymi: A_i' (x_a, -y_a:, O)

Przyjmując za początek układu środek rzutów O, zdjęcie można rozpatrywać bądź w położeniu negatywowym (które odpowiada położeniu kamery w momencie fotografowania), bądź w położeniu pozytywowym (rys. 2.2).

Układ współrzędnych transformowanych

Układ współrzędnych transformowanych X_i', Y_i', Z_i' jest to układ, którego początek znajduje się w środku rzutów zdjęcia O, a osie są równoległe do osi lokal­nego układu współrzędnych terenowych X, Y, Z. Układ współrzędnych transformowanych różni się od układu przestrzennego współrzędnych jedynie orientacją. Ze względu na to, że osie kładu transformowanego są równoległe do osi układu terenowego X, Y, Z, nazywa się ten układ normalnym. Jeżeli kąty pomiędzy osiami układu transformowanego i układu zdjęcia są równe zeru, to układy pokrywają się ze sobą i tym samym odpowiednie współrzędne są sobie równe.

Orientację zdjęcia lotniczego w przestrzeni można podobnie jak w przypadku zdjęcia naziemnego, określić przez elementy kątowe, określające położenie osi kamery pomiarowej względem osi układu odniesienia oraz elementy liniowe (współrzędne geodezyjne), określające położenie środka rzutów w układzie odniesienia.

Położenie środka rzutów wyznaczają trzy współrzędne przestrzenne

Elementarni kątowymi są:

- kąt nachylenia zdjęcia v;

- kąt skręcenia zdjęcia κ, zawarty między linią największego spadku zdjęcia, a jedną z osi układu współrzędnych tłowych zdjęcia;

- kąt kierunkowy α głównej płaszczyzny pionowej zdjęcia, zawarty między główną płaszczyzną pionową zdjęcia, a płaszczyzną wyznaczoną przez osie układu współrzędnych - układu odniesienia X, Y.

Elementy orientacji wewnętrznej zdjęcia

Parametry orientacji:

• Stała kamery C_k

• Współrzędne punktu głównego: ∆x_o^', ∆y_o^'

• Dystorsje: radialna dr_r^', tangencjalna dr_tg^'

O^'- punkt główny

M^'- środek zdjęcia

X^', Y^'- osie płaskiego układu

współrzędnych tłowych zdjęcia

Elementy orientacji zewnętrznej zdjęcia (można obliczyć z warunku kolinearności lub z wykorzystaniem przekształceń rzutowych)

Parametry orientacji:

• Współrzędne środka rzutów w układzie terenowym x_o, y_o, z_o.

• Kąt nachylenia poprzecznego ω wokół osi X

• Kąt nachylenia podłużnego φ wokół osi Y

• Skręcenie zdjęcia κ

Wpływ nachylenia i deniwelacji terenu na przesunięcie punktów na zdjęciu

Nachylenie zdjęcia ma wpływ na jego skale. Rozpatrując skalę zdjęcia, jako stosunek długości odcinka l na zdjęciu do odpowiedniego odcinka L w terenie, można stwierdzić, że skala obrazu najszybciej zmienia się wzdłuż linii największego spadu- vv, a jest jednakowa wzdłuż linii poziomych prostopadłych do vv, ale różna dla każdej z nich ponieważ przy nachylonym zdjęciu każda z tych linii znajduje się na innej wysokości w stosunku do terenu i w związku z tym ma inną skalę.

Skala zdjęcia pionowego w terenie płaskim jest stała na całej powierzchni fotogramu.

Punkty zdjęcia nachylonego są przesunięte w stosunku do położenia tych punktów terenowych, które by się odfotografowały na zdjęciu wykonanym przy pionowym położeniu osi kamery. Przesunięcie to jest funkcją kąta nachylenia i zależy od położenia punktu na zdjęciu. Wartość tego przesunięcia można zapisać jako:

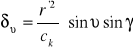
Przesunięcia punktów na zdjęciu lotniczym mogą być również spowodowane deniwelacjami terenu.

Jeżeli zdjęcie zostało wykonane kamerą o ogniskowej f (c_k) z wysokości W nad terenem, którego deniwelacje w stosunku do płaszczyzny odniesienia wynoszą ∆h, to wartość radialnego przesunięcia punktu P^' w stosunku do właściwego położenia jest równe:

Przesunięcie radialne punktu jest odwrotnie proporcjonalne do ogniskowej(c_k) i dlatego do opracowań sytuacyjnych metodą jednoobrazową wykonuje się zdjęcia kamerami o długich ogniskowych.

Zdjęcia prawie pionowe posiadają deformacje obrazu, które ograniczają ich kartometryczność. Dokładne mapy otrzymuje się dopiero w wyniku odpowiednich opracowań tych zdjęć.

Metryka kalibracji kamery

Kamera pomiarowa powinna być sprawdzana co jakiś czas, tak jak każdy inny instrument pomiarowy, w celu kontroli czy nie nastąpiła zmiana elementów orientacji wewnętrznej kamery, odpowiedzialnych za poprawną rekonstrukcję wiązki. Obywa się to w procesie tzw. kalibracji kamery. Kalibracja kamer fotogrametrycznych ma na celu wyznaczenie następujących elementów:

- stałej kamery (c_k),

- położenia punktu głównego w układzie łącznic znaczków tłowych (x₀, y₀),

- dystorsji obiektywu ( radialna i tangencjalna ),

- zdolności rozdzielczej obiektywu,

- współrzędnych znaczków tłowych

- odchylenia ramki tłowej od płaszczyzny

Dodatkowo, jeśli kamera zawiera siatkę reseau, określone powinny być również wspólrzędne siatki w układzie łącznic znaczków tłowych. Metody kalibracji kamer fotogrametrycznych dzielą się na laboratoryjne i polowe.

Metody laboratoryjne oparte są na wykorzystaniu kalibratorów wielokolimatorowych. Kalibrator składa się z dwóch, czterech lub większej liczby rzędów kolimatorów.

Metody polowe wymagają specjalnego pola testowego. W zależności od sprawdzanych elementów dobiera się odpowiednio rozmieszczone punkty pola testowego.

W przypadku kamer niemetrycznych elementy orientacji oraz ich stabilność bada się w procesie tzw. samokalibracji. Przez stabilność obrazu należy rozumieć jego powtarzalność geometryczną przy rejestracji nieruchomą kamerą bez zmiany ogniskowania. W aparatach cyfrowych rolę znaczków tłowych kamer fotogrametrycznych spełniają narożniki zdjęcia cyfrowego, względem których określa się położenie środka rzutów.

Elementy metryki kalibracji kamery Zeiss LMK:

• Schemat rozmieszczenia znaczków tłowych

• Współrzędne znaczków tłowych

• Emulsja

• Stała kamery

• Środek zdjęcia określony na podstawie przecięcia poziomej i pionowej łącznicy znaczków tłowych

• Środek zdjęcia określony w wyniku przecięcia diagonalnej znaczków tłowych

• Punkt PPS ( punkt główny symetrii )

• Punkt symetrii dystorsji radialnej

• Punkt PPA ( punkt główny autokolimacji )

• Kąt pod jakim przecinają się pionowa i pozioma łącznica

• Kąt pod jakim przecinają się diagonalne łącznice znaczków

• Dystorsja radialna i tangencjalna

• Odchylenie standarowe

• Błąd wyznaczenia współrzędnych znaczków tłowych

• Błąd wyznaczenia punktu PPA i PPS

• Odległość między znaczkami tłowymi

• Zdolność rozdzielcza

Określa się za pomocą:

• Kontrastu

• Emulsji

• Wywoływacza

• Gradacji

• Czasu i temperatury obróbki

• Rodzaj filmu jeśli był stosowany

• Średnie wartości fotograficznej zdolności rozdzielczej ( ilość linii na mm - 77 lini na mm )

• Odchylenie płyty dociskowej filmu od płaszczyzny

Wykonanie ćwiczenia:

Analiza pojedynczego zdjęcia lotniczego wykonanego na diapozytywie, o skali C_k = 152, 07.

DANE:

Anna Miszkiel Monika Łach Marta Malinowska

Nr zdjęcia: 638 639 648

Wysokość: 870 860 860

Odchylenie ν osi optycznej 1,5º 1,5º 2,0º

od linii pionu

Punkt główny O' na zdjęciu pomiarowym znajduje się na przecięciu linii łączących przeciwne znaczki tłowe, w stosunku do tego punktu określone jest położenie pozostałych punktów szczególnych:

Punkty:

• izocentryczny I'

• nadirowy N'

• zbiegu Z'

O'N'= tgν*C_K

O'Z'= ctgν*C_K

O'I'= tg(ν/2)*C_K

gdzie: c_k - stała kamery

ν- odchylenie osi optycznej od linii pionu

Anna Miszkiel Monika Łach Marta Malinowska

ON [ mm ] 3,98 3,98 5,31

OZ [ mm ] 5807,32 5807,32 4354,72

OI [ mm ] 1,99 1,99 2,66

Punkty te leżą na jednej prostej - linii największego spadu

Wydłużenie lub skrócenie promienia radialnego

dr'_ν=(r'²/c_k)*sinν*sinγ

dr'_ν-wartość przesunięcia punktu na zdjęciu spowodowana występowaniem kąta nachylenia ν

r'- promień radialny, odległość od początku układu współrzędnych do danego punktu P na zdjęciu

γ- kąt odłożony od linii największego spadku

Wpływ nachylenia zdjęcia na położenie punktów na zdjęciu:

c_k = 152,07

Anna Miszkiel Monika Łach Marta Malinowska

r'= 10 mm

v = 1^o56', 1^o54', 2^o05'

γ = 0^o → dr'_v = 0,00 0,00 0,00

r'= 10 mm

v = 6^o56', 6^o54', 7^o05'

γ = 0^o → dr'_v = 0,00 0,00 0,00

r'= 110 mm

v = 1^o56', 1^o54', 2^o05'

γ = 0^o → dr'_v = 0,00 0,00 0,00

r'= 110 mm

v = 6^o56', 6^o54', 7^o05'

γ = 0^o → dr'_v = 0,00 0,00 0,00

r'= 10 mm

v = 1^o56', 1^o54', 2^o05'

γ = 45^o → dr'_v = 0,02 0,02 0,02

r'= 10 mm

v = 6^o56', 6^o54', 7^o05'

γ = 45^o → dr'_v = 0,06 0,06 0,06

r'= 110 mm

v = 1^o56', 1^o54', 2^o05'

γ = 45^o → dr'_v = 1,90 1,90 2,04

r'= 110 mm

v = 6^o56', 6^o54', 7^o05'

γ = 45^o → dr'_v = 6,79 6,76 6,94

r'= 10 mm

v = 1^o56', 1^o54', 2^o05'

γ = 90^o → dr'_v = 0,02 0,02 0,02

r'= 10 mm

v = 6^o56', 6^o54', 7^o05'

γ = 90^o → dr'_v = 0,08 0,08 0,08

r'= 110 mm

v = 1^o56', 1^o54', 2^o05'

γ = 90^o → dr'_v = 2,68 2,64 2,89

r'= 110 mm

v = 6^o56', 6^o54', 7^o05'

γ = 90^o → dr'_v =,9,61 9,56 9,81

c_k = 305,00

r'= 10 mm

v = 1^o56', 1^o54', 2^o05'

γ = 0^o → dr'_v = 0,00 0,00 0,00

r'= 10 mm

v = 6^o56', 6^o54', 7^o05'

γ = 0^o → dr'_v = 0,00 0,00 0,00

r'= 110 mm

v = 1^o56', 1^o54', 2^o05'

γ = 0^o → dr'_v = 0,00 0,00 0,00

r'= 110 mm

v = 6^o56', 6^o54', 7^o05'

γ = 0^o → dr'_v = 0,00 0,00 0,00

r'= 10 mm

v = 1^o56', 1^o54', 2^o05'

γ = 45^o → dr'_v = 0,01 0,01 0,01

r'= 10 mm

v = 6^o56', 6^o54', 7^o05'

γ = 45^o → dr'_v = 0,03 0,03 0,03

r'= 110 mm

v = 1^o56'

γ = 45^o → dr'_v = 0,95 0,93 1,02

r'= 110 mm

v = 6^o56', 6^o54', 7^o05'

γ = 45^o → dr'_v = 3,39 3,37 3,46

r'= 10 mm

v = 1^o56', 1^o54', 2^o05'

γ = 90^o → dr'_v = 0,01 0,01 0,01

r'= 10 mm

v = 6^o56', 6^o54', 7^o05'

γ = 90^o → dr'_v = 0,04 0,04 0,04

r'= 110 mm

v = 1^o56', 1^o54', 2^o05'

γ = 90^o → dr'_v = 1,34 1,32 1,44

r'= 110 mm

v = 6^o56', 6^o54', 7^o05'

γ = 90^o → dr'_v = 4,79 4,77 4,89

Wraz ze wzrostem promienia radialnego r' i kąta γ rośnie wartość dr'

Im większe r^, ,tym zniekształcenie większe

Im większe C_k ,tym zniekształcenie mniejsze

Wpływ deniwelacji terenu na skalę zdjęcia:

dr'_Δh = (r΄ * Δh) / W

gdzie

Δh - deniwelacja terenu

W - wysokość fotografowania

W = 870 m

Δh [m] r' [mm]	10	50	100
r' = 10	0,11	0,17	1,15
r' = 110	1,26	6,32	12,64

W=860

Δh [m] r' [mm]	10	50	100
r' = 10	0,12	0,17	1,16
r' = 110	1,28	6,40	12,79

W=860

Δh [m] r' [mm]	10	50	100
r' = 10	0,12	0,17	1,16
r' = 110	1,28	6,40	12,79

Z powyższych obliczeń wynika. że dr'_Δh jest wprost proporcjonalne do deniwelacji terenu i promienia radialnego.

---