METODY ITERACYJNE:

funkcja iteracyjna

zależy od

np. dla metody Newtona:

dla metody siecznych:
m = 2

Metody iteracyjne 1 - punktowe:

m = 1

jeśli
jest ciągła to:

- punkt stały

czyli
jest pierwiastkiem równania:

Aby zbudować metodę iteracyjną rozwiązującą,
przekształcamy do postaci
.

Np. równanie:

Zbieżność - warunek dostateczny:

Założenia:

ma rozwiązanie
i w przedziale
istnieje pochodna
i
, wtedy dla każdego
:

a)

b)

c)
jest jedynym pierwiastkiem
leżącym w I.

Układy równań nieliniowych:

Przestrzeń n - wymiarowa

;

czyli:

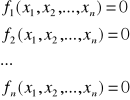
Metoda jednopunktowa:

;

;
k - numer iteracji

- numer współrzędnej wektora

oznaczmy:

Zbieżność metod iteracyjnych n - wymiarowych:

Załóżmy:
i że pochodna
dla

Istnieją dla

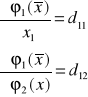
Warunek wystarczający zbieżności metody:

zachodzi:

macierz pochodnych cząstkowych

pochodna Frecheta

czyli, gdy
jest odwzorowaniem zwężającym (dla
)

< 1

Warunek konieczny zbieżności metody:

Warunkiem koniecznym zbieżności metody jest, aby promień spektralny macierzy
był nie większy od 1 (maksymalny moduł wartości własnych macierzy - promień spektralny).

Definicja pochodnej Frecheta:

Odwzorowanie
nazywamy różniczkowalnym w sensie Frecheta w punkcie
, jeśli istnieje taka macierz
, że

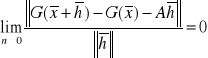
przy dowolnym sposobie wyboru wektorów
.

METODA NEWTONA:

Twierdzenie1: (o zbieżności lokalnej)

Niech
będzie różniczkowalna w sensie Frecheta w pewnym otoczeniu
punktu
, w którym
.

Załóżmy, że pochodna
jest ciągła w punkcie
, a pochodna
jest nieosobliwa. Wówczas punkt
jest punktem przyciągania metody iteracyjnej

zwanej metodą Newtona.

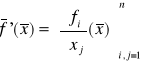
maksimum Jacobiego

nieosobliwa - zero jednokrotne

Algorytm:

1) oblicz

2) oblicz
(maksimum Jacobiego)

3) rozwiąż układ równań liniowych (oblicz
)

gdzie
(niedogodność)

4) podstaw

Kryterium zakończenia:

Zauważmy, że dla małych
zachodzi:

mała wyższego rzędu

Norma poprawki
może być, przy dość dużym k, dobrym przybliżeniem normy błędu
. Jej wzrost może sygnalizować osiągnięcie tzw. maksymalnej granicznej dokładności.

Algorytm iterujemy dopóki:

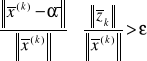
przyjęta dokładność

lub przerywamy, gdy:

gdzie
jest rzędu jedności

WIELOWYMIAROWA METODA SIECZNYCH:

- pierwiastek

Funkcję
przybliżamy odwzorowaniem afinicznym

i przyjmuję za przybliżenie
rozwiązanie pewnego układu równań
współczynniki maksymalne
i wektor
zależą od
oraz punktów
, dla których przybliżam funkcję.

przybliżam wielomianem
pierwszego stopnia.

Przybliżenie
definiuje się jako zero pewnego wielomianu
.

Postać wielomianu:

jest wielomianem interpolacyjnym.

Wartości
i W są takie same w n + 1 punktach.

dla
; k - nr iteracji

Dla wyznaczenia odwzorowania początkowego
należy znać wartość
w n +1 punktach początkowych
,
.

można zapisać w postaci:
,

a jego zero:
;

gdzie
i
są macierzami o kolumnach:

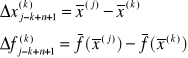
dla