Estymacja i weryfikacja liniowych jednorównaniowych modeli ekonometrycznych

Etapy badania ekonometrycznego

• Konstrukcja modelu

• Specyfikacja i kwantyfikacja zmiennych

• Zbieranie informacji statystycznych

• Estymacja parametrów

• Weryfikacja modelu

• Praktyczne wykorzystanie modelu

Modelowanie ekonometryczne - etapy:

I. Sformułowanie celu badania - cel badania oznacza sformułowanie teoretyczno-ekonomicznej hipotezy badanego zjawiska,

Np. sformułowanie teoretyczno-ekonomicznej hipotezy odnośnie kształtowania się popytu na dobro A

R_B - reklama dóbr substytucyjnych i komplementarnych

C_a - cena

C_B - cena dóbr substytucyjnych i komplementarnych

D - dochód

R_a - reklama naszego produktu

Inaczej mówiąc powyższy zapis oznacza, że popyt jest funkcją, czyli zależy od czynników, które uwzględniamy w nawiasie

• wpływ ceny na popyt zazwyczaj jest zgodny z ujemną korelacją tzn. wzrost ceny powoduje spadek popytu i odwrotnie. Powyższa relacja wypływa z prawa popytu, są od niej pewne wyjątki nazywane paradoksami ekonomicznymi (są trzy sytuacje kiedy wzrost ceny powoduje wzrost popytu)

• wpływ dochodów na popyt - korelacja dodatnia (w przypadku dóbr normalnych, wyższego rzędu) i korelacja ujemna (w przypadku dóbr niższego rzędu)

• trzykropek w powyższej hipotezie ekonomicznej reprezentuje w części te czynniki co składnik losowy w równaniu ekonometrycznym

II. Dane statystyczne : zbieranie informacji statystycznych i weryfikacja danych w przypadku tworzenia Banku Danych. Może się zdarzyć sytuacja, że z powyższej hipotezy ekonomicznej usuwamy niektóre zmienne objaśniające ze względu na brak danych statystycznych na ich temat.

III. Budowa modelu ekonometrycznego - polega na specyfikacji i kwantyfikacji zmiennych endogenicznych (objaśnianych) i egzogenicznych (objaśniających spoza analizowanego układu) oraz na wyborze postaci analitycznej równań stochastycznych.

IV. Estymacja modelu: znalezienie zgodnych, nieobciążonych i efektywnych ocen parametrów strukturalnych (współczynników stojących przy zmiennych objaśniających) oraz współczynników dopasowania i błędów średnich ocen parametrów (wartości sprawdzianu t-Studenta) i innych parametrów struktury stochastycznej oraz odpowiednich sprawdzianów testów

V. Weryfikacja modelu:

a) statystyczna - testowanie istotności ocen odpowiednich parametrów struktury stochastycznej

b) merytoryczna (ekonomiczna) - analiza sensowności ekonomicznej otrzymanych rezultatów (ocen parametrów strukturalnych)

VI. Testowanie modelu - ewentualnie respecyfikacja i reestymacja

VII. Praktyczne wykorzystanie modelu np. do prognozowania

EKONOMETRIA = ekonometria opisowa + badania operacyjne

Model ekonometryczny:

Matematyczny zapis prawidłowości ekonomicznych (dla empirycznej weryfikacji hipotez teorii ekonomii oraz dla zastosowań praktycznych - prognozowania)

Model ekonometryczny zawiera:

- równania

- nierówności

- funkcje

Typy relacji:

• behawioralne (zachowania się)

• technologiczne

• instytucjonalne (opisują sposób działania instytucji i regulacji prawnych)

• bilansowe (tożsamości)

W relacjach występują:

• zmienne (losowe lub nielosowe),

• parametry.

Relacje bilansowe pozwalają na uwzględnienie w badaniu, że suma tworzy zmienną zagregowaną. Występują w modelach wielorównaniowych.

Zmienne powinny być obserwowane. Wielkości które chcemy oszacować to zaś parametry modelu (tj. stałe współczynniki przy zmiennych) wyrażają one wpływ danej zmiennej na relację opisywaną w modelu (równaniu, funkcji).

Zmienne mogą być losowe i o wartościach z góry ustalonych (nielosowe + losowe z poprzednich okresów czyli „opóźnione”)

W badaniach operacyjnych mamy zmienne decyzyjne.

W ekonometrii opisowej są zmienne:

1. w modelu jednorównaniowym:

• objaśniana

• objaśniające

• składnik losowy

2. w modelu wielorównaniowym:

• endogeniczne (wewnętrzne)

• egzogeniczne (zewnętrzne)

• składniki losowe (czyli zmienne wyrażające wpływ wszystkich czynników pominiętych przy budowie modelu jak również wpływ zdarzeń czysto losowych - przypadkowych)

Inne klasyfikacje zmiennych (ze względu na ich rolę):

• sterujące,

• instrumentalne,

• z wyprzedzeniem czasowym,

• z opóźnieniem czasowym,

• zmienna czasowa (trend)

Zmienne:

- zerojedynkowe (1 - pojawia się cecha, 0 - jej brak)

- dyskretne - przyjmują liczby całkowite ale nie wszystkie

Zmienne zerojedynkowe mają zastosowanie do uchwycenia wpływu sezonowości lub periodyczności, mogą one także skwantyfikować wpływ złożonych zmiennych jakościowych poprzez dychotomizację.

np. w badaniu popytu na dane dobro chcemy uwzględnić wpływ wykształcenia jego uczestników. Dychotomizacja będzie polegała na utworzeniu 3 zmiennych zerojedynkowych:

Z1: 1 - podstawowe,

0 - w pozostałych przypadkach.

Z2: 1 - średnie,

0 - w pozostałych przypadkach.

Z3: 1 - wyższe,

0 - w pozostałych przypadkach.

Parametry w badaniach operacyjnych:

• współczynniki funkcji celu,

• współczynniki i wyrazy wolne w zbiorze warunków ograniczających.

Parametry w ekonometrii opisowej:

• strukturalne (współczynniki przy zmiennych),

• struktury stochastycznej (parametry rozkładu składnika losowego)

Klasyfikacja modeli w badaniach ekonomicznych - kryteria:

1. cel badania,

2. występowanie lub brak zmiennej losowej,

3. postać zależności,

4. liczba relacji,

5. znaczenie czasu,

6. zakres badania,

7. charakter powiązań pomiędzy zmiennymi endogenicznymi,

8. charakter poznawczy modelu.

Cel badania np. modele opisowe (do weryfikacji pewnych hipotez), modele służące do prognozowania (tzw. modele prognostyczne). Najlepiej jest gdy model ma charakter opisowo-prognostyczny. Stosowane są też modele służące do testowania własności estymatorów tzw. modele symulacyjne (w sensie technik symulacyjnych)

Można mówić o relacjach stochastycznych - to takie w jakich występuje zmienna losowa.

Relacje deterministyczne - brak losowości.

Postać zależności.

Wyróżnia się modele liniowe i nieliniowe. Modele liniowe to takie w których wszystkie relacje mają postać funkcji liniowej lub kombinacji liniowej. Modele nieliniowe to takie w których przynajmniej jedna relacja jest nieliniowa. Modele nieliniowe sprowadzalne są do postaci liniowej np. postać funkcji potęgowej, logarytmicznej, wykładniczej.

Liczba relacji:

• modele jednorównaniowe

• modele wieorównaniowe:

• modele proste - to takie, w których zmienne objaśniające są wyłącznie zmiennymi o wartościach z góry ustalonych tj. egzogeniczne + endogeniczne z poprzednich okresów,

• modele rekurencyjne - to takie, w których zmienne endogeniczne pełnią rolę zmiennych objaśniających, ale charakter powiązań pomiędzy nimi jest jednokierunkowy,

• modele o równaniach łącznie współzależnych - występują tu różnokierunkowe zależności między zmiennymi endogenicznymi tj. pojawiają się w takim modelu sprzężenia zwrotne, bezpośrednie lub pośrednie.

Znaczenie czasu. Możemy tu mówić o relacjach typu:

• dynamicznego (czas odgrywa tu rolę aktywną)

• statycznego

Aktywną rolę czasu uwzględnia się poprzez wprowadzenie zmiennych opóźniających egzo- i endo- , czasem też zmiennych antycypowanych oraz też zmiennej czasowej (dla uwzględnienia czynnika czasu).

Zakres badania. Wyróżnia się modele:

• mikroekonomiczne - dotyczące decyzji gospodarstwa domowego, funkcjonowania przedsiębiorstwa,

• makroekonomiczne - zakres badania obejmuje procesy i decyzje w skali krajowej / regionalnej.

Charakter poznawczy modelu może służyć do:

• opisu

• diagnozy

• prognozy

1. Charakterystyczną cechą modelu ekonometrycznego jest to, że nie jest on układem równań o dowolnych (lub przyjętych a priori) wartościach parametrów. Parametry te są wyznaczane z danych statystycznych.

2. Za oceny parametrów przyjmuje się takie liczby, przy których model jest możliwie dobrze dopasowany do zebranych danych statystycznych.

3. Kryteria zgodności modelu z danymi empirycznymi mogą być różnie zdefiniowane, co prowadzi do różnych metod estymacji.

4. Wybór metody estymacji zależy od:

• istniejących powiązań między nieopóźnionymi w czasie zmiennymi endogenicznymi,

• własności rozkładu składników losowych modelu.

5. W wyniku działania czynników losowych powodujących odchylenia, nie jest możliwe wyznaczenie liczbowych wartości parametrów dokładnie tzn. bez błędów.

Są to błędy szacunku (a nie błędy przeprowadzonych obliczeń).

6. Prawidłowy wybór metody estymacji pozwala jedynie na ograniczenie, lub wykluczenie systematycznych błędów oraz że wraz ze wzrostem liczby obserwacji prawdopodobieństwo popełnienia błędu maleje do zera.

7. Przy wykorzystaniu metod statystyki matematycznej można określić rząd dokładności szacunku parametrów.

MNK - jest najstarszą historycznie i intuicyjnie najprostszą metodą estymacji.

Jednorównaniowy model z jedną zmienną objaśniającą:

y_t = α_o + α₁x_t + ε_t (1)

y_t - zmienna objaśniana

α₀, α₁ - parametry modelu

x_t - zmienna objaśniająca

ε_t - składnik losowy

Założenia struktury stochastycznej składnika losowego:

1. składnik losowy ε_t ma wartość oczekiwaną równą zero:

E(ε_t) = 0

2. składnik losowy εt ma stałą (niezależną od wskaźnika t) wariancję σ2 o wartości skończonej

E(ε_t ²) = σ² [ D²(ε_t) = σ² - const]

3. obserwacje są niezależne, ciąg {ε_t} jest ciągiem niezależnych zmiennych losowych

E(ε_t, ε_t+s) = 0 [ cov (ε_t, ε_t+s) = 0]

Brak autokorelacji składnika losowego

4. Składnik losowy jest nieskorelowany ze zmiennymi objaśniającymi (lub zmienne objaśniające ze zmiennymi nielosowymi)

cov (ε_t,x_t) = 0

5. Składnik losowy na rozkład normalny

ε_t: N(0, σ²)

Zakładamy, że wykorzystana do estymacji próba losowa składa się z n obserwacji dokonanych na zmiennych y_t, x_1t, x_2t, ..., x_kt.

Estymacja parametrów polega na nadaniu im takich wartości liczbowych, przy których model (1) jest możliwie dobrze dopasowany do danych empirycznych.

Problem sprowadza się do tego, aby znaleźć takie a₀, a₁ aby prosta y = a_o + a₁x_t możliwie dobrze była dopasowana do punktów.

W MNK postuluje się aby był spełniony warunek::

Ψ = Σ(y_t - a₀ - a₁x_t)² = minimum (2)

MNK polega na znalezieniu takich ocen parametrów strukturalnych, przy których suma kwadratów odchyleń wartości empirycznych od wartości teoretycznych była jak najmniejsza.

Geometrycznie warunek (2) sprowadza się do tego by suma kwadratów odległości punktów od prostej na wykresie była jak najmniejsza.

Rozwiązaniem warunku (2) jest przy zastosowaniu rachunku różniczkowego znalezienie ekstremum funkcji dwóch zmiennych.

Wartości a₀ i a₁ znajdujemy rozwiązując układ równań:

a₁ Σx_t² + a₀ Σx_t = Σx_ty_t

a₁ Σx_t + na₀ = Σy_t

względem a₀ i a₁

a₀ = (Σy_tΣx_t² - Σx_tΣx_ty_t) /[nΣx_t² - (Σx_t )²]

a₁ = (nΣy_tx_t - Σx_tΣy_t) /[nΣx_t² - (Σx_t )²]

Błędy średnie szacunku parametrów α₀ i α₁ są odpowiednio równe:

D²(α₀) = σ² Σx_t² /n(Σx_t² - nx_śr²)

D²(α₁) = σ²/(Σx_t² - nx_śr²)

Przy przyjętych założeniach nieobciążoną oceną parametru σ² jest:

s² = Σ(Y_t - a₀ - a₁X_t)² /(n-2)

Klasyczna Metoda Najmniejszych Kwadratów

w zapisie macierzowym dla modelu liniowego z dowolną liczbą zmiennych

(KMNK)

Model jednorównaniowy o dowolnej liczbie zmiennych objaśniających:

y_t = Σ α_iX_it + ε_t lub Y=X α + ε (3)

Założenia:

1. Zmienne objaśniające x_1t, x_2t, ......., x_nt są wielkościami nielosowymi; zakładamy, ze nie występuje między tymi zmiennymi współliniowość.

2. Składnik losowy ε_t ma wartość oczekiwaną równą zero i stałą (nie zależną od wskaźnika t) wariancję σ², o wartości skończonej: E(ε_t) = 0

D²(ε_t) = σ²

3. Obserwacje są niezależne, tak że ciąg {ε_t} jest ciągiem niezależnych zmiennych losowych.

4. Składnik losowy ε_t jest nieskorelowany ze zmiennymi objaśniającymi.

Założenia techniczne stosowalności KMNK:

1. Zmienne x_i są nielosowe lub są zmiennymi losowymi o ustalonych wartościach.

2. n > k liczba obserwacji jest większa od liczby szacowanych parametrów.

3. Żadna ze zmiennych x_i nie jest liniową kombinacją innej zmiennej (żaden x_i nie jest silnie skorelowany z innymi x_i)

Zakładamy, że wykorzystana przy estymacji próba losowa składa się z n obserwacji dokonanych na zmiennych Y_t, X_1t, X_2t,........, X_1t.

- stałe współczynniki stające przy zmiennych są to parametry strukturalne, oznaczają one stopień albo siłę relacji zmiennej y na zmienną x.
można policzyć jako pochodną cząstkową y względem x.

- nie zmienia się w czasie, jest to stała, która mówi nam o ile zmieni się y_t jeśli x_it zmieni się o jednostkę.

zał. x_1t = 1

- wyraz wolny w modelu

Wyraz wolny pozwala nam na wyznaczenie y, jeśli wszystkie x przyjmą wartość zero. Geometrycznie to punkt przecięcia początku układu współrzędnych z płaszczyzną regresji.

wtedy parametrów mamy k+1

k - zmienna x

- składnik losowy modelu wyraża wpływ wszystkich czynników pominiętych w specyfikacji, ma on także wykryć pozostałe błędy wynikające z postaci analitycznej oraz ma wychwycić błędy wpływu wszystkich losowych zakłóceń = błędy czysto przypadkowe, losowe.

Pomiędzy y, a x - ami powinny być jak największe związki korelacyjne, a pomiędzy x-ami jak najmniejsze, a najlepiej ich brak.

Oznaczenia:

Y - wektor (n x 1) zaobserwowanych wartości zmiennej objaśnianej Y_t

X - macierz (n x k) zaobserwowanych wartości zmiennych objaśniających. Z uwagi na założenie (1) rząd tej macierzy jest równy k. Jeżeli występuje wyraz wolny, to jedna z kolumn jest kolumną samych jedynek

a - wektor (k x 1) ocen parametrów strukturalnych α_i

e - wektor (n x 1) reszt e_t równania

x₁₁ x₂₁ .. ... x_k1 y₁

x₁₂ x₂₂ .. ... x_k2 y₂

X = . . .. ... . Y = .

x_1n x_2n .. ... x_kn y_n

a₁ e₁

a₂ e₂

a = . e = .

. .

a_k e_n

Definicja.

Estymacja parametrów strukturalnych za pomocą MNK polega na znalezieniu takich wartości dla ich ocen, by suma kwadratów odchyleń rzeczywiście zaobserwowanych wartości zmiennej objaśnianej Y_t od ich wartości teoretycznych była jak najmniejsza.

Ψ = (Y - Xa)^T(Y - Xa) = minimum (4)

Y - Xa = e Ψ = e^Te

X^TX a = X^TY - układ równań normalnych

Twierdzenie I. Jeżeli macierz X jest rzędu k, wówczas Ψ przybiera wartość najmniejszą, gdy wektor a ocen parametrów strukturalnych modelu (3) dany jest wzorem:

a = (X^TX) ^-1 X^TY (5)

Estymator jest funkcją wyników z próby.

Przy założeniach 1 - 4 estymator (5) KMNK jest zgodny, nieobciążony i najbardziej efektywny, równoważny estymatorowi metody największej wiarygodności (MNW).

Estymator MNW wprowadza się poprzez maksymalizowanie przekształconej funkcji gęstości zmiennej losowej.

B - best

L - linear

U - unbalast

E - estimator

Oznaczenia:

α ₁ ε₁

α ₂ ε₂

α = . ε = .

. .

α _k ε_n

α - wektor (k x 1) prawdziwych wartości parametrów α_i

ε - wektor (n x 1) składników losowych ε_i

1) Zgodność

Obliczamy granicę prawdopodobieństw. Jeśli zwiększamy liczbą obserwacji to oceny będą coraz bardziej bliskie rzeczywistości.

2) Nieobciążoność E(a) = α

Polegająca na uwolnieniu się od systematycznych błędów szacunków.

3) Największa efektywność Var (a)
Var (a*)

Twierdzenie II. Jeżeli spełnione są założenia 1 - 4, to wyznaczone wzorem (5) estymatory parametrów strukturalnych modelu (3) są nieobciążone, to znaczy spełniają równość: E(a) = α

Dowód:

E(a) = E[(X^TX)^-1 X^TY], Y = X α + ε

E(a) = E[(X^TX)^-1 X^T(X α + ε)]

E(a) = E[(X^TX)^-1 X^TX α + (X^TX) ^-1 X^Tε)]

(X^TX) ^-1 X^TX = I, E(α) = α

E(a) = α +E[ (X^TX)^-1 X^Tε)]

E(a) = α

Twierdzenie III. Jeżeli spełnione są założenia 1 - 4, to macierz wariancji i kowariancji wyznaczonych relacją (5) estymatorów parametrów α_i modelu (3) dana jest wzorem:

D²(α) = σ²(X^TX)^-1 (6)

Macierz D²(α) ma wymiary (k x k). Elementy znajdujące się na jej głównej przekątnej są równe wariancjom poszczególnych parametrów, zaś znajdujące poza przekątną to kowariancje.

Przy przyjętych założeniach elementy macierzy D2(α) dążą do zera, gdy liczba obserwacji w próbie dąży do nieskończoności.

Ponieważ estymatory parametrów αi są nieobciążone, wynika stąd że są one zgodne.

lim P{|α - a| < ξ} = 1

n ->∞

gdzie: ξ - dowolnie mała liczba.

Twierdzenie IV. Jeżeli spełnione są warunki 1 - 5 i oceny parametrów strukturalnych modelu (3) dane są równaniem (5) to nieobciążoną oceną wariancji składnika losowego modelu jest wyrażenie:

s² = e^Te/(n-k), gdzie e = Y - Xa

s² = [Y^TY - Y^TX(X^TX)^-1X^TY]/(n-k)

Twierdzenie V. Jeżeli spełnione są założenia 1 - 5 i jeżeli składniki losowe ε_t mają rozkład normalny N(0, σ²), to estymatory parametrów α ₁, α ₂, ..., α _k modelu (3) mają k-wymiarowy rozkład normalny o wartościach oczekiwanych równych odpowiednio a₁, a₂,..., a_k i o macierzy wariancji i kowariancji danej wzorem (6).

Bierzemy pod uwagę liczbę stopni swobody zamiast liczbę obserwacji, dlatego że reszty maodelu sa wyznaczone dopiero po oszacowaniu k - parametrów strukturalnych.

Twierdzenie VI. Jeżeli spełnione są założenia tw.V i c_ii oznacza element stojący na przecięciu i-tego wiersza i i-tej kolumny macierzy (X'X)^-1 to zmienna losowa:

z = (a_i - α_i)/( σ c_ii )

ma rozkład normalny N(0,1), zaś zmienna losowa:

t = (a_i - α_i)/( s c_ii )

ma rozkład t-Studenta o n-k stopniach swobody.

Twierdzenie to może być wykorzystywane do budowy testów istotności dotyczących poszczególnych parametrów strukturalnych modelu.

Weryfikacja statystyczna rezultatów estymacji

Parametry struktury stochastycznej

Dla opisu stopnia zgodności modelu z danymi empirycznymi używa się:

1. wariancji resztowej oraz jej pierwiastka tj. odchylenia standardowego reszt

2. współczynnika zbieżności ϕ²

3. współczynnika determinacji R².

Współczynnik zbieżności mówi nam o udziale wariancji nieobjaśnionej w wariancji całkowitej. Współczynnik determinacji mówi o udziale wariancji objaśnionej w wariancji całkowitej.

R² = 1 - ϕ²

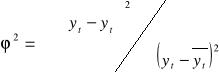
0 ≤ R² ≤ 1

R² = 1 ⇔ gdy wszystkie reszty y_t - y_t^* = 0 (brak odchyleń).

R² = 0 ⇔ gdy zmienne objaśniające modelu zostały dobrane w tak niewłaściwy sposób, że żadna z nich nie jest skorelowana ze zmienną objaśnianą.

Twierdzenie VII.

Przy założeniu, że Y_t ma rozkład normalny i jest nie skorelowane ze zmiennymi objaśniającymi (X₁, X₂, ...., X_k), rozkład zmiennej losowej R jest znany.

Zmienna losowa:

[R²/(k-1)] [(1- ϕ²)/(k-1)]

F = ----------------- = -----------------

[(1-R²)/(n-k)] [ϕ²/(n-k)]

ma rozkład Fishera-Snedecora o (k-1) i (n-k) stopniach swobody.

Korzystna sytuacja jeśli F obliczone jest większe od tabelarycznego.

Fakt ten może być wykorzystany do weryfikacji hipotezy H₀, że wszystkie parametry strukturalne (z wyjątkiem wyrazu wolnego) są równe zero. Zatem współczynnik determinacji R²=0.

Wyznaczanie błędów średnich ocen parametrów do testowania ich istotności.

s² jest nieobciążonym estymatorem wariancji modelu:

s² = e^Te/(n-k), gdzie e = Y - Xa
s² = [Y^TY - Y^TX(X^TX)^-1X^TY]/(n-k)

s =

s - błąd średni modelu

D²(α) = σ²(X^TX)^-1 =Ω- macierz wariancji i kowariancji

c_ii - element stojący na przecięciu i-tego wiersza i i-tej kolumny macierzy (X'X)^-1:

s(a₀) = s c₁₁

s(a₁) = s c₂₂

s(a₂) = s c₃₃ itd.

s(a_i) - błąd średni estymatora

Przedziały ufności

u = 1 - α

u - współczynnik ufności

α - poziom istotności

P[a_i - t_α s(a_i) < α_i < a_i + t_α s(a_i)] = u

t_α - wartość zmiennej o rozkładzie t-Studenta o n-k stopniach swobody, dla ustalonego współczynnika ufności.

Interpretacja.

Z prawdopodobieństwem równym „u” można stwierdzić, iż przedział <a_i - t_α s(a_i) ; a_i + t_α s(a_i)> pokrywa faktyczną wartość szacowanego parametru α_i .

Twierdzenie VI. Jeżeli spełnione są założenia tw.V i c_ii oznacza element stojący na przecięciu i-tego wiersza i i-tej kolumny macierzy (X'X)^-1 to zmienna losowa:

z = (a_i - α_i)/( σ c_ii )

ma rozkład normalny N(0,1), a zmienna losowa:

t = (a_i - α_i)/( s c_ii )

ma rozkład t-Studenta o n-k stopniach swobody.

Twierdzenie to może być wykorzystywane do budowy testów istotności dotyczących poszczególnych parametrów strukturalnych modelu.

W estymowanym liniowym modelu ekonometrycznym:

Y_t = Σ α_iX_it + ε_t

występują zmienne objaśniające, których wpływ na zmienną objaśnianą może być istotny lub nieistotny.

Istotności wpływu zmiennej „x_i” na zmienną „y” badamy weryfikując hipotezę:

H₀ : α_i = 0,

przy hipotezie alternatywnej:

H₁ : α_i ≠ 0.

Sprawdzianem hipotezy H₀ jest statystyka:

t(a_i) = a_i/s(a_i)

posiadająca rozkład t-Studenta o (n-k) stopniach swobody.

Obliczona wartość sprawdzianu jest porównywana z odczytaną z tablic wartością t_α , dla (n-k) stopni swobody i poziomu istotności α.

Jeżeli t(a_i) < t_α , nie ma podstaw do odrzucenia hipotezy H₀ . Oznacza to, iż nie jest wykluczone, że otrzymane oszacowanie a_i jest przypadkowe. Więc nie stwierdzono istotnego wpływu zmiennej x_i na zmienną objaśnianą y.

Jeżeli t(a_i) > t_α , odrzucamy hipotezę H₀ na korzyść hipotezy alternatywnej H₁. Oznacza to, że parametr α_i różni się istotnie od zera i obserwacje potwierdziły istnienie wpływu zmiennej x_i na zmienną objaśnianą y.

Przy około 20 obserwacjach i 2 szacowanych parametrach t_α tabelaryczne powinno być około 2 (α=0,05)

Uogólniona Metoda Najmniejszych Kwadratów

Założenia KMNK:

1. E(*t) = 0

2. D2(*t) = *2 - const.

3. E(*t, *t+s) = cov(*t, *t+s) = 0

4. E(Xt, *t) = cov(Xt, *t) = 0

5. *t: N(0, *2)

Z (2) i (3) * macierz wariancji-kowariamcji składnika losowego jest sferyczna (diagonalna o jednakowych elementach na głównej przekątnej):

Ω=
I

Uchylenie założenia 2.

heteroskedastyczność składnika losowego

Macierz wariancji i kowariancji składników losowych jest macierzą diagonalną, ale wariancje składników losowych nie są stałe:

σ₁² 0 0 . . . 0 c₁ 0 0. . . 0

0 σ₂² 0 . . . 0 0 c₂ 0. . . 0

E(εε') = . . . . . . . . = Π² . . . . . . . . . = Ω

0 0 0 . . . σ_n² 0 0 0 .. c_n

Uchylenie założenia 3.

Macierz wariancji i kowariancji składników losowych jest macierzą o stałych wariancjach, natomiast kowariancje składników losowych są różne od 0:

D²(ε_t) = σ² - constans

E(ε_t, ε_t+s) ≠ 0

1 ρ1 .... ρn-1

ρ1 1 .... ρn-2

ΩA = σ2 ... ... ....

ρn-1 ρn-2 .... 1

UMNK pomimo uchylenia założenia 2 lub 3 umożliwia otrzymanie estymatorów dobrych, tzn. zgodnych, nieobciążonych i najbardziej efektywnych.

UMNK polega na uwzględnieniu niesferycznej macierzy * (wariancji - kowariancji składnika losowego) w kryterium MNK:

Φ = (y-Xβ)'Ω(y-Xβ) = e'Ωe min

(kryterium Aitkena)

Z warunków koniecznych ekstremum (∂Φ/∂a=0):

b = (X'Ω-1X) -1 X'Ω-1Y

Alternatywnie UMNK polega na przekształceniu modelu wyjściowego

y=Xβ+ ε

przy zastosowaniu macierzy transformacji P do modelu:

Py = PXβ + P ε

co umożliwia spełnienie warunku 2:

D2(P ε) = σ2I

gdzie: Ω = (P'P)-1 <-> P'P = Ω -1

b=(X'P'PX) -1 X'P'Py = (X' Ω -1X) -1 X' Ω -1Y

D2(β) = σ2(X' Ω -1X)-1

Kroki praktycznej metody uogólnionej:

I. oszacowanie elementów macierzy Ω lub oszacowanie elementów macierzy transformacji P dokonuje się zazwyczaj na podstawie reszt z modułu oszacowanego klasyczną metodą najmniejszych kwadratów.

II. Wykorzystuje się oszacowanie
lub
dla wzoru b.

Stosowanie KMNK w tych przypadkach powoduje:

• utratę efektywności estymatorów parametrów strukturalnych, natomiast własności zgodności i nieobciążoności estymatorów parametrów strukturalnych zostają zachowane),

• utratę zgodności oraz nieobciążoności i efektywności parametrów struktury stochastycznej:

• estymatora wariancji resztowej,

• wariancji i kowariancji estymatorów parametrów strukturalnych (błędów średnich est.parametrów, statystyk t-Studenta),

• współczynnika zbieżności oraz

• współczynnika determinacji

Stosowanie standardowych testów istotności jest nieadekwatne.

Rezultaty (wnioski) mogą być obciążone i mylące.

UMNK umożliwia otrzymanie estymatorów dobrych, tzn. zgodnych, nieobciążonych i najbardziej efektywnych.

Idea UMNK polega na przekształceniu modelu wyjściowego do modelu:

PY = PXβ + Pε

D²(Pε) = σ²I (spełnienie warunku 2)

Ω = (P'P)^-1

β = (X'Ω^-1X) ^-1 X'Ω^-1Y

D²(β) = σ²(X'Ω^-1X)^-1

P - macierz transformacji

Dekompozycja składnika losowego.

Dekompozycja składnika losowego = analiza wariancji w statystyce

Zmienność zmiennej objaśnianej w modelu, mierzoną jej wariancją, można rozłożyć na części składowe:

1. część wytłumaczoną przez wpływ wyróżnionych w modelu zmiennych objaśniających,

2. część, która nie jest wytłumaczona przez działanie zmiennych objaśniających, a której wielkość jest funkcją wektora reszt.

s_y² = s_y*² + s²

s_y² - wariancja zmiennej Y

s_y*² - część wariancji zmiennej Y wytłumaczona przez X

s² - część wariancji zmiennej Y nie wytłumaczona przez X (wariancja resztowa)

s²_e = Σ(y_t - y_t^*)² s²_y = Σ(y_t - ysr_t)²

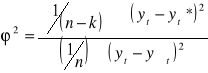
Współczynnik zbieżności ϕ² mówi o udziale wariancji odchyleń od modelu (reszt) w ogólnej wariancji zmiennej objaśnianej.

Badanie homoskedastyczności zakłóceń.

Homoskedastyczność = stałość składnika losowego

Heteroskedastyczność = różnicowanie wariancji

Przed zastosowaniem odpowiedniej procedury estymacji dla UMNK należy zastosować odpowiednie testy stwierdzające iż w modelu rzeczywiście istnieje homoskedastyczność albo autokorelacja składnika losowego.

Zgodnie z założeniem:

σ² = const.

Hipoteza zerowa:

H₀ : σ² = const.

Hipoteza alternatywna:

H₁ : σ² ≠ const.

W praktyce rozważamy trzy następujące sytuacje:

- wariancja zakłóceń wykazuje tendencje do zmian w czasie (wzrostu lub spadku),

- wariancja zakłóceń wykazuje tendencje do zmian, proporcjonalnie do zmian wartości zmiennej objaśnianej i/lub objaśniających,

- obserwacje w próbie pochodzą z kilku populacji różniących się wariancją zakłóceń.

Aby można było sformułować hipotezę alternatywną należy uporządkować obserwacje w próbie.

Test polega na oszacowaniu parametrów równani w dwóch podpróbach i zbadaniu czy wariancje zakłóceń różnią się istotnie w podpróbach.

Test Goldfelda-Quandta.

H₀: σ₁² = σ₂² = const.

H₁: σ₁² ≠ σ₂²

Jeśli prawdziwa jest hipoteza zerowa, wówczas stosunek wariancji reszt w podpróbach:

F = s₂²/s₁²

ma rozkład F Fishera-Snedecora z liczbą swobody równą odpowiednio stopniom swobody w pierwszej i drugiej podpróbie (jako drugą podpróbę wybiera się tę, w której wariancja reszt jest większa, aby stosunek F był większy od jedności).

Hipotezę zerową o homoskedastyczności zakłóceń odrzucamy, jeśli wartość sprawdzianu F przekroczy krytyczną wartość F_α, odczytaną z tablic dla wybranego poziomu istotności i odpowiednich stopni swobody.

- odrzucamy H₀

- brak podstaw do odrzucenia H_o

Inne testy: Breuscha-Pagana, White'a.

Jeżeli stwierdzimy heteroskedastyczność zakłóceń, z której wynika fakt, że estymator MNK nie jest efektywny, możemy na kilka sposobów szukać estymatora bardziej efektywnego:

1. Jeśli wariancja zakłóceń ma tendencje wzrostu w czasie, używamy ważonej metody najmniejszych kwadratów, będącej szczególnym przypadkiem UMNK.

2. Jeśli wariancja rośnie proporcjonalnie do kwadratu zmiennej objaśniającej X, można transformować model przez podzielenie równania stronami przez tą zmienną (jeśli zmienna transformowana ma sens ekonomiczny).

3. Zastosować UNMK po oszacownianiu odpowiednich elementów Ω.

4. Pozostać przy ocenach parametrów uzyskanych MNK, pamiętając, że nie jest to estymator efektywny oraz, że odpowiednie charakterystyki mogą być obciążone.

Badanie autokorelacji składnika losowego.

Przyczyny występowania autokorelacji składnika losowego:

1. Fakt dłuższego działania czynników przypadkowych, nie uwzględnionych w modelu.

2. Błędna budowa modelu:

- pominiecie jednej lub kilku istotnych zmiennych objaśniających,

- wprowadzenie do modelu zmiennej z niewłaściwym opóźnieniem czasowym,

- przyjęcie niewłaściwej postaci analitycznej modelu.

3. Autokorelacja zakłóceń, pojawiająca się bez ekonomicznie uzasadnionych przesłanek.

Najczęściej: Autokorelacja I rzędu

E(ၥ_t, ၥ_t-1) = ၲ (Ⴙ 0) czyli cov (ε_t, ε_t+1)
0

czyli

y = Xၢ + ၥ

ၥ_t = ၲ ၥ_t-1 + ၸ_t

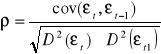
- parametr ten jest nieznany i trzeba go oszacować

Estymatory parametru ρ - współczynnika autokorelacji I rzędu:

a)

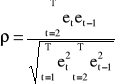
e - reszty MNK modelu liniowego y = x β + ε

b)

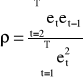
współczynnik autokorelacji reszt z próby (najczęściej używany)

c)

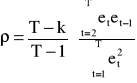
korekta relacji liczby stopni swobody do liczby obserwacji pomniejszonej o 1

d)

d - sprawdzian statystyki Durbina-Watsona

gdzie:

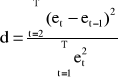
bowiem:

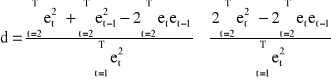
czyli:

Test Durbina - Watsona

(J.Durbin, G.S.Watson [1950]):

Statystyka d (DW):

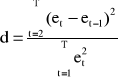
DW jest funkcją nie tylko sekwencji reszt, ale również pośrednio wartości wszystkich zmiennych objaśniających (elementów macierzy X)

Durbin i Watson określili empirycznie funkcję gęstości rozkładu zmiennej d i stwierdzili jej oscylacje pomiędzy dwoma granicznymi krzywymi f(d_i) i f(d_s) w zależności od liczby obserwacji T, liczby zmiennych objaśniających w modelu oraz od sekwencji reszt.

Krzywe te są symetryczne względem pionowej osi symetrii: d=2:

Z tego powodu tablice wartości krytycznych ułożone są ze względu na liczbę obserwacji i liczbę zmiennych objaśniających. Zawierają dwie wartości krytyczne:

d_L - dolną oraz d_U - górną

Proces wnioskowania (weryfikacji hipotezy dotyczącej istnienia autokorelacji składnika losowego modelu) pokazany jest na wykresie:

Procedura testowania:

1. Estymujemy dany model KMNK i obliczamy wektor reszt:

e_t = y_t - y_t*,

2. Obliczamy ocenę (r) współczynnika autokorelacji reszt (ρ):

Σ(e_te_t-1)²

r = ------------

Σ(e_t)²

3. Badamy istotność współczynnika autokorelacji r, weryfikując hipotezę

H₀: ρ = 0

przy jednej z hipotez alternatywnych:

a) H₁: ρ > 0, jeśli r jest dodatni,

b) H₁: ρ < 0, jeśli r jest ujemny,

Sprawdzianem dla tego układu hipotez jest statystyka d (DW).

Statystyka d ma rozkład empirycznie zbadany przez Durbina i Watsona (nazywany również rozkładem Durbina-Watsona), który jest stablicowany, a jej wartości krytyczne odczytujemy w zależności od liczebności próby n i liczby stopni swobody.

Przy danym poziomie istotności α z tablic rozkładu Durbina-Watsona odczytujemy dwie wartości krytyczne:

wartość dolną d_L i wartość górną d_U:

np.dla poziomu istotności 0,05; w zależności od liczby obserwacji i liczby zmiennych w modelu, mamy:

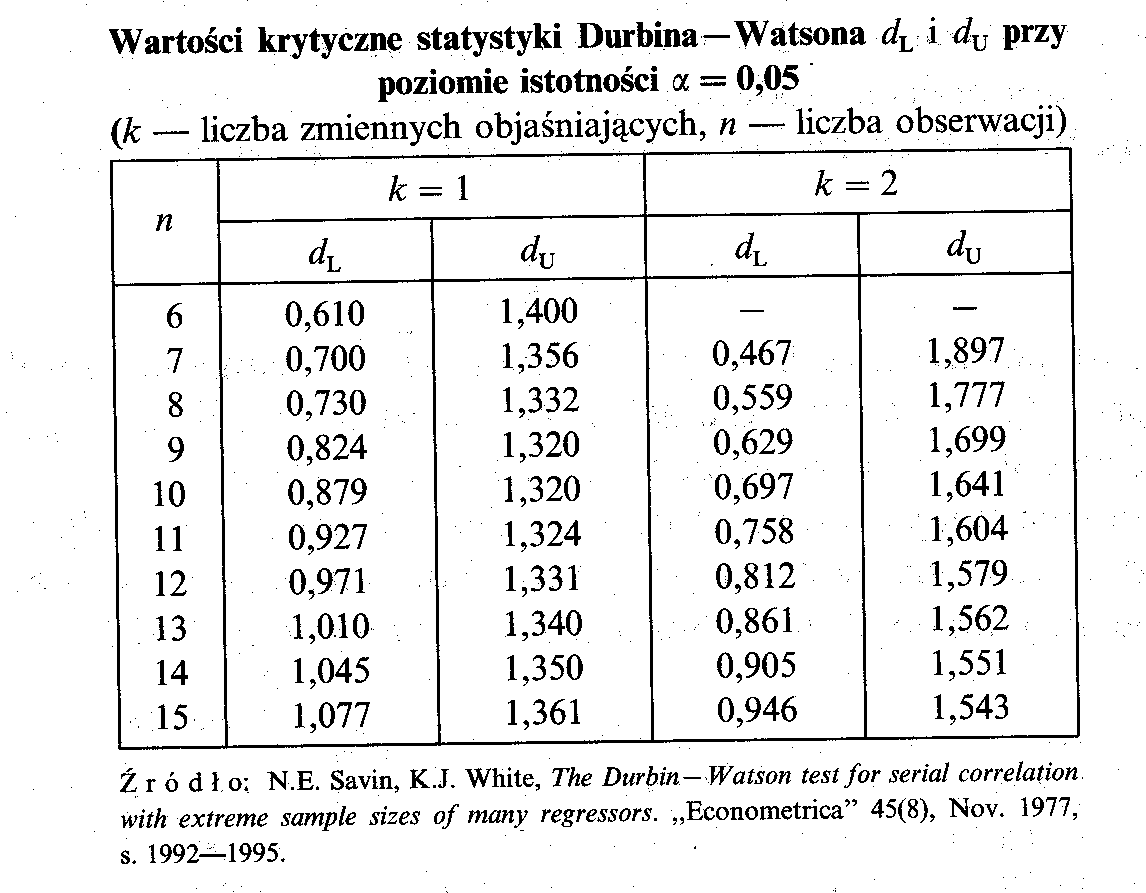
I. Dla r > 0 (0<r<1) czyli H₁: ρ > 0

1. jeżeli d ≤ d_L, to odrzucamy hipotezę zerową, zatem stwierdzamy występowanie autokorelacji;

2. jeżeli d ≥ dU, to przyjmujemy ρ = 0, zatem stwierdzamy, że w badanym modelu autokorelacja nie występuje;

3. jeżeli d_L < d < d_U, to test nie daje odpowiedzi i nie możemy podjąć decyzji o przyjęciu lub odrzuceniu H₀.
   (d wpadło tu w przedział niekonkluzywności)

II. Dla r <0 (-1<r<0) czyli H₁: ρ < 0

1. jeżeli 4-d ≤ dL, to odrzucamy hipotezę zerową, zatem stwierdzamy występowanie autokorelacji;

2. jeżeli 4-d ≥ d_U, to przyjmujemy ρ = 0, zatem stwierdzamy, że w badanym modelu autokorelacja nie
   występuje;

3. jeżeli d_L < 4-d < d_U, to test nie daje odpowiedzi i nie możemy podjąć decyzji o przyjęciu lub
   odrzuceniu H₀.

Stosowanie testu Durbina-Watsona wymaga, aby:

1. W równaniu obecny był wyraz wolny.

2. Zakłócenia miały rozkład normalny.

3. W równaniu nie występowała opóźniona zmienna objaśniana w charakterze zmiennej objaśniajacej.

Jeżeli w modelu zmienna objaśniającą jest opóźniona zmienna objaśniana:

y_t = f(y_t-1,…) + ε_t to statystyka d jest obciążona, a więc nie należy jej stosować.

Stosujemy wtedy statystykę h (DurH) o postaci:

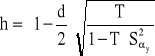
warunek stosowalności: S² >(1/T).

- to kwadrat błędu średniego dla parametru α stojącego przy opóźnionej zmiennej objaśnianej

T - liczba obserwacji

Możliwość stosowania przy różnych opóźnieniach zmiennej y.

---