TEMAT ĆWICZENIA:

Badanie drgań tłumionych wahadła Torsyjnego

1. Wstęp teoretyczny do wykonywanego zadania.

2. Tabele pomiarowe.

3. Obliczenia, wnioski i wykresy.

1. Wprowadzenie

Ruch obrotowy ciała sztywnego wokół stałej osi opisany jest równaniem:

,

gdzie I jest momentem bezwładności ciała względem tej osi,
jest jego przyspieszeniem kątowym (φ jest kątem obrotu ciała wokół własnej osi), a M jest momentem siły, względem rozważanej osi, działającym na ciało. Jeżeli moment siły M jest znaną funkcją kąta φ, prędkości kątowej
i czasu t, to powyższe równanie ruchu z warunkami początkowymi:
oraz
jednoznacznie wyznacza ruch ciała sztywnego.

Jeśli pomiędzy momentem siły M i kątem φ zachodzi zależność proporcjonalna o ujemnym współczynniku proporcjonalności, równanie ruchu ma postać:

gdzie k₁ jest dodatnią stałą, nazywaną momentem kierującym. Źródłem takiego momentu siły są siły sprężystości elementu, do którego przymocowane jest ciało. Jest to jak widać z równania ruch harmoniczny. Jeżeli oprócz momentu siły: -k₁φ na ciało działa moment siły zwrócony przeciwnie do jego prędkości kątowej
, to ruch ciała jest tłumiony. Gdy tłumienie przekroczy pewną krytyczną wartość, ruch przestaje być ruchem drgającym.

W wykonywanym ćwiczeniu występują dwa najprostsze rodzaje tłumienia:

1. tłumienie występujące przy tarciu suchym (kulombowskim) - tłumienie momentem siły M' stałym co do wartości, lecz zwróconym przeciwnie do prędkości kątowej ciała:

,
,

Równanie ruchu ma zatem postać:

,

Maksymalne wychylenia ciała z położenia równowagi maleją o stałą wartość:

na każdy okres, a więc wychylenie maksymalne maleje liniowo w zależności od czasu.

2. tłumienie wiskotyczne - tłumienie momentem siły M” proporcjonalnym do prędkości kątowej i zwróconej do niej przeciwnie:

,

Równanie ruchu jest następujące:

Jeżeli tłumienie jest na tyle małe, że
, to można sprawdzić, że rozwiązaniem równania ruchu jest:

gdzie Φ i ε są stałymi, które wyznacza się na podstawie warunków początkowych, natomiast:

,

Okres tych drgań wynosi:

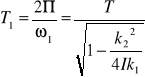
Okres ten jest dłuższy od okresu drgań niegasnących. Stosunek dwu kolejnych wychyleń, po tej samej stronie położenia równowagi:

jest stały i nosi nazwę stosunku tłumienia. Logarytm z tej wielkości jest często używaną miarą tłumienia tego typu drgań i nosi nazwę logarytmicznego dekrementu tłumienia drgań:

2. Tabele Pomiarowe

Liczba okresów	Wychylenie
1T	200
2T	190
3T	184
4T	170
5T	156
6T	146
7T	136
8T	128
9T	120
10T	113
11T	108
12T	105
13T	100

2a) Drganie bez tłumienia

Średni czas 10 okresów: 1 min 52 sek.

2b) Drgania z tłumieniem w wodzie

Liczba okresów	Wychylenie
1T	111
2T	110
3T	110
4T	109
5T	108
6T	107
7T	108
8T	107
9T	106
10T	105
11T	104
12T	104
13T	103

Średni czas 10 okresów: 1 min 51 sek.

3a) Obliczenia do zadania nr 1:

• Moment bezwładności

m = 1,000 kg

R = 0,0313 m

• Moment kierujący k₁

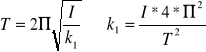
T = 1 min 52 sek =112[s]

3b) Obliczenia do zadania nr 2:

• Stosunek dwu kolejnych wychyleń, po tej samej stronie położenia równowagi:

ϕ_n, ϕ_n+1 - dwa kolejne maksymalne wychylenia, to tej samej stronie

ϕ_n = 184

ϕ_n+= 170

;

• Logarytmiczny dekrement tłumienia

;

• Współczynnik k₂

T₁ = 1 min 52 sek = 112 sek

3c) Wnioski

Amplituda drgań nie tłumionych maleje liniowo i bardzo powoli, aby takie drgania ustały musi minąć długi czas. W drugiej części ćwiczenia tłumiliśmy drgania za pomocą wody. W tym przypadku -tłumienia wiskotycznego - amplituda malała wykładniczo - bardzo szybko.

---