WYDZIAŁ ELEKTRONIKI
KATEDRA MIERNICTWA ELEKTRONICZNEGO
LABORATORIUM PODSTAW MIERNICTWA
GRUPA: 4a
Ćwiczenie nr 6	Imię i nazwisko	informa
Temat: Pomiary elementów RLC	Data wykonania ćwiczenia	1999-05-18
	Data odbioru sprawozdania	1999-05-27
	Ocena zaliczenia
	Uwagi

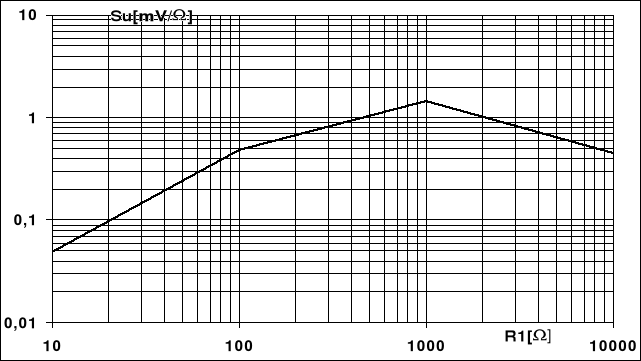
1.Zależność czułości napięciowej od rezystancji

Wykres czułości w zależności od zmian rezystora R₁.

Wykres czułości w zależności od zmian rezystora R₂.

Z powyższych wykresów oraz wyników pomiarów i obliczeń wynika że największą czułość mostka Wheatstone'a uzyskałem dla R₁ = 1000 Ω, z kolei wpływ wartości rezystancji R₂ na czułość napięciową tego mostka okazał się bardzo znikomy - maksymalną i prawie stałą czułość mostka uzyskałem dla wartości rezystancji R₂ większych od 100 Ω.

Ponieważ wartość mierzona R_x wynosiła w czasie pomiaru 1000 Ω można stwierdzić, że mostek Wheatstone'a uzyskuje optymalne warunki pomiaru (maksymalną czułość napięciową), gdy wartość rezystancji R₁ jest równa, albo przynajmniej zbliżona do wartości rezystancji mierzonej R_x, czyli gdy spełniony jest warunek R₁=R_x, a co do wartości rezystancji R₂ to nie ma ona znaczącego wpływu na warunki pracy, ale jak widać z wykresu nie powinna ona być zbyt mała.

2. Obliczanie grubości ścieżki.

Aby obliczyć wartość grubości badanej przeze mnie ścieżki obwodu drukowanego korzystam ze wzoru o następującej postaci:

gdzie: R - rezystancja badanej ścieżki obwodu drukowanego. Wynosi ona 62.6 mΩ;

σ - przewodność materiału z jakiego wykonana jest badana ścieżka. W tym przypadku wynosi 56 m/Ωmm², ponieważ ścieżka jest wykonana z miedzi;

S - pole powierzchni przekroju poprzecznego badanej ścieżki;

l - długość badanej ścieżki obwodu drukowanego. (0.05 m)

Ponieważ pole powierzchni S przekroju poprzecznego badanej ścieżki obwodu drukowanego jest opisane wzorem:

gdzie: a - poszukiwana przez grubość badanej ścieżki obwodu drukowanego;

b - szerokość badanej ścieżki. (2 mm)

więc wzór początkowy przyjmuje następującą postać:

Po przekształceniach otrzymuję wzór na grubość ścieżki obwodu drukowanego a o postaci:

W oparciu o ten wzór otrzymałem następującą wartość grubości ścieżki cynowanej:

oraz grubość ścieżki miedzianej:

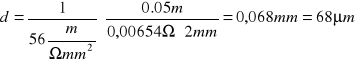
3. Obliczanie błędu pojemności

Przy uzupełnianiu tabel 6.4 i 6.5 skorzystałem ze wzoru na względny błąd pomiaru pojemności kondensatora o postaci:

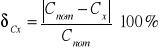
gdzie: C_nom - wartość nominalna pojemności badanego kondensatora. W tym przypadku jest wartość pojemności zmierzona w punkcie 4.3 równa 159nF

Cx - wartość zmierzona pojemności.

Przy obliczeniach skorzystaliśmy także ze wzoru na stratność kondensatora w konfiguracji:

- szeregowej - równoległej

gdzie: C_s, C_p -nominalna pojemność odpowiednio w konfiguracji szeregowej i równoległej.

R_s, R_p - rezystancja podłączona odpowiednio szeregowo i równolegle do kondensatora;

 - pulsacja sygnału pomiarowego i wynosi f (w przypadku miernika E317A f=1kHz).

Na podstawie wypełnionych tabelek 6.4 i 6.5 wykonałem na wspólnym wykresie zależność błędu pomiaru δ_Cx od współczynnika strat D_s i D_p. Wykres ten znajduje się poniżej.

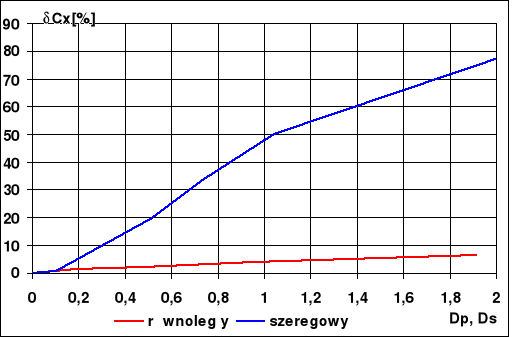
Duża różnica przebiegów charakterystyk dla konfiguracji szeregowej i równoległej, a więc i duże różnice błędów popełnianych przez miernik, wynikają z tego, że miernik E317A z zasady działania mierzy pojemności kondensatorów w konfiguracji równoległej. Taki stan rzeczy pociąga za sobą bardzo duży błąd pomiaru pojemności kondensatorów w konfiguracji szeregowej za pomocą miernika E317A, właśnie taką sytuację obrazuje powyższy wykres.

4. Omówienie pomiaru małych pojemności

Na podstawie pomiarów w punkcie 4.5. wnioskuję, że przy pomiarach bardzo małych pojemności z użyciem zwykłych przewodów zbliżanie przewodów do siebie powoduje wzrost wartości mierzonej przez miernik (C_max=171pF), zaś ich oddalanie powoduje zmniejszanie zmierzonej przez miernik wartości pojemności (C_min=106pF). Taki efekt jest wywołany tym, że miernik mierzy sumę pojemności kondensatora i pojemności przewodów łączących miernik z tym kondensatorem. Wiadomo jednocześnie, że pojemność kondensatora jest odwrotnie proporcjonalna do odległości okładek. Właśnie tę właściwość obserwowałem przy rozsuwaniu i przysuwaniu przewodów. Rozsunięcie przewodów powoduje zmniejszenie pojemności przewodów, a więc zmniejsza też błąd pomiaru pojemności, z kolei zbliżanie przewodów powoduje zwiększanie pojemności przewodów, a co za tym idzie błąd pomiaru pojemności. Jak widać w tym ćwiczeniu wkład pojemności przewodów doprowadza do błędu pomiaru pojemności 61%.

Aby zlikwidować ten niekorzystny efekt stosujemy specjalny przewód z ekranem do pomiaru pojemności. Jednak, gdy ekranu nie uziemi się ekranu to można zaobserwować podobnie duże przekłamania pomiaru pojemności (C₁=163pF) co w poprzednim przypadku, a co za tym idzie błąd pomiaru pojemności kondensatora podobnego rzędu (w tym przypadku jest to 53,7%). To zjawisko jest związane z tym, że przy nie uziemionym ekranie do pojemności mierzonego kondensatora dodaje się pojemność ekranu przewodu. Jednak gdy uziemimy ekran przewodu wtedy znika wpływ pojemności przewodu na pojemność mierzoną (C₂ = 106pF), na pojemność mierzoną nie ma wpływu wtedy też ułożenie przewodu itp.

5. Obliczanie modułu i kąta fazowego zmierzonej zmierzonej impedancji

Ogólny wzór opisujący impedancję szeregowego połączenia cewki indukcyjnej L_x i rezystancji R_x ma następującą postać:

Wtedy wzory na moduł impedancji |Z_x| i kąt przesunięcia fazowego _x wnoszonego przez element mają następującą postać:

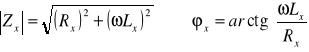
W oparciu o te wzory otrzymałem następujące wartości modułu impedancji |Z_x| i kąta fazowego _x:

Warto przypomnieć, że teoretycznie kąt powinien wynosić 90^o, więc badana cewka posiadała zbliżona do cewki idealnej.

6. Błedy pomiaru pojemności

Przy uzupełnianiu tabeli 6.6 skorzystałem ze wzoru na błąd względny pomiaru pojemności δ_Cx o postaci:

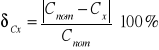
gdzie: C_nom - wartość nominalna pojemności badanego kondensatora. W tym przypadku jest wartość pojemności zmierzona na początku ćwiczenia 4.7 równa 162.44 nF.

Cx - wartość zmierzona pojemności.

Na podstawie uzyskanych w tabeli 6.6 wartości wykreśliłem zależność względnego błędu pomiaru pojemności δ_Cx w funkcji rezystancji bocznikującej R_d. Wykres ten znajduje się poniżej.

Wykres zależności względnego błędu pomiaru pojemności δ_Cx w funkcji rezystancji R_d

Jak widać na podstawie wyników uzyskanych w ćwiczeniu 4.7 i 4.4 jeżeli mierzymy pojemności o dużym współczynniku strat D lub zbocznikowanych rezystancją R, niewielki błąd pomiarowy zapewni nam miernik E317A, który z zasady działania jest przystosowany do pomiaru takich pojemności. Z kolei miernik M-4650CR może nam jedynie służyć do otrzymania pewnej orientacyjnej wielkości mierzonej pojemności (o dużym współczynniku strat), gdyż błędy jakie popełnia ten miernik są znacznie większe niż w przypadku miernika E317A.

---