Wydział: FTiMK	Imię i Nazwisko: Marcin Wiśniowski	Nr. Zespołu 5	Ocena Ostateczna
Grupa: Druga	Tytuł ćwiczenia: Dyfrakcja i interferencja światła lasera na szczelinach	Nr. Ćwiczenia 27	Data Wykonania: 22.11.2002

1. Wprowadzenie

W zjawiskach optycznych decydującą rolę odgrywa wektor pola elektrycznego E (zwany wektorem świetlnym), który dla monochromatycznej fali płaskiej dany jest wzorem:

k - wektor falowy o kierunku propagacji fali = 2π/λ

r - wektor położenia

Z falową naturą światła związane są zjawiska dyfrakcji i interferencji. Jeśli za wąską szczeliną o szerokości a, na którą pada świetlna o długości λ umieścimy ekran w odległości L >> a, to będziemy na nim obserwować układ jasnych i ciemnych prążków o zmieniającym się natężeniu. Powstanie takiego obrazu dyfrakcyjnego możemy wytłumaczyć na podstawie zasady Huyghensa i zjawiska interferencji. Położenia ciemnych prążków czyli minimów natężenia światła dane są warunkiem:

a - szerokość szczeliny

Dla bardzo wąskich szczelin, dla których spełniony jest warunek λ > a nie istnieje taki kąt α₁ , dla którego mogłoby nastąpić wygaszenie w wyniku zjawiska dyfrakcji i fala ugięta na szczelinie oświetla centralną część ekranu w sposób równomierny. Zjawisko dyfrakcji można łatwo zaobserwować w przypadku użycia w doświadczeniu wiązki światła laserowego.

Interferencja fal polega na nakładaniu się dwu lub więcej fal harmonicznych o tej samej długości prowadzącym do powstania ustalonego w czasie przestrzennego rozkładu obszarów wzmocnienia i osłabienia fali wypadkowej. Zjawisko to możemy obserwować, gdy światło pada na dwie wąskie szczeliny i po przejściu przez nie daje obraz interferencyjny składający się z na przemian jasnych i ciemnych prążków o prawie jednakowym natężeniu. Warunek wzmocnienia (prążka jasnego):

σ - różnica dróg optycznych,

przy założeniu że odległość szczelin od ekranu L >> d (odległość między szczelinami), różnica dróg optycznych σ wyraża się wzorem:

Jasne prążki interferencyjne występują gdy:

W przypadku realnych szczelin, których szerokości są większe lub porównywalne z długością fali świetlnej a ≈ λ lub λ < a zjawisko dyfrakcji i interferencji występują razem.

2. Tabele Pomiarowe

Tabela 1.

L = 95,2 cm λ = 670 nm
Nr pomiaru	y [mm]	U [V]	Nr pomiaru	y [mm]	U [V]
1	-25	-0,05	27	1	37,22
2	-24	-0,04	28	2	39,64
3	-23	-0,04	29	3	31,79
4	-22	-0,04	30	4	20,37
5	-21	-0,03	31	5	6,72
6	-20	-0,03	32	6	1,46
7	-19	-0,02	33	7	1,23
8	-18	-0,01	34	8	1,47
9	-17	-0,03	35	9	1,20
10	-16	-0,03	36	10	0,42
11	-15	0,01	37	11	0,25
12	-14	0,04	38	12	0,35
13	-13	0,02	39	13	0,28
14	-12	-0,01	40	14	0,17
15	-11	0,06	41	15	0,08
16	-10	0,20	42	16	0,10
17	-9	0,21	43	17	0,13
18	-8	0,08	44	18	0,07
19	-7	0,20	45	19	0,03
20	-6	0,54	46	20	0,02
21	-5	0,99	47	21	0,03
22	-4	0,58	48	22	0,01
23	-3	0,73	49	23	-0,01
24	-2	3,68	50	24	-0,02
25	-1	13,47	51	25	-0,01
26	0	25,65

Tabela 2.

Nr. Minimum N	Położenie yn [mm]	an [μm]
1	-4	106,5
2	-8	128,3
3	-12	138,2
4	-16	144,3

Ćwiczenie 1 - Dyfrakcja promienia lasera na szczelinie

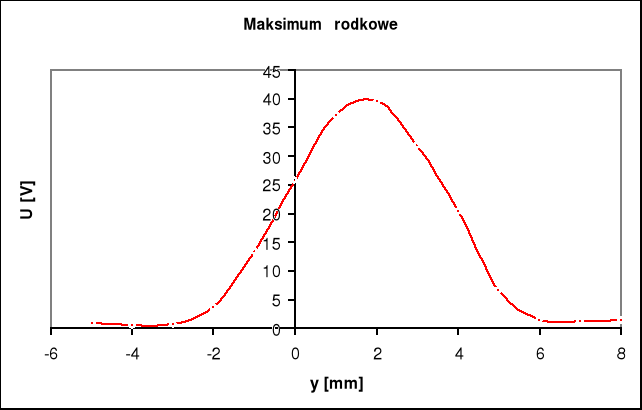
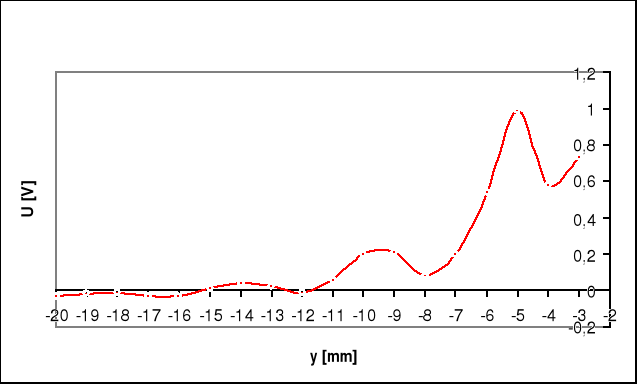
Obliczam szerokość szczeliny za pomocą wzoru:

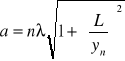
Uwzględniam przy tym przesuniecie głównego maksima o 2 mm względem środka osi symetrii, zatem wzór wyglądać będzie następująco

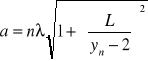
Szerokość szczeliny przyjmuje jako średnią arytmetyczną otrzymanych wyników:

Obliczamy maksymalną niepewność Δa_n dla jednego pomiaru a₂, a następnie niepewność procentową:

Otrzymana wartość szerokości szczeliny a spełnia nierówności L >> a > λ.

Ćwiczenie 2 - Siatka dyfrakcyjna

Pomiar 1		Pomiar 2
nr	yn [mm]	nr	yn [mm]
0	1	0	1
1	9	1	-8
2	18	2	-16

Obrazem na ekranie, który uzyskaliśmy prze przepuszczenie promienia lasera przez siatkę dyfrakcyjną jest szereg prążków dyfrakcyjnych.

Odległość L (siatki od fotoogniwa) została zachowana z poprzedniego ćwiczenia

L = 95,2 [cm]

Stałą siatki liczę ze wzoru

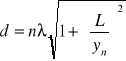
Wyznaczamy stałą siatki dyfrakcyjnej d jako średnią arytmetyczną z przeprowadzonych pomiarów.

Ilość linii przypadających na 1 cm siatki to: 1328.

Obliczamy maksymalną niepewność Δa_n dla jednego pomiaru a₂, a następnie niepewność procentową:

Ostatecznie:

d = 75,3 ± 4,5μm

Ćwiczenie 3 - Obserwacja płaszczyzny polaryzacji światła laserowego

	Kąt	U [V]
Zaciemnienie	330°	2,68·10^-3
Rozjaśnienie	58°	345,8·10^-3

Obliczam stopień polaryzacji wiązki światła ze wzoru:

Zatem:

Możliwe błędy przy tym pomiarze wynikają z błędu pomiarowego kąta równego 0,5° oraz niedoskonałości urządzenia pomiarowego

1

---