Wydział: FTiMK |
Imię i Nazwisko: Marcin Wiśniowski |
Nr. Zespołu 5 |
Ocena Ostateczna |
Grupa: Druga |
Tytuł ćwiczenia: Polaryzacja liniowa i kołowa światła |
Nr. Ćwiczenia 26 |
Data Wykonania: 15.11.2002 |
Wprowadzenie
Światło jest falą elektromagnetyczną poprzeczną. Wektory natężenia pól: elektrycznego E i magnetycznego H drgają w kierunkach prostopadłych do siebie i do kierunku rozchodzenia się fali. Światło spolaryzowane liniowo to takie, w którym wektor świetlny drga w jednej płaszczyźnie. Dla fali monochromatycznej o długości λ spolaryzowanej w płaszczyźnie y, z równanie fali jest dane wzorem:
![]()
E0z - amplituda drgań wektora E
T - okres drgań
t - czas
Polaryzację liniową można uzyskać przez odbicie od dielektryka (prawo Brestera) lub wykorzystując zjawisko dwójłomności kryształów anizotropowych. Polaroid jest to cienka warstwa zorientowanych zgodnie kryształów herapatytu (jodosiarczanu chininy) umieszczona między dwiema przeźroczystymi foliami. Promień światła padający na polaroid dzieli się na dwa promienie zwyczajny i nadzwyczajny, oba spolaryzowane liniowo w płaszczyznach do siebie prostopadłych (zjawisko dwójłomności). Jeden z nich jest niemal całkowicie pochłonięty (zjawisko to nazywa się dichroizmem).
Światłem spolaryzowanym kołowo nazywamy światło, w którym koniec wektora świetlnego obiega ruchem jednostajnym okrąg. Można je uważać za wynik superpozycji dwóch drgań spolaryzowanych liniowo wzdłuż dwóch osi do siebie prostopadłych, o tych samych amplitudach i częstościach, ale różniących się w fazie o ½ Π(2n+1). Światło spolaryzowane kołowo uzyskujemy przez przepuszczenie wiązki światła spolaryzowanego liniowo przez odpowiednio ustawioną ćwierćfalówkę.
Ciałami optycznie czynnymi nazywamy ciała skręcające płaszczyznę polaryzacji światła spolaryzowanego liniowo. Kąt α skręcenia płaszczyzny polaryzacji jest wprost proporcjonalny do długości l warstwy skręcającej i do stężenia c roztworu (dla roztworów):
![]()
Dwójłomnością wymuszoną nazywamy dwójłomność pojawiającą się w ciałach izotropowych mechanicznie i optycznie na skutek wzbudzonego w nich stanu naprężenia lub umieszczenia ich w silnych polach elektrycznych, lub magnetycznych. Płytka materiału izotropowego poddana ściskaniu w jednym kierunku zachowuje się jak kryształ jednoosiowy o osi optycznej zgodnej z kierunkiem sił ściskających.
Tabele Pomiarowe
Lp. |
φ |
x |
|
1 |
90° |
x0= 29 |
0 |
2 |
80° |
46 |
4,12 |
3 |
70° |
66 |
6,08 |
4 |
60° |
75 |
6,78 |
5 |
50° |
79 |
7,07 |
6 |
40° |
81 |
7,21 |
7 |
30° |
82 |
7,28 |
8 |
20° |
83 |
7,34 |
9 |
10° |
83,5 |
7,38 |
10 |
0° |
84 |
7,41 |
Lp |
ϕ1 |
ϕ2 |
α |
1 |
355 |
9 |
14 |
2 |
354 |
10 |
16 |
3 |
359 |
15 |
16 |
4 |
0 |
16 |
16 |
5 |
359 |
15 |
16 |
6 |
359 |
14 |
15 |
7 |
358 |
15 |
17 |
8 |
358 |
15 |
17 |
9 |
359 |
15 |
16 |
10 |
359 |
15 |
16 |
l = 10,05 [cm]
c = 0,20 [g/cm3]
Ćwiczenie 1 - Sprawdzenia Prawa Malusa:
Zamieszczony wykres przedstawia wyniki pomiarów prądu w zależności od wartości konta między polaryzatorem a analizatorem. Wykres wykonany jest w układzie współrzędnych biegunowych, w którym współrzędna transwersalna jest równa kontowi między polaryzatorem a analizatorem, a współrzędna radialna wynosi ![]()
. Wykres ten przedstawia pół okrąg zbudowany na ![]()
jako średnicy.
Z trójkąta OAA' otrzymujemy:
![]()
Ponieważ (x - xo) jest proporcjonalne do I, więc
I = Iocos2ϕ
(Prawo Malusa)
Niestety nasz wykres odbiega nieco od pierwotnej koncepcji wynikać to może z niedoskonałości przyrządów oraz oka ludzkiego, jak również z przypadków losowych takich jak zmiana natężenia światłą lampy emitującej promieni świetlne użytej w tym ćwiczeniu.
Ćwiczenie 2 - Wyznaczenie zdolności skręcającej roztworu sacharozy:
Z otrzymanych wyników wyznaczam wartości średnie kątów ϕ1 i ϕ2 jednocześnie przyjmując niepewność pomiaru równą 0,5°
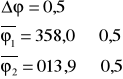
Wyliczam kąt skręcenia αo roztworu sacharozy:
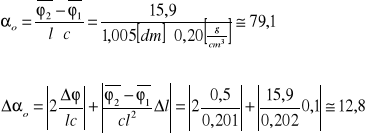
Ostatecznie kąt skręcenia wynosi:
![]()
Spełnia ona kryterium zgodności, bowiem wartość tablicowa tej wielkości wynosi α0 = 66,46 i mieści się w przedziale określonym przez niepewność pomiarową Δα0.
4
Wyszukiwarka
Podobne podstrony:
ćw 26 - sprawko moje, Szkoła, Semestr 4, Podstawy elektroniki, Bart, Podstawy Elektroniki LAB, Podst
Podstawy zarządzania cw 6 26 01 2008
Cw 26 Elementy kontrolne
obliczenia do ćw 26
jurek 26, Fizyka, ćw 26
Fizyka ćw. 26
cw 26
ćw.26, Fizyka, Skrypt do Laborek
cw 26
ćw.27, cw27, R1=
ćw 26 - sprawko moje kopia, Szkoła, Semestr 4, Podstawy elektroniki, Bart, Podstawy Elektroniki LAB,
Odbiornik nasłuchowy SSB CW 26 30MHz
Cw 4 26 10 12
Ćw 26 szablon
Finanse przedsiębiorstw ćw. 26.10.2008, Zarządzanie i marketing
ćw 26 04 20 05 (treść zadań)
ćw.22, cw22, R1=
Sprawozdanie ćw. 26
więcej podobnych podstron