Zestaw 2

1. Zmienna losowa X ma rozkład N(0,1).

1. Obliczyć P(X>2,25), P(X<-2,25), P(|X|>1,5), P(|X|<1,15).

2. Obliczyć
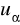
   : P(X <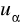
   ) = 0,9; P(X <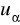
   ) = 0,95; P(X <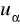
   ) = 0,99; P(|X| <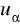
   ) = 0,9; P(|X| <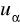
   ) = 0,95; P(|X| <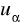
   ) = 0,99

2. Dochody z reklamy pewnego tygodnika mają rozkład normalny z wartością oczekiwaną 8 tyś. zł i odchyleniem standardowym. 500 zł. Jakie jest prawdopodobieństwo, że dochody z reklamy w pewnym tygodniu będą

a) większe niż 8,5 tyś zł,

b) większe niż 8,25 tyś zł i mniejsze niż 8,75 tyś zł,

c) nie przekroczą 8,5 tyś zł

3. Czas spożywania obiadu w stołówce przez studentów jest zmienną losową o rozkładzie normalnym
   N(30 min, 10 min). Obliczyć:

a) jaka część studentów spożywa obiad przeciętnie krócej niż 15 min?

b) jaki jest czas spożywania obiadu 10% najkrócej spożywających obiad studentów?

4. Zmienna losowa X ma rozkład normalny N(5,3). Obliczyć:

a) P(X>6,5)

b) s jeżeli P(X>s) = 0,08

5. Kolejka podmiejska zabiera 121 pasażerów. Przyjmując, że średnia waga pasażerów wynosi 70kg z odchyleniem standardowym 5kg, obliczyć prawdopodobieństwo zdarzenia, ze waga netto kolejki przekroczy 8,5t.

6. Pobrano partię jogurtów składającą się z 225 sztuk. Waga każdego jogurtu wynosi 150g z odchyleniem 12g. Obliczyć prawdopodobieństwo, że średnia waga jest mniejsza niż 151g.

7. Pewien niewielki zakład transportowy jest w stanie wynająć jednego dnia dwa samochody. Przypuśćmy, że dzienna liczba zgłoszeń klientów jest zmienną losową o rozkładzie Poissona z parametrem lambda = 1,6.

1. Jaką część w działalności firmy stanowią dni kiedy nikt nie zgłaszał się po samochód ?

2. Jaką dni kiedy liczba klientów przekroczyła możliwości firmy?

3. Jaka jest oczekiwana dzienna liczba zgłoszeń klientów?

1. W urnie znajdują się cztery kule z numerem „0” oraz jedna kula z numerem „1”. Wyciągamy jedną kulę z urny. Niech X oznacza numer widniejący na wyciągniętej kuli. Jaki rozkład charakteryzuje zmienna losową X? Zapisać i zaprezentować graficznie funkcję rozkładu prawdopodobieństwa oraz dystrybuantę.

2. Z bieżącej produkcji samochodów pewnej marki wylosowano 4 auta. Niech X oznacza liczbę aut z usterką układu hamulcowego. Wiadomo, że prawdopodobieństwo wykrycia usterki układu w pojedynczym samochodzie wynosi 0,2. Jaki rozkład charakteryzuje zmienna losową X? Zapisać i zaprezentować graficznie funkcję rozkładu prawdopodobieństwa oraz dystrybuantę.

3. W pewnym przedsiębiorstwie zaobserwowano, ze w ciągu miesiąca zdarzają się średnio 2 wypadki i że rozkład liczby wypadków może być opisany za pomocą rozkładu Poissona. Obliczyć P(X<3) oraz P(X>3).

---