PRACOWNIA FIZYCZNA AKADEMII PODLASKIEJ |
|||
W SIEDLCACH |
|||
|
Grupa |
||
Imię i Nazwisko, kierunek studiów |
|
||
Nr ćwiczenia |
Data wykonania |
Ocena zaliczenia |
Podpis |
Temat: Pomiar natężenia pola grawitacyjnego przy pomocy modelu wahadła matematycznego.
1. Schemat budowy wahadła matematycznego.
D - średnica kulki
l' - długość nici
l - długość wahadła
Φ0 - kąt wychylenia
2. Przyrządy pomiarowe.
miarka milimetrowa
wahadło matematyczne
katetometr (0,001 m)
suwmiarka
3. Tabela pomiarów:
|
|
D |
l' |
l |
t20 |
T |
Tśr |
l/T2 |
Φ0 |
g |
gśr |
Δg |
Δgśr |
|
|
m |
m |
m |
s |
s |
s |
m/s2 |
rad |
m/s2 |
m/s2 |
m/s2 |
m/s2 |
I seria pomiarów |
1 |
0,03868 |
0,35 |
0,36934 |
23,7 |
1,185 |
1,185 |
0,31168 |
0,087 |
12,292166 |
12,35329 |
0,07466 |
0,07563 |
|
2 |
|
|
|
23,4 |
1,17 |
|
|
|
|
|
|
|
|
3 |
|
|
|
24 |
1,2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
23,6 |
1,18 |
1,17333 |
0,31478 |
0,174 |
12,414419 |
|
0,0766 |
|
|
5 |
|
|
|
23 |
1,15 |
|
|
|
|
|
|
|
|
6 |
|
|
|
23,8 |
1,19 |
|
|
|
|
|
|
|
II seria pomiarów |
1 |
0,03868 |
0,7005 |
0,71984 |
33,06 |
1,652 |
1,65233 |
0,26366 |
0,087 |
10,39832 |
10,30525 |
0,04735 |
0,04678 |
|
2 |
|
|
|
33,08 |
1,654 |
|
|
|
|
|
|
|
|
3 |
|
|
|
33,04 |
1,651 |
|
|
|
|
|
|
|
|
4 |
|
|
|
33,02 |
1,651 |
1,66733 |
0,25894 |
0,174 |
10,21218 |
|
0,04622 |
|
|
5 |
|
|
|
33,02 |
1,651 |
|
|
|
|
|
|
|
|
6 |
|
|
|
34 |
1,7 |
|
|
|
|
|
|
|
D - średnica kulki
l' - długość nici
l - długość wahadła
t20 - czas trwania 20 okresów
T - okres
Φ0 - kąt wychylenia
g - natężenie pola grawitacyjnego
Celem ćwiczenia jest wykonanie pomiaru natężenia pola grawitacyjnego przy pomocy
pola grawitacyjnego przy pomocy wahadła matematycznego.
I seria pomiarów.
Obliczamy długość wahadła (l) korzystając ze wzoru:
l = ½ D +l'
l = ½ ּ 0,03868 m + 0,35 m = 0,36934 m
Wykonujemy obliczenia dla poszczególnych kątów Φ0 . Wyliczmy okres T, okres średni Tśr oraz l/T2
Φ0 = 0,087 rad
T1 = 23,7 / 20 = 1,185 s
T2 = 23,4 / 20 = 1,17 s
T3 = 24 / 20 = 1,2 s
Tśr123 = (T1 + T2 + T3 ) / 3 =1,185 s
l / T2śr123 = 0,36934 / 1,185 = 0,31168 m/s
Φ0 = 0,174 rad
T4 = 23,6 / 20 = 1,18 s
T5 = 23 / 20 = 1,15 s
T6 = 23,8 / 20 = 1,19 s
Tśr456 = (T4 + T5 + T6) / 3 = 1,17333 s
l / T2śr456 = 0,36934 / 1,17333 = 0,31478 m/s
Obliczamy natężenie pola grawitacyjnego ze wzoru
g = 4ּπ2ּl / T2
g123 = 4ּπ2ּ0,31168 = 12,292160 m/s2
g456 = 4ּπ2ּ0,31478 = 12,414419 m/s2
Obliczamy średnie natężenie pola grawitacyjnego jako średnią arytmetyczną.
gśr = ( g123 + g456 ) / 2 = 12,35329 m/s2
Przechodzimy do obliczania błędu metodą różniczki zupełnej:
![]()
Przyjmujemy:
ΔD = 0,0001 m
Δl' = 0,001 m
Δl = ΔD + Δl' = 0,0001 + 0,001 = 0,0011 m
ΔT = 0,01 s
dla Φ0 = 0,087 rad
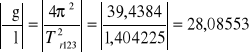
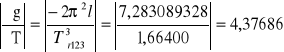
dla Φ0 = 0,0174 rad
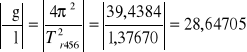
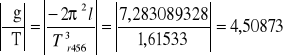
Zatem
Δg123 = 28,08553ּ0,0011 + 4,37686ּ0,01 = 0,03089 + 0,04377 = 0,07466 m/s2
Δg456 = 28,64705ּ0,0011 + 4,50873ּ0,01 = 0,0766 m/s2
Obliczamy Δgśr jako średnią arytmetyczną.
Δgśr = 0,07563 m/s2
Błąd względny dla pierwszej serii pomiarów wynosi:
g = gśr ± Δgśr
g = 12,35329 m/s2 ± 0,07563 m/s2
II seria pomiarów.
Obliczamy l korzystając ze wzoru:
l = ½ D +l'
l = ½ ּ 0,03868 m + 0,7005 m = 0,71984 m
Wykonujemy obliczenia dla poszczególnych kątów Φ0.
Φ0 = 0,087 rad
T1 = 33,06 / 20 = 1,652 s
T2 = 33,08 / 20 = 1,654 s
T3 = 33,04 / 20 = 1,652 s
Tśr123 = (T1 + T2 + T3 ) / 3 =1,65233 s
l / T2śr123 = 0,71984 / 2,73019 = 0,26366 m/s
Φ0 = 0,174 rad
T4 = 33,02 / 20 = 1,651 s
T5 = 33,02 / 20 = 1,651 s
T6 = 34 / 20 = 1,7 s
Tśr456 = (T4 + T5 + T6) / 3 = 1,66733 s
l / T2śr456 = 0,71984 / 2,77999 = 0,25894 m/s
Obliczamy natężenie pola grawitacyjnego ze wzoru
g = 4ּπ2ּl / T2
g123 = 4ּπ2ּ0,26366 = 10,39832 m/s2
g456 = 4ּπ2ּ0,25894 = 10,21218 m/s2
Obliczamy średnie natężenie pola grawitacyjnego jako średnią arytmetyczną.
gśr = ( g123 + g456 ) / 2 = 10,30525 m/s2
Przechodzimy do obliczania błędu metodą różniczki zupełnej:
![]()
Przyjmujemy:
Δl = 0,001 m
ΔT = 0,01 s
Φ0 = 0,087 rad
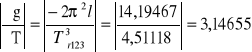
Φ0 = 0,174 rad
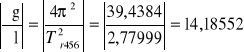
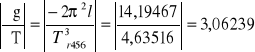
Zatem
Δg123 = 14,44529ּ0,0011 + 3,14655ּ0,01 = 0,01589 + 0,03146 = 0,04735 m/s2
Δg456 = 14,18652ּ0,0011 + 3,06239ּ0,01 = 0,04622 m/s2
Obliczamy Δgśr jako średnią arytmetyczną.
Δgśr = 0,04678 m/s2
Błąd względny dla pierwszej serii pomiarów wynosi:
g = gśr ± Δgśr
g = 10,30525 m/s2 ± 0,04678 m/s2
WNIOSKI
Celem doświadczenia było wykonanie pomiaru natężenia pola grawitacyjnego przy pomocy modelu wahadła matematycznego. Pomiary wykonaliśmy dla kątów 0,087 rad oraz 0,174 rad i dla długości wahadła 0,36934 m oraz 0,71984 m.
Błąd, który otrzymaliśmy wynika z niedoskonałości przyrządów pomiarowych oraz z niedoskonałości odczytów.
Wartości natężenia grawitacyjnego, które otrzymaliśmy na podstawie obliczeń to
g = 12,35329 m/s2 ± 0,07563 m/s2 dla wahadła o długości 0,36934 m oraz
g = 10,30525 m/s2 ± 0,04678 m/s2 dla wahadła o długości 0,71984 m.
Są one zbliżone do wartości zawartych w tablicach matematyczno-fizycznych.
![]()
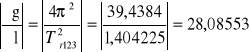
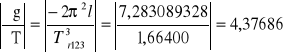
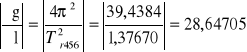
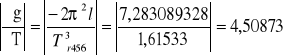
![]()
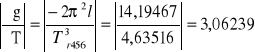
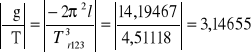

Wyszukiwarka
Podobne podstrony:
412
412, 412
412 problem reprezentacjihj
412
!412 Obwod Analiza ObwodRid 507 Nieznany (2)
412
412 Blachownica Stalowa
412 GARANT
aps 412 io pl 0814
412
412
412
Doświadczenie 412, MIBM WIP PW, fizyka 2, laborki fiza(2), 25-Interferencja światła, pierścienie New
więcej podobnych podstron