Laboratorium metrologii |
|||
Leszek Kierzek Tomasz Bartkowski
|
Temat:
Obliczanie błędów pomiarów pośrednich. |
Nr ćw. 1 |
|
WBMiZ MiBM semestr VII |
Prowadzący: mgr inż. M. Grzelka |
Data: 29.10.2003 |
|
1. Cel ćwiczenia
Celem ćwiczenia było zapoznanie się z metodami pomiarów pośrednich oraz ze sposobami obliczania ich błędów.
2. Pomiary
3.Obliczenia
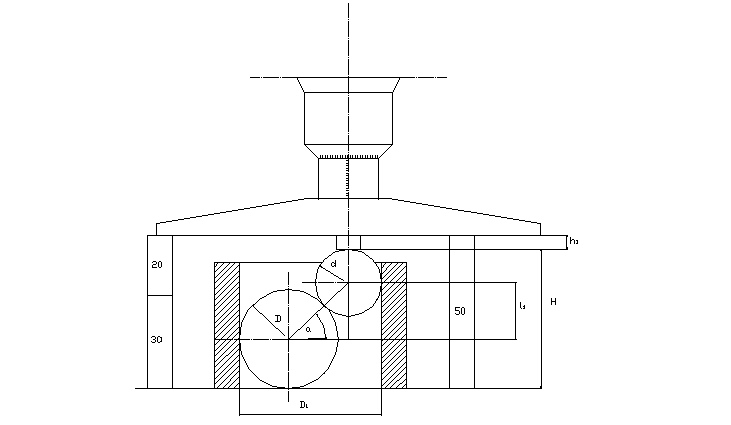
3.1
D1=∅34,00 H=50
D=∅30,13
d=∅15,88
h1=6,77
D1=(D+d)/2(1+cosα)
sinα=2(H-h1)(D+d)-1
ΔD1=±[|∂D1/∂D||ΔD|+|∂D1/∂d||Δd|+|∂D1/∂α||Δα|]
gdzie: ΔD=ΔW1+ΔR1 ; Δd=ΔW2+ΔR1
Δα=1/cosαΔy
ponieważ: y= 2h/(D+d)-1
to: Δy=[|2/D+d||ΔDh+|-2h/(D+d)2|ΔD|+|-2h/(D+d)2||Δd|]
ostatecznie:
ΔD1=±{[1+cosα+tg(sinα+1)](ΔW+ΔR)+tgα( TL+ΔWh+ΔRh)}
Dla stosu płytek wzorcowych 50mm klasy 1 wartość 0,5 TL= ±0,0005mm
ΔH=2*0,5 TL= ±0,001mm
ΔW=±0.004 ; ΔR=±0,001 a więc Δh1=±0,005mm
h=H-h1=50-6,77=43,23mm
Δh=ΔH+Δh1
Δh=0,001+0,005=±0,006mm
Ostatecznie dane z pomiarów wynoszą:
D=30,13±0,005mm; d=15,88±0,005mm; h=43,23±0,006mm
sinα=2(H-h1)(D+d)-1=0,87; α=61,6°
D1=(15,88+30,13)/2(1+cos61,6)=33,81mm
ΔD1=±{[1+cosα+tg(sinα+1)](ΔW+ΔR)+tgα( TL+ΔWh+ΔRh)}=±0,0196mm
Ostatecznie:
D1=33,81±0,0196mm
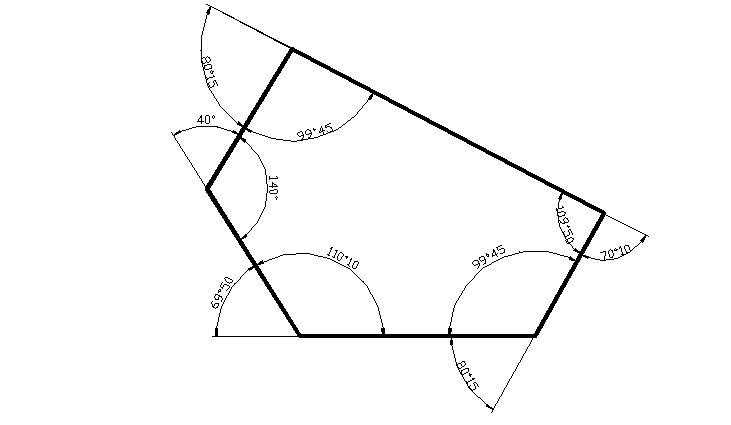
3.2
α+β+γ+δ+ϕ=99°45′+140°+110°10′+99°45′+109°50′=559°30′
Błąd odczytania: ΔR=±5′
Błąd wskazania: ΔW=±5′ (wg normy PN-82/M-53358)
Niepewność pomiaru: ΔN=±[|ΔW|+|ΔR|]=±10′
4. Wnioski:
Wyniki pomiarów mogą nieco odbiegać od obliczeń teoretycznych, mogą mieć na to wpływ: cechy konstrukcyjne narzędzia pomiarowego, zakres pomiarowy, klasa dokładności, wielkość działki elementarnej, cechy indywidualne mierzącego i inne warunki pomiarowe, jak oświetlenie itp. W pomiarach bezpośrednich niepewność pomiaru jest związana z błędem wskazania i błędem odczytu.
W przypadku pomiarów pośrednich niepewność pomiaru określa się jako sumę błędów cząstkowych poszczególnych wielkości pośrednich wchodzących w zakres pomiarowy. W naszym przypadku błędami cząstkowymi są: błąd pomiaru średnicy kulek i błąd pomiaru wysokości. Wartość błędu cząstkowego zależy od dokładności pomiaru bezpośredniego wielkości pośrednich i od pochodnej cząstkowej. Natomiast niepewność pomiaru stanowi sumą wszystkich błędów cząstkowych.
.
Wyszukiwarka
Podobne podstrony:
Błędy pomiarów pośrednich, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
metrologia - błędy kształtu, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
metrologia - błędy kształtu, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
SPRAWOZDANIE NR 1, ZiIP, II Rok ZIP, Metrologia, Sprawozdanie nr 1
sprawozdanie nr 5, ZiIP, II Rok ZIP, Metrologia, Sprawozdanie nr 5
SPRAWOZDANIE NR 1, ZiIP, II Rok ZIP, Metrologia, Sprawozdanie nr 1
str tytuł-SKJ, ZiIP, II Rok ZIP, Metrologia, SKJ-Statystyczna Kontrola Jakości, Sprawozdanie
Stożki, ZiIP, II Rok ZIP, Metrologia
częstotliwość, ZiIP, II Rok ZIP, Metrologia
SKJ wnioski, ZiIP, II Rok ZIP, Metrologia, SKJ-Statystyczna Kontrola Jakości, Sprawozdanie
sprawozdanie nr 3, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdanie nr 3
Kopia LABORATORIUM-nasze, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1
LABORATORIUM, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1), Sprawozda
Pomiary błędów kształtu, ZiIP, II Rok ZIP, Metrologia
LABORATORIUM-nasze v2, ZiIP, II Rok ZIP, Metrologia, Charkterystyka statyczna przetworników (lab1),
Politechnika Poznańska, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania, Statystyczna kontrol
POPRAWIONE 01 - Pomiary współrzędnościowe, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
Pomiary stożków, ZiIP, II Rok ZIP, Metrologia
więcej podobnych podstron