IChiP - Zestaw nr ??. Funkcje wielu zmiennych. Ekstrema funkcji.
Warunek konieczny istnienia ekstremum funkcji f : Rn → R
Jeżeli f ma ekstremum lokalne w punkcie a i jest różniczkowalna w tym punkcie to ![]()
dla i = 1,...,n
Warunek dostateczny istnienia ekstremum (dla funkcji dwóch zmiennych):
Jeżeli mamy daną funkcję dwóch zmiennych (ciągłą i mającą pochodne pierwszego i drugiego rzędu ciągłe), to aby stwierdzić, czy funkcja ta ma ekstremum w punkcie a (w którym
![]()
oraz
![]()
) - należy policzyć wyznacznik W(a) = 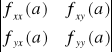
.
Jeżeli W(a) < 0 to funkcja f nie ma ekstremum w punkcie a
Jeżeli W(a) > 0 to w punkcie a jest ekstremum lokalne funkcji f, przy czym jeśli
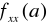
> 0, to jest to minimum, a jeśli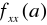
< 0, to jest to maksimum.Jeżeli W(a) = 0 to istnienie ekstremum musi być zbadane innymi metodami (być może - z definicji).
Niech f, g będą dwiema funkcjami określonymi na podzbiorach przestrzeni Rn i niech A = {x ∈ Rn: g(x) = 0}. Mówimy, że funkcja f ma w punkcie x0 ekstremum warunkowe przy warunku g(x) = 0, jeżeli f |A (f obcięta do zbioru A) ma w tym punkcie ekstremum lokalne. Aby znaleźć punkty, w których może być ekstremum warunkowe (krytyczne punkty warunkowe) stosujemy metodę mnożników Lagrange'a, tzn. określamy funkcję pomocniczą F(x) = f(x) + λg(x) (λ- parametr), i rozwiązujemy układ równań
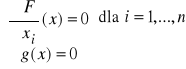
. Mamy więc (n+1) równań z (n+1) niewiadomymi (n współrzędnych punktu x oraz parametr λ). Rozwiązując ten układ otrzymujemy współrzędne krytycznych punktów warunkowych.
1) Obl. wsk. pochodne funkcji: a) f(x,y,z) = 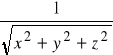
; policzyć ![]()
; b) g(x,y,z) = e xyz ; policzyć ![]()
c) ![]()
, policzyć ![]()
;d) k(x,y,z) = ![]()
, policzyć ![]()
2) Obl. poch. cząstk. funkcji a) f(x,y) = ![]()
. (Wsk.. W (0,0) policzyć z def.). b)f(x,y)= ![]()
3) Dana jest funkcja 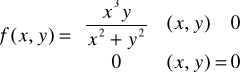
oraz F(t) = f(t2, 2t2) i G(u,v) = f(u + v, u - v)
a) Policzyć F'(0) i F'(1). b) Policzyć ![]()
c) Dodatkowo, wyk. że ![]()
.
3') Obl. poch.cząstk. do drugiego rzędu włącznie dla funkcji f(x,y)=arc tg (y/x); f(x,y)=x cos2(x+2y+z2).
3”) Znaleźć z'x, z'y a następnie z”xx, z”xy, z”yy , jeżeli z=f(u,v), gdzie u=u(x,y), v=v(x,y); zakładamy, że f,u,v mają ciągłe pochodne cząstkowe do drugiego rzędu włącznie.
4) Znaleźć ekstrema funkcji dwóch zmiennych, określonych wzorem:
a) f(x,y) = x2 + xy + y2 -2x - y b) f(x,y) = ex-y (x2 - 2y2) c) f(x,y) = sin x + cos y + cos (x-y) 0<x,y<π/2
d) f(x,y) = x2 + x2y + y2 e) f(x,y) = x2 - 6xy + y3 f) f(x,y) = x3 + y2 - 6xy - 48x
5) Znaleźć najmniejszą i największą wartość funkcji
a) f(x,y) = x3 + y2 - 3x - 2y - 1 na zbiorze D = {(x,y): x ≥0, y ≥ 0, x + y ≤ 3};
b) f(x,y,z) = ![]()
na zbiorze V = {(x,y,z): x2 + y2 + z2 ≤ 1, z ≥ 0};
c) f(x,y) = x2+y2 + x+y + xy na obszarze D = {(x,y): x≥0,y≤0,x-y≤3}.
6) Znaleźć krytyczne punkty warunkowe dla funkcji: a) f(x,y) = xy2 przy warunku x + y = 1; b) f(x,y,z) = xyz (x>0, y>0, z >0) przy warunku x2+y2+z2=3 ; c) f(x,y,z) =x+y+2z przy warunku x2+y2+z2=1;
d) f(x,y) = cos2x+cos2 y przy warunku x - y =π/4. e) f(x,y,z)=x3y-8y+z przy warunku g(x)=z - 6x2 = 0.
7) Znaleźć największą możliwą objętość prostopadłościanu o polu powierzchni całkowitej równym 6a2.
Wyszukiwarka
Podobne podstrony:
12 Twierdzenie Taylora dla funkcji wielu zmiennych (2)
C 04,5 Rachunek różniczkowy funkcji wielu zmiennych
funkcje wielu zmiennych UWM id Nieznany
10 Funkcje wielu zmiennych
Matematyka III (Ćw) Lista 06 Ekstrema lokalne i globalne funkcji wielu zmiennych Zadania
11 RACHUNEK RÓŻNICZKOWY FUNKCJI WIELU ZMIENNYCH
ek mat ii optymalizacja funkcji wielu zmiennych
140 Funkcje wielu zmiennych
04 Rozdział 02 Różniczkowanie funkcji wielu zmiennych
7 Funkcje wielu zmiennych
wykład 3 funkcje wielu zmiennych
11 3 Funkcje wielu zmiennych
11 4 Funkcje wielu zmiennych
12 wyklad funkcje dwu zmiennych
15 Funkcje wielu zmiennychid 16138
funkcje wielu zmiennych zadania od Misiaka id 182151
Funkcje wielu zmiennych 3
Matematyka III (Ćw) - Lista 05 - Rachunek rózniczkowy funkcji wielu zmiennych, Odpowiedzi
więcej podobnych podstron