TEMAT : SPRAWDZENIE PRAWA HOOKE'A I WYZNACZANIE MODUŁU YOUNGA

1. Cel ćwiczenia:

Celem ćwiczenia jest sprawdzenie prawa Hooke'a oraz wyznaczenie modułu Younga przez pomiar wydłużenia drutu zawieszonego pionowo i obciążonego obciążnikami.

2. Wstęp teoretyczny.

Zajmując się analizą ruchu lub stanu równowagi ciała posługujemy się modelami matematycznymi, które stanowią dopuszczalne przybliżenie ciał rzeczywistych. Za przykład mogą tutaj posłużyć pojęcia punktu materialnego (gdyż każde ciało ma różną od zera objętość) oraz ciała doskonale sztywnego (gdyż każde ciało, nawet najtwardsze, jak np.diament, ulega odkształceniom zmieniającym jego objętość lub kształt. Odkształcenia te mogą być niewielkie (ciała stałe) lub znaczne (ciecze,a szczególnie gazy). W rozważanym zagadnieniu szczególnie ważne jest pojęcie sprężystości.

Ciałem sprężystym nazywamy ciało, w którym odkształcenia, wywołane działającymi na nie siłami, zanikają zupełnie po usunięciu tych sił.Rozróżniamy kilka rodzajów odkształceń:

-odkształcenie jednostronne - siły działają na dwie przeciwległe ścianki ciała, prostopadle do nich (tak, że suma ich momentów względem dowolnego punktu ciała jest w każdej chwili równa zeru). Skutkiem działania sił jest przyrost długości (L odkształcenie bezwzględne; L/Lo odkształcenie względne ). Podczas rozciągania L > 0, a podczas ściskania L < 0.

-odkształcenie wszechstronne - na każdy element powierzchni ciała działa siła do niego prostopadła. Skutkiem działania siły jest przyrost objętości wzięty ze znakiem minus -V. Dzięki temu odkształcenie podczas ściskania ma wartość dodatnią ( Vk < Vp ).

-ścinanie - działające siły są styczne do powierzchni ciała. Miarą odkształcenia jest w tym przypadku kąt skręcenia ścianek . Wprowadzono tzw. współczynnik Poissona , który jest charakterystyczny dla danego materiału. Wyraża on stosunek względnej zmiany wymiarów poprzecznych (d/d) do względnej zmiany wymiarów podłużnych (L/L). Wartości liczby Poissona dla większości metali zmieniają się w granicach 0,2-0,5.

Naprężeniem nazywamy wektor o wartości równej stosunkowi wartości siły do powierzchni, na którą ona działa, o kierunku i zwrocie zgodnym z kierunkiem siły:

= F / S

Jednostką naprężenia w układzie SI jest : [] = N / m2 = Pa.

PRAWO HOOKE'A:

Jeżeli naprężenia w ciele są dostatecznie małe, to wywołane przez nie odkształcenia względne są do nich wprost proporcjonalne.

Odpowiednio:

L / L = * 1 / E; - V / V = * 1 / K; = * 1 / G;

gdzie:

E - moduł Younga; K - moduł ściśliwości; G - moduł sztywności.

2.Przebieg pomiarów :

*)ZESTAW POMIAROWY

-urządzenie do pomiaru wydłużenia( umocowane na stałe do ściany,z zamocowanymi dwoma mikroskopami pomiarowymi i elementem mierzonym

tzn. drutem

-przymiar liniowy (milimetrowy)

-śruba mikrometryczna

-komplet obciążników 6*1[kg] m= 0,01[kg]

*)Zestaw pomiarowy przeznaczony jest do wyznaczania przyrostów długości

drutu (zamocowanego na stałe) w celu wyznaczenia modułu Younga materia-

łu drutu metodą wydłużenia.

*)WYKONANIE POMIARÓW

**)Pomiar wielkości stałych elementu badanego

-długość początkową części pomiarowej drutu pomiędzy zamocowaniami wska-

źników mierzymy przymiarem liniowym (milimetrowym) z dokładnością do 1

[mm]

-średnicę drutu mierzymy śrubą mikrometryczną w różnych miejscach z dokła-

dnością do 0,01[mm] pomiar wykonujemy 10 razy, wyznaczamy średnią kwadratową i błąd średni kwadratowy

**)Cechowanie mikroskopów pomiarowych (odzielnie górę i dół)

-zmierzyć śednice wskaźników śrubą mikrometryczną do 0,01[mm],pomiary

wykonać 3-5 razy, wyznaczyć średniąkwadratową iśrednie błędy arytmetyczne

-zmierzyć w działkach średnice wskażników za pomocąmikroskopów pomiar powtórzyć 3-5 razy z dokładnością do pół działki wyznaczyć średnie i błędy arytmetyczne

**)Pomiar wydłużenia drutu w zależności od siły osiowej

-wyznaczyć położenia wybranych krawędzi górnego i dolnego wskaźnika dla

kolejnych wielkości obciążenia po nałożeni obciążnika wynikających z tarcia

elementów ,wykonaćpomiary dla rosnących obciążeń i dla malejących.Obliczyć wartości średnie dlatakich samych obciążeń.

Wyniki zamieszczone są w poniższych tabelkach.

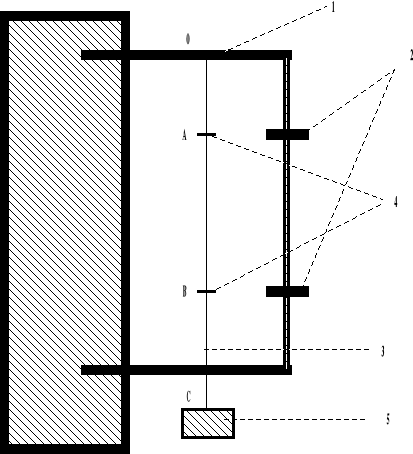
Rys.1. Urządzenie do pomiaru wydłużenia drutu.

*)Pomiar początkowej długości części pomiarowej drutu (odległość między punktem A i B).

Pomiary wykonane przyrządem milimetrowym.

|CB| = 221 mm = 1 mm

|CA| = 767 mm D= 1 mm

Lo= |CA| - |CB| = 767 - 221 = 546 mm Lo= (1 + 1) mm = 2 mm

*)Pomiary: średnicy drutu (d), średnic wskaźników punktu A i B na drucie. Pomiary zostały

wykonane śrubą mikrometryczną.

Tab. 1

nr pomiaru	di [mm]	di [mm]	WAi [mm]	WAi [mm]	WBi [mm]	WBi [mm]
1	0,85	0,016	0.59	0.002	0.70	0
2	0,85	0.,016	0.59	0.002	0.70	0
3	0,87	-0,004	0.60	-0.008	0.69	0
4	0,83	0,036	0.59	0.002	0.70	0
5	0,88	-0,014	0.59	0.002	0.70	0
6	0,88	-0,014
7	0,88	-0,014
8	0,87	-0,004
9	0,87	-0,004
10	0,88	-0,014
wart. średnia	dśr = 0,866	Ddśr = 0,0136	WAśr = 0.592	DWAśr = 0.0032	WBśr = 0.7	WBśr =0

średnica drutu: d = dśr = (0,866 0.0136) [mm]

grubość wskaźnika A: qA = WA= WAśr = (0.592 0.0032) [mm]

grubość wskaźnika B: qB = WB = WBśr = (0.7 0) [mm]

*) Pomiar grubości wskaźników za pomocą mikroskopu.

Tab 2.

wielkość mierzona	wskaźnik punktu B	wskaźnik punktu A
y - góra wskaźnika	6155	5060
x - dół wskaźnika	8330	7640
q' = (x - y) - grubość wskaźnika	2175	2580

* Wyliczenie wartości działki mikroskopu :

w= q / q' gdzie: q - grubość wskaźnika zmierzonego za pomocą śruby mikrometrycznej (wielkości: WBśr i WAśr(tabela 1))

q' - liczba działek jaką zajmuje obraz wskaźnika (tabela 2)

*) dla wskaźnika A:

w= WAśr / 2175 = 0.592 / 2175 = 2.7218E-4

[ mm / 1 działka mikroskopu ]

*)dla wskaźnika B:

w= WBśr / 2580 = 0.7 / 2580 = 2.7131E-4

[ mm / 1 działka mikroskopu ]

Przyjmuję wartość średnią:

wśr= (2.7218E-4 + 2.7131E-4) / 2 = 2.7174E-4

[ mm / 1 działka mikroskopu ]

*) Pomiar wydłużenia drutu pod wpływem obciążenia.

Tab 3.

L. p.	m	wsk. A	wsk. B	L	L	L/Lo	δ
	[ kg ]	działka mikr.	działka mikr.	działka mikr.	[ mm ]	[ - ]	[N/m*m]
1	0	5735	5070	0	0	0	0
2	1	5510	4740	105	0.0285705	5.232692E-5	16655441,55
3	2	5315	4365	285	0.0775485	1.420302E-4	33310883,09
4	3	5230	4125	440	0.119724	2.192747E-4	49966324,64
5	4	5060	3815	580	0.157818	2.89044E-4	66621766,19
6	5	4900	3465	770	0.209517	3.837308E-4	83277207,74
7	6	4745	3130	950	0.258495	4.734341E-4	99932649,28
1	5	4885	3420	800	0.21768	3.986813E-4	83277207,74
2	4	5010	3740	605	0.1646205	3.015028E-4	66621766,19
3	3	5130	4035	430	0.117003	2.142912E-4	49966324,64
4	2	5305	4320	320	0.087072	1.594725E-4	33310883,09
5	1	5470	4690	115	0.0312915	5.731044E-5	16655441,55

Gdzie:

m- masa obciążenia;

wsk. A i wsk. B - odczyt z mikroskopu położenia wskaźników;

L= (5070 - Bi) - (5735 - Ai) - bezwzględne wydłużenie drutu;

L/Lo - względne wydłużenie drutu;

= F / S = (4*m*g)/(*dśr2) - naprężenie drutu;

3.Przykładowe obliczenia:

* Wielkości przyjęte jako stałe podczas doświadczenia:

g = 9.81 [ m / s2 ]

dśr = 0.866E-3 [ m ]

  

Lo = 546 [ mm ]

wśr = 2.7174E-4 [ mm ]

* Wyliczenia wartości z tabeli 3:

- dla m= 1 kg:

L = (5070 - 4740) - (5735 - 5510) = 105 [ działek mikroskopu ]

L = 105*wśr = 105 * 2.7174E-4 = 0.0285705 [ mm ]

L/Lo = 0.0285705 / 546 = 5.232692E-5

= (4*m*g)/(*dśr2) = 16655441,55 [ N / m2 ]

* Wyliczenie modułu Young'a E

- dla przedziału m= 6 do 2 [ kg ]:

E= δ / (L/Lo) = (99932649,28-3331088,09)/(4.734341E-4 - 1.420302E-4) =

= 2,0102473 E11

- dla przedziału m=od 1 do 6[kg]

E= δ / (L/Lo) = (9,9932649,28-16655441,55)/(4.734341E-4 - 5,2322692E-5) =

= 1,97 E11

4.Dyskusja błędów :

*)błąd w wyznaczeniu długości początkowej drutu Lo (błąd = 2* działka przymiaru milimetrowego):

DLo = 2 [mm]

*)błąd w wyznaczeniu położenia A lub B (błąd przyrządu = 1 działka mikroskopu):

DA = 1

B = 1

*)błąd pomiaru średnicy d (błąd przyrządu śruby mikrometrycznej):

Dd = 0,01 [mm]

*)błąd złożony wyznaczenia L:

(L) = wśr * (a+b) = 2 * wśr

(L) = 2 * 2.7174E-4 = 5.4348E-4 [mm]

*)błąd złożony wyznaczenia modułu Younga :

E= (4*1*g* Lo)/(*dśr2*L)

Stosując metodę różniczki logarytmicznej otrzymujemy:

lnE = ln 4 + ln m + ln g + ln Lo - ln - ln( d2 ) - ln L

E / E = (0.01/6 + 0.01/9.81 + 2/546 + 0.01/3.14 + 2*0.01/0,866 + 5.4348E-4/

0,258495) =0,03473322*100%=3,47%

E = 6982236217

E = 684244384

5) WNIOSKI:

Celem doświadczenia było wyznaczenie modułu Younga. Wyznaczyliśmy wydłużenie drutu i inne dane potrzebne do obliczenia modułu Younga. Po obliczeniach otrzymaliśmy E= 2,01 E11, E=1, 97 E11 [Pa]. Błąd złożony względny w przybliżeniu wynosi 3,47 % (bezwzględny: E = 6982236217,E = 684244384). Uważam, że wynik otrzymany w naszym doświadczeniu mocno jest bliski wartości tablicowej dla stali,czy żelaza. Jednak wyznaczona wartość modułu Younga jest obarczona dużym błędem pomiarowym. Największy błąd wnosił pomiar wydłużenia L oraz średnicy drutu d. Pomiar na mikroskopach był dodatkowo utrudniony przez zmianę ostrości w okularach.

Doświadczenie potwierdza prawo Hooke'a (wykres przedstawia zależność: δf(L/L)). Doświadczenie przedstawia zjawisko sprężystości i wielkość ją charakteryzującą - moduł Younga.

Wymienione wyżej błędy mogą być spowodowane błędem paralaksy ,błędem

odzcytu, lub niedokładnością przyrządów pomiarowych.

Zależność δ  f( L/L ).

δ [ N / m * m ]

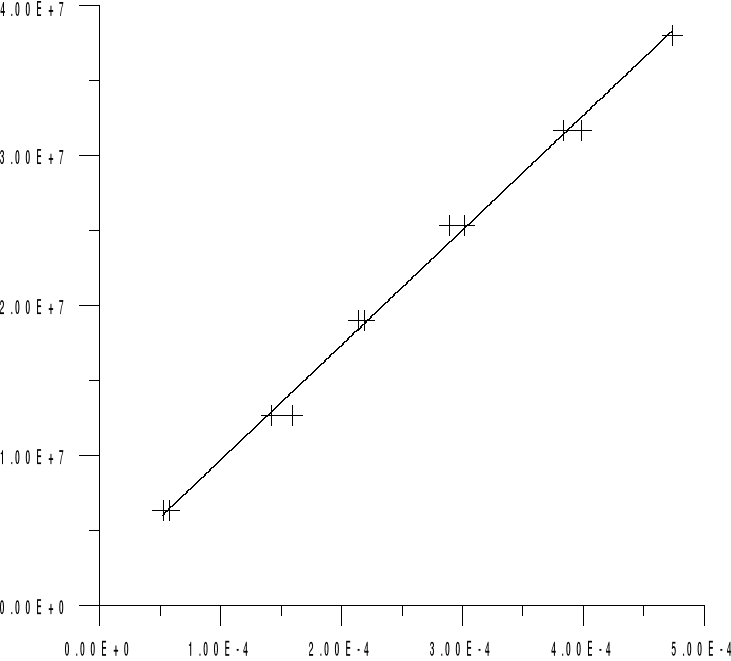
L/Lo

*) dla przedziału m= od 1 do 6 [ kg ]:

E= δ / (L/Lo) = 95648 [ MPa ]

---