Twierdzenie Cauchy'ego o wyznaczniku iloczynu macierzy)
Niech A i B będą macierzami kwadratowymi tego samego stopnia. Wtedy
![]()
.
Układem Cramera nazywamy układ równań liniowych AX = B, w którym A jest macierzą nieosobliwą.
Tw. 4.2.2 (wzór Cramera)
Układ Cramera AX = B ma dokładnie jedno rozwiąznie. Rozwiązanie to jest określone wzorem
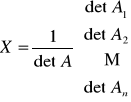
,
gdzie n oznacza stopień macierzy A, natomiast Aj, dla 1 ≤ j ≤ n, oznacza macierz A, w której j-tą kolumnę zastąpiono kolumną wyrazów wolnych B, tzn.
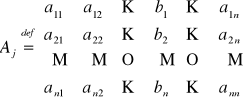
.
Uwaga. Równość określającą rozwiązanie układu równań liniowych nazywamy wzorem Cramera. Równość ta po rozpisaniu przyjmuje postać:
![]()
, ![]()
, …, ![]()
,
zwaną wzorami Cramera.
Fakt 4.2.3 (metoda macierzy odwrotnej)
Rozwiązanie układu Cramera AX = B jest określone wzorem: ![]()
.
Ortogonalizacja Grama-Schmidta to metoda za pomocą której można przekształcić zbiór liniowo niezależnych wektorów przestrzeni unitarnej w zbiór wektorów ortogonalnych. Przestrzenie liniowe, rozpinane przez zbiory przed i po ortogonalizacji są tożsame, tak więc proces może służyć do ortogonalizowania bazy.
Operator rzutowania ortogonalnego wektora v na wektor u definiujemy jako:
Wówczas dla układu k wektorów{v1, …, vk} proces przebiega następująco:
Dwa pierwsze kroki procesu ortogonalizacji
Otrzymany zbiór {u1, …, uk} jest zbiorem wektorów ortogonalnych.
Proces ortogonalizacji pozwala na wskazanie bazy ortogonalnej w dowolnej n-wymiarowej przestrzeni unitarnej. Jej istnienie można wykazać na bazie lematu Kuratowskiego-Zorna.
(iloczyn skalarny)
Niech ![]()
będą dowolnymi wektorami w R3. Iloczyn skalarny wektorów ![]()
i ![]()
określamy wzorem:
![]()
,
gdzie ϕ jest miarą kąta między wektorami ![]()
i ![]()
Uwaga. Miara kąta między wektorami niezerowymi ![]()
i ![]()
wyraża się wzorem:
![]()
.
Rzut prostopadły wektora ![]()
na wektor ![]()
wyraża się wzorem:
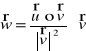
.
Fakt 5.2.2 (wzór do obliczania iloczynu skalarnego)
Niech ![]()
oraz ![]()
będą wektorami w R3. Wtedy
![]()
Fakt 5.2.3 (własności iloczynu skalarnego)
Niech ![]()
będą dowolnymi wektorami w R3 oraz niech α ∈ R. Wtedy
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
wektory ![]()
i ![]()
są prostopadłe ⇔ ![]()
.
Uwaga. Równość podana w punkcie 3 jest prawdziwa także dla dowolnej liczby wektorów składników. Równość w nierówności 5 jest możliwa tylko wtedy, gdy wektory ![]()
i ![]()
są równoległe.
Wyszukiwarka
Podobne podstrony:
Macierze - ściąga, Analiza matematyczna
Geometria analityczna - ściąga, Analiza matematyczna
Elementy przebiegu zmienności funkcji. Twierdzenie de l’Hospitala, Analiza matematyczna
sciaga analiza, MATEMATYKA(1)
Analiza matematyczna 2 - ściąga, Analiza matematyczna studia, analiza matematyczna, analiza matematy
Analiza Matematyczna Twierdzenia
Analiza matematyczna 2 ściąga
sciaga kolo1 analiza fin, WTD, analiza matematyczna
Analiza matematyczna 2 Definicje, twierdzenia, wzory
ANALIZA MATEMATYCZNA - ściąga, Edukacja, Analiza matematyczna
Analiza matematyczna Teoria sciaga
ANALIZA MATEMATYCZNA sciaga kolo 2
Analiza matematyczna twierdzenia
analiza sciaga, studia, Matma, Analiza Matematyczna, analiza, Ściągi
Analiza matematyczna, Analiza matematyczna - wykład, Ściąga z wykładów
Analiza matematyczna 2 Definicje, twierdzenia, wzory (2)
więcej podobnych podstron